aula funcoes1

Responsáveis: Acadêmicos Bruno Bastos Braga, Bruno Silveira Correa, Roger Martins; Profa. Fabiana F. Serres, Prof.
Marcus Vinicius de A. Basso.
Revisão de Funções
Def.1.1: Funções: dados dois conjuntos A e B, não vazio, uma função de A
em B é uma regra que diz como associar cada elemento x
A a um único
elemento y
B.
Usamos a seguinte notação:
Lê-se: f é uma função de A em B.
Ex:
A função f transforma x de A em y de B. Denotamos isso assim:
Def.1.2: Domínio e imagem: Dada uma função f de A em B, o conjunto A
chama-se domínio da função, indicado por
. Para cada x A, o elemento y
B chama-se imagem de x pela função f ou o valor assumido pela função f
para x
A e o representamos por
(lê-se: f de x). Assim,
, como
na figura acima. O conjunto de todos os y assim obtidos é chamado conjunto
imagem da função f e é indicado por
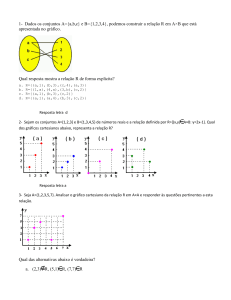
Ex: Dados os conjuntos A={1,2,3} e B={1,2,3,4,5,6,7} vamos considerar
a função
, que transforma todo x A em 2x B.
O domínio é A,
.
A o conjunto imagem é:
.
Def.1.3: Funções definidas por fórmulas matemática: No exemplo anterior
vimos que todo x A levava a 2x B. Podemos interpretar da seguinte forma:
ou
Outros exemplos:
ou
ou
ou
Def.1.4: Coordenadas cartesianas: A notação (a,b) é usada para indicar o par
ordenado de números reais a e b, no qual o número a é a primeira coordenada
e o número b é a segunda. Observe que os pares ordenados (4,3) e (3,4) são
diferentes, pois as coordenadas são diferentes.
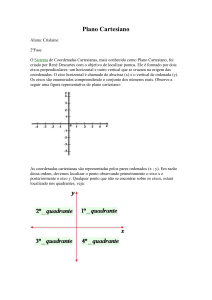
Def.1.5: Sistema de eixos ortogonais: Um sistema de eixos ortogonais é
constituído por dois eixos perpendiculares, 0x e 0y, que têm a mesma origem.
Damos o nome de plano cartesiano a um plano com um sistema de
eixos ortogonais.
Os eixos ortogonais dividem o plano cartesiano em quatro regiões
chamadas quadrantes na seguinte ordem:
Usamos esse sistema para localizar pontos no plano. Dado um ponto P
desse plano, dizemos que os números a e b são as coordenadas cartesianas
do ponto P, em que a é a abscissa e b a ordenada.
Por exemplo, vamos localizar no plano cartesiano os pontos A(4,1),
B(1,4), C(-2,-3), D(2,-2), E(-1,0), F(0,3) e O(0,0).
Construção de gráficos de funções
Para construir o gráfico de uma função dada por
,
, no plano cartesiano, devemos:
1) Construir uma tabela com valores de x escolhidos convenientemente
no domínio D e com valores correspondentes para
;
2) A cada par ordenado (x,y) da tabela associar um ponto do plano
cartesiano;
3) Marcar um número suficiente de pontos, até que seja possível
esboçar o gráfico da função.
Por exemplo, vamos construir o gráfico da função
:
Determinando o domínio e a imagem de uma função, a partir do gráfico
Observando o gráfico de uma função no plano cartesiano podemos, às
vezes, determinar o domínio D e a imagem Im de uma função, projetando o
gráfico nos eixos. Ex: