FUNÇÕES
Ao lermos um jornal ou uma revista, diariamente nos deparamos com gráficos, tabelas e
ilustrações. Estes, são instrumentos muito utilizados nos meios de comunicação. Um texto com
ilustrações, é muito mais interessante, chamativo, agradável e de fácil compreensão. Não é só nos
jornais ou revistas que encontramos gráficos. Os gráficos estão presentes nos exames laboratoriais, nos
rótulos de produtos alimentícios, nas informações de composição química de cosméticos, nas bulas de
remédios, nos relatórios das empresas, enfim em todos os lugares.
Ao relacionarmos espaço em função do tempo, número do sapato em função do tamanho
dos pés, intensidade da fotossíntese realizada por uma planta em função da intensidade de luz a que ela
é exposta ou pessoa em função da impressão digital, lucros e investimentos de uma empresa, horas de
funcionamento de uma máquina e consumo de energia percebemos quão importantes são os conceitos
de funções para compreendermos as relações entre os fenômenos físicos, biológicos, sociais...
O Plano Cartesiano
O plano cartesiano ortogonal é constituído por dois eixos x e y perpendiculares entre si que
se cruzam na origem. O eixo horizontal é o eixo das abscissas (eixo OX) e o eixo vertical é o eixo das
ordenadas (eixo OY). Associando a cada um dos eixos o conjunto de todos os números reais, obtém-se
o plano cartesiano ortogonal.
Cada ponto P = (a,b) do plano cartesiano é formado por um par ordenado de números,
indicados entre parênteses, a abscissa e a ordenada respectivamente. Este par ordenado representa as
coordenadas de um ponto.
Produto Cartesiano
Dados dois conjuntos A e B não vazios, definimos o produto cartesiano entre A e B,
denotado por AxB, como o conjunto de todos os pares ordenados da forma (x,y) onde x pertence ao
primeiro conjunto A e y pertence ao segundo conjunto B.
AxB = { (x,y): x A e y B }
Observe que AxB BxA, se A é não vazio ou B é não vazio. Se A=Ø ou B=Ø, por
1
definição: AxØ = Ø = Ø x B.
Ex: Dados A={a,b,c,d} e B={1,2,3}, o produto cartesiano AxB, terá 12 pares ordenados e será dado
por:
AxB= {
FUNÇÕES
Dados dois conjuntos, A e B, não-vazios, dizemos que a relação f de A em B é função
se, e somente se, para qualquer x pertencente ao conjunto A, existe, em correspondência, um único y
pertencente a B, tal que o par ordenado (x, y) pertença a f.
Simbolicamente:
f é função de A em B ( x A, y B| (x, y) f)
Exemplo:
Dados os conjuntos A = { -1, 0, 1, 2, 3} e B = { 0, 1, 2, 3, 4}, vamos analisar algumas
relações estabelecidas a partir de A x B e determinar quais são funções e quais não são:
a) R1 = { (x, y) A x B | y = x2 }
-
Determinação de seus elementos:
- Representação:
Conclusão: _____________________________________________________________________
b) R2 = { (x, y) A x B | y = x + 1 }
-
Determinação de seus elementos:
- Representação:
- Conclusão: __________________________________________________________________
R3 = { (x, y) A x B | y = 5 }
-
Determinação de seus elementos:
- Representação:
-
Conclusão: __________________________________________________________________
2
EXERCÍCIOS PROPOSTOS:
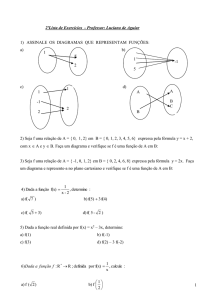
1) ASSINALE OS DIAGRAMAS QUE REPRESENTAM FUNÇÕES:
a)
b)
1
1
2
3
c)
1
5
0
1
-1
9
d)
8A
B
C
-1
2
A
2
B
D
-2
3
3
B
2) Seja f uma relação de A = { 0, 1, 2} em B = { 0, 1, 2, 3, 4, 5, 6} expressa pela fórmula y = x + 2,
-3
com x A e y B. Faça um diagrama e represente-a no plano cartesiano e verifique se f é uma função
de A em B:
3) Seja f uma relação de A = { -1, 0, 1, 2} em B = { 0, 2, 4, 6, 8} expressa pela fórmula y = 2x. Faça
um diagrama e represente-a no plano cartesiano e verifique se f é uma função de A em B:
4) Dados A = { -2, -1, 1, 2} e B = { -8, -4, -1, 0, 1, 4, 8}, e uma relação f de A em B expressa pela
fórmula y = x3, com x A e y B. Faça um diagrama e represente-a no plano cartesiano e verifique
se f é uma função de A em B:
Valor Numérico De Uma Função:
Dados os conjuntos A = {-2, -1, 0} e B } { 0, 1, 2} e a função f: A B, definida por
f(x) = x + 2, chamamos de valor numérico da função f(x) o valor que a variável y assume quando a
variável x é substituída por um determinado valor que lhe é atribuído.
Exemplo:
Dada a função f(x) x2 – x + 2, atribuindo valores a x, obtemos:
- para x = 2
f(x) =
3
- para x = - 1
f(x) =
EXERCÍCIOS PROPOSTOS:
1
1
)Dada
a
função
f(x)
,determine
:
x
-2
a)
f(
7
)
b)
f(5)
3
f(4)
c)
f(3
3)
d)
f(
5
-2
)
2) Dada a função real definida por f(x) = x2 – 3x, determine:
a) f(1)
b) f(-1)
c) f(3)
d) f(2) – 3 f(-2)
1
*
3
)
Dada
a
função
f:
R
R
;definida
por
f(x)
,calcule
:
x
a)
f(2
)
1
b)
f
2
4) Dada a função real f(x) = - x2 + x :
a) calcule f(0)
b) calcule x, tal que f(x) = 0:
5) Dadas as funções f: R* R, tal que f(x) = 2x2- 3x + 1, determine f(x + 1):
6) Dada a função f: R R, tal que f(x) = 2 – x, calcule x para que f(x) = 3:
7) Os calçados são medidos por números: 35, 36 e 37 para a maioria das mulheres e 38, 40 e 41 para
a maioria dos homens. O número y do sapato depende do comprimento x (em cm) do pé, e a fórmula
para calcular y é: y = (5x + 28) / 4. Com base nessa relação, responda:
a) Que número calça uma pessoa cujo pé mede 24,8 cm?
b) Que número calça uma pessoa cujo pé mede 20 cm?
c) Quanto mede o comprimento de um pé que calça 42?
Domínio, Imagem E Contradomínio
DOMÍNIO de uma função f (D(f)) é o conjunto formado pelos primeiros elementos dos pares
ordenados (x, y) pertencentes a f.
Pela definição de função, todos os elementos de A têm um único correspondente em B; logo, o
4
domínio de f sempre é o conjunto A .
IMAGEM de uma função f(Im(f)) é o conjunto formado pelos segundos elementos dos pares
ordenados (x, y) pertencentes a f.
Im (f) B
CONTRADOMÍNIO é o conjunto B.
Exemplo:
1) Dados os conjuntos A = { -2, -1, 0, 1} e B = {-2, -1, 0, 1, 2, 3} e a função f: A B, definida por
f(x) = x + 1, determine:
D(f) =
Im(f) =
Cd(f) =
EXERCÍCIOS PROPOSTOS:
1) Considerando o diagrama seguinte, que representa uma função de A em B, determine o que se
pede:
-1
0
a) D
b) f(-1)
1
1
c) f(0)
0
2
d) f(1)
3
e) Im
f) CD
2
4
2
2
)
Determine
o
conjunto
imagem
da
função
:
f
:
{-2,
0,
2
}
R
defin
por
f(x)
3
x
:
3) Seja f uma relação de A = { -4, -3, -2, -1, 0} em B = { -3, -2, -1, 0, 2, 3, 4, 5} definida por
f(x) = 2x + 5. Fazendo o diagrama de f, verifique se f é uma função de A em B e, em caso afirmativo,
determine o conjunto imagem:
Gráfico De Uma Função:
Para esboçarmos o gráfico de uma função no plano cartesiano, devemos atribuir alguns valores
à variável x, determinando valores numéricos de y.
Exemplos:
5
1) Sendo E = {-2, -1, 0, 1, 2} e F = {0, 1, 2}, esboçar o gráfico da função y = |x|:
2) Dados G = [-2, 2] e H = [-4, 4], esboçar o gráfico da função f(x) = 2x:
3) Construir no plano cartesiano o gráfico da função f: R R definida por y = 2x – 1.
2
x
4
)
Construir,
no
plano
cartesiano
,
o
gráfico
da
função
f(x)
:
2
x,
se
x
2
5
)
Construir
no
plano
catesiano
o
gráficoda
função
f
:
R
R
definida
por
f(x)
2,
se
x
2
Gráficos Fundamentais
6
EXERCÍCIOS PROPOSTOS:
1) Esboce o gráfico da função f: A B definida, por f(x) = x2, sendo A = { -1, 0, 1, 2} e B = {0, 1, 2,4}:
2) Represente graficamente as funções dadas por:
b) y = 3 – 2x, x [-3, 4]
a) y = -x
c) y = x2+ 1 , x 0
3) Construa num sistema de coordenadas cartesianas o gráfico:
a) da função f: R R dada por f(x) = x + 1
b) da função f: R R dada por f(x) = x – 1
Nos dois exercícios, escreva o domínio D e o conjunto imagem Im da função:
4) Construa num sistema de coordenadas cartesianas ortogonais o gráfico:
a) da função dada por f(x) = x2 + 3
b)
da função dada por f(x) = 2x
Nos dois exercícios, escreva o domínio D e o conjunto imagem Im da função:
5) Construa num gráfico de coordenadas cartesianas o gráfico da função f: R R definida por:
x
-1,
se
x
1
f(x)
0,se
x
1
6) Faça o gráfico da função definida por:
x2,sex0
sex0
x,
COMPOSIÇÃO DE FUNÇÕES
A função composta g[h(x)] é a função formada pelas duas funções g(u) e h(x), substituindo-se u
por h(x) na fórmula de g(u).
Exemplo:
Determine a função composta g[h(x)], se g (u) = u2 + 3 u + 1 e h(x) = x + 1:
EXERCÍCIOS PROPOSTOS:
1) CALCULE A FUNÇÃO COMPOSTA g [h(x)]:
a) g(u) = u2 + 4 ; h(x) = x – 1
c) g(u) = (2u + 10)2; h(x) = x – 5
b) g(u) = 3 u2 + 2u – 6 ; h(x) = x + 2
1
2
d)
g(u)
,h(x)
x
x
2
u
2) Usando g(u) = u2 + 3 ; h(x) = x – 2 , verifique se a composição de funções é comutativa:
7
FUNÇÕES INVERSAS
Duas funções, f e g, são inversas uma da outra se: f(g(x)) =m x para cada x no domínio de g e g(f(x))
= x para cada x no domínio de f. A função g se representa por f -1 , que se lê como “inversa de f”. Parta
que f e g sejam inversas uma da outra, a imagem de g deve ser igual ao domínio de f, e vice-versa.
Exemplo:
1) DETERMINE A INVERSA DE f(x): ( se houver):
a) f(x) = 2x
b) f(x) = x2 + 1
EXERCÍCIOS PROPOSTOS:
1) DETERMINE A INVERSA DE f(x): ( se houver)
a) f(x) = 3x – 1
b) f(x) = 2 - x2
c) f(x) = 2x + 3
2) PARA CADA item, calcule: f + g, f – g, f . g, f g, f o g, f-1:
a) f(x) 3x , g(x) = x2+ 1
x
1
b)f(x)
2e
g(x)
1
x
x
PROPRIEDADES DAS FUNÇÕES
FUNÇÃO SOBREJETIVA (SOBREJETORA): Uma função f: S R T é uma função sobrejetiva se a
imagem de f(f(S)) é igual ao contradomínio de f(T).
Exemplo:
FUNÇÃO INJETIVA (INJETORA): Uma função f: S R T é injetiva ou um-para-um se nenhum
elemento de T for imagem de dois elementos distintos de S.
Exemplo:
FUNÇÃO BIJETIVA (BIJETORA):Uma função f: S R T é bijetora se for, ao mesmo tempo, injetiva e
sobrejetiva.
Exemplo:
8
EXERCÍCISO PROPOSTOS:
1) DETERMINE SE AS FUNÇÕES ABAIXO SÃO INJETORAS, SOBREJETORAS OU
BIJETORAS; JUSTIFICANDO:
A)
B)
C)
D)
2) Dados os conjuntos A = { -2, -1, 0, 1} e B = {-2, -1, 0, 1, 2, 3} e a função f: A B, definida por
f(x) = x + 2,determine: D(f) , Im(f) e Cd(f). Verifique se a função é injetora, sobrejetora ou bijetora:
3) Verificar se f:R
R, definida por f(x)=3x+2, é bijetora. Justifique:
4) Construa um exemplo de função que não seja nem injetora, nem sobrejetora:
4) ANALISE o gráfico e responda:
a) Que tipo de função está representada? Justifique:
b) Qual é a raiz da função? Justifique:
c) Qual é a imagem de x = 2 e x = 0?
9