Relações métricas no tri.retângulo.

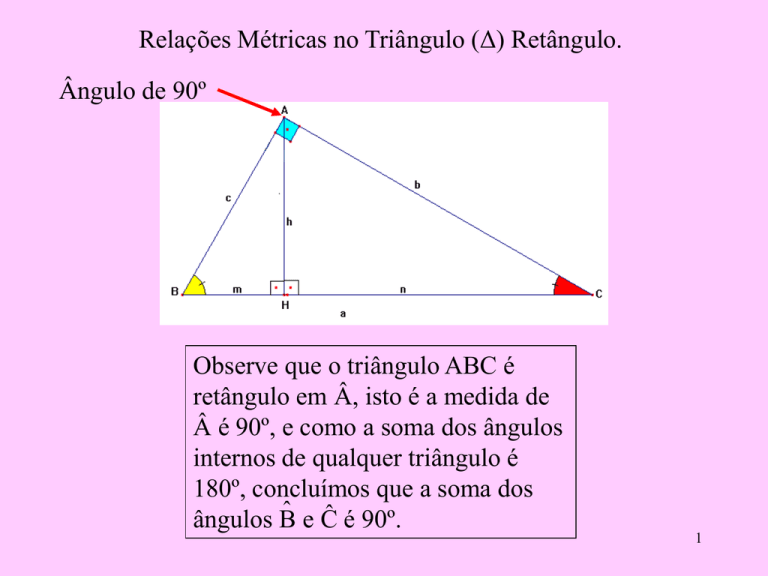
Relações Métricas no Triângulo (Δ) Retângulo.
Ângulo de 90º
Observe que o triângulo ABC é
retângulo em Â, isto é a medida de
 é 90º, e como a soma dos ângulos
internos de qualquer triângulo é
180º, concluímos que a soma dos
ˆ e Ĉ é 90º.
ângulos B
1
Ao dividirmos o triângulo ABC,
pela altura relativa a sua hipotenusa,
formamos os triângulos ABH e
ACH, veja que são retângulos em
Ĥ. E assim, desta forma verificamos
que acabamos por dividir o ângulo
 nos dois ângulos já conhecidos
ˆ
do triângulo ABC que são Ĉ e B.
Quando dois triângulos,
possuírem ao menos dois
ângulos de mesma
medida, significa que
são semelhantes.
2
Observem agora os lados deste triângulo.
Ângulo de 90º
Lado AC
Lado AB
Lado BC
O lado AB “ vai do ângulo de 90º até o ângulo pintado de amarelo”.
O lado BC “ vai do ângulo pintado de amarelo até o ângulo pintado de
vermelho”.
O lado AC “ vai do ângulo de 90º até o ângulo pintado de vermelho”.
3
Observe que dividimos o triângulo ABC em dois
novos triângulos ABH e ACH, que são semelhantes
entre si, pois seus ângulos são congruentes “iguais” e
seus lados são proporcionais.
4
Vamos agora comparar o triângulo ABC com o triângulo ABH.
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:
a
b
c


c
h
m
Lados do Δ ABC
Lados do Δ ABH
5
a

c
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABC e ABH.
b
c

h
m
Não se esqueça que: “para passar o número que esta
dividindo para o outro lado do sinal de igual o
fazemos passar, multiplicando do outro lado”.
Deduzimos as seguintes relações:
1ª)
ah = cb
2ª) bm = ch
3ª)
cc = am
6
Comparando o triângulo ABC com o triângulo ACH.
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:
b
c
a


n
h
b
Lados do Δ ABC
Lados do Δ ACH
7
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABC e ACH.
Deduzimos as seguintes relações:
b
c
a


n
h
b
1ª) bh = cn
2ª) bb = an
3ª) bc = ah
8
Comparando o triângulo ABH com o triângulo ACH.
Como são semelhantes, seus lados são proporcionais, logo temos
as seguintes relações:
c
h
m


b
n
h
Lados do Δ ABH
Lados do Δ ACH
9
Das proporções obtidas dos lados dos
Δs semelhantes que são:ABH e ACH.
Deduzimos as seguintes relações:
c
h
m


b
n
h
1ª) bh = cn
2ª) ch = bm
3ª) hh = mn
10
Outra relação métrica é: a = m + n, ou seja
m (segmento BH) é a projeção do cateto c
sobre a hipotenusa e n (segmento CH) é a
projeção do cateto b sobre a hipotenusa, logo
a soma de m (BH) + n (CH) é igual a
hipotenusa a (segmento BC).
Imagine estas
projeções sendo
como o sol
“batendo”numa
ripa de madeira
inclinada numa
parede, isto
produz uma
sombra, a qual
chamaremos de
projeção.
11
Ângulo de 90º
Teorema de Pitágoras
Cateto
Cateto
Hipotenusa
O lado BC do Δ ABC é contrário (está de frente) com o ângulo de
90º, por esse motivo leva o nome especial de Hipotenusa.
Os lados AB e AC do Δ ABC são chamados de Catetos.
12
Temos a relação: hipotenusa ao quadrado é igual a
soma dos quadrados dos catetos.
Hip2 = cat2 + cat2
a 2 = b2 + c 2
Teorema de Pitágoras.
13
Resumo das fórmulas das relações
métricas no Δ retângulo.
1ª) ah = bc
4ª) bh = cn
7ª) a = m + n
2ª) c2 = am
5ª) b2 = an
8ª) a2 = b2 + c2
3ª) bm = ch
6ª) h2 = mn
14
Espero que tenham gostado da aula em slides:
Autor: Prof. Jose Fabio Braga Szmelcynger.
E-mail: [email protected] - fone 0xx1938079073
Data: 22/02/2004.
Amparo-SP.
15