Teste-1_outubro2009_v1_Correcção

Correcção da 1ª Ficha de Avaliação de Matemática
Outubro de 2009 10ºA – versão 1
Grupo I
1. Uma vez que por definição um radiano é a amplitude de um arco cujo comprimento é
igual ao raio, a resposta certa é (B).
2. Sendo x um ângulo do primeiro quadrante, cos x  0 e uma vez que
 3

sen
 x    cos x , a resposta certa é (D).
 2


 3

 3

   ; sen
    que simplificando
 2

 2

3. As coordenadas do ponto B são  cos

são  sen , cos   , logo a resposta certa é (A).
4. A afirmação A é verdadeira uma vez que o cosseno e a tangente são ambos negativos
no 2ºQ logo o seu produto é positivo.
A afirmação B é falsa pois no 3ºquadrante o seno e o cosseno são ambos negativos.
A afirmação C é falsa porque  1  cos( x)  1 , x  R
A afirmação D é falsa pois no 1ºQ a tangente toma todos os valores positivos.


5.  5  5sen 2 x  5  1  sen 2 x  5( cos 2 x)  5 cos 2 x Resposta (B)
Grupo II
y
1. 1.1 Reparar que se sen  
3


     então  é um
4
2
2
ângulo de amplitude negativa.
1.2 Recorrendo à fórmula fundamental da trigonometria,
2
 3
2
    cos   1 
 4
7
7
. Como   4º Q, cos  
4
4
3

sen
3
tg 
 tg  4  tg  
cos 
7
7
4
 3 
1.3 Fazendo tg 1  
  0,8 e como
7

 cos   


2
 

2
, concluímos que   0,8 rad
x
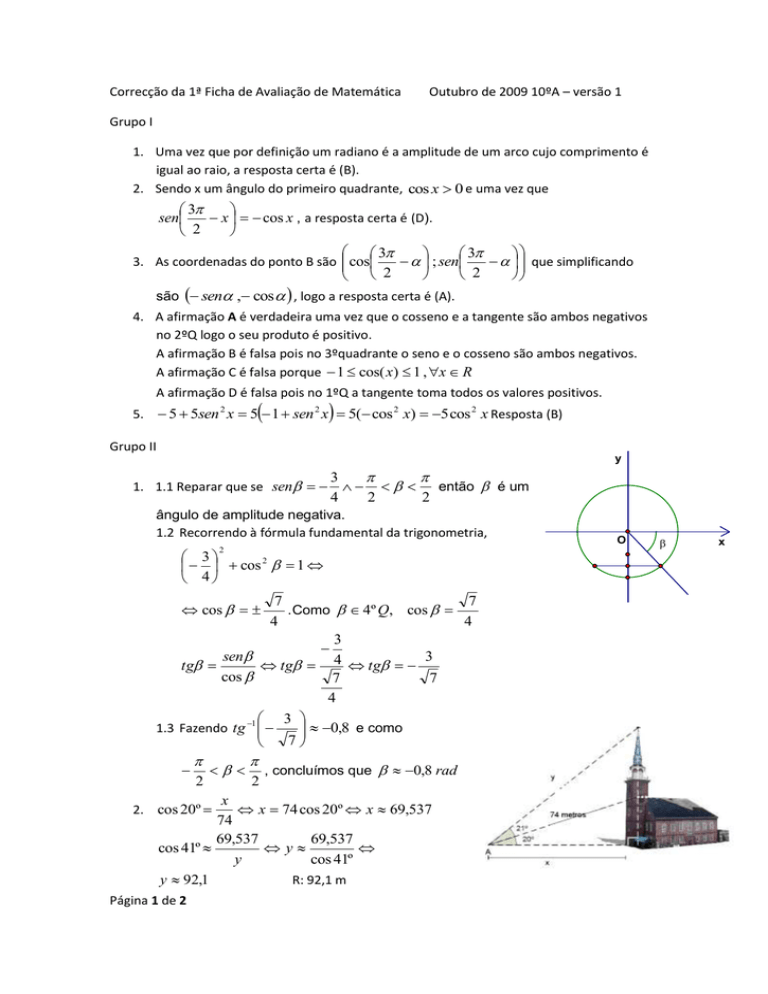
 x  74 cos 20º  x  69,537
74
69,537
69,537
cos 41º 
y

y
cos 41º
y  92,1
R: 92,1 m
2. cos 20º 
Página 1 de 2
O

x
1
cos(300º )  tg (135º )  sen 90 
2
1
 2sen(4  360º 120º )  cos(360º 60º )  tg (180º 45º )  (1) 
2
1
1
 2sen(120º )  cos( 60º )  tg (45º )  1  2sen(180º 60º )  cos(60º )  1  1 
2
2
3. 3.1 2sen(1560º ) 
1 1
3 1 4 3 1
 2sen(60º )    2 
 
2 2
2 4
4
 13 
 2 
 3 
  cos
  tg 
  cos 3  
 6 
 3 
 4 
3.2 4sen






 4sen 2    cos     tg      cos   
6
3
4



1 1
1
  
  
 
 4sen     cos    tg   (1)  4    1  1 
2 2
2
6 
 3 
4
4. 4.1
1

 3



f ( x)  cos   x   2sen
 x   3 cos(  x)  sen 2   x    1 
2
2
 2



1


 f ( x)   cos x   2   cos x   3 cos( x)  sen  x   1 
2
2

1
3
 f ( x)   cosx   2 cos x  3 cos( x)  cos x  1  f ( x)   cos( x)  1
2
2
 1  cos( x)  1 , x  R 
4.2
3 3
3
3
3
3
 cos( x)  , x  R    cos( x)   , x  R 
2 2
2
2
2
2
3
3
3
1
5
  1   cos( x)  1    1 , x  R   f ( x)   , x  R
2
2
2
2
2
 5 1
y
D f   ; 
 2 2
B
A

5.
A
DC  AB
 BP
2
BP
sen 
 BP  sen
1
Então
A( ) 

D
P
C
x
OP
cos  
 OP  cos 
1
2  2 cos 
21  cos  
 sen  A( ) 
 sen  A( )  1  cos    sen 
2
2
 A   sen  cos   sen c.q.d.
Página 2 de 2
O