"2 1" soma -seu 1

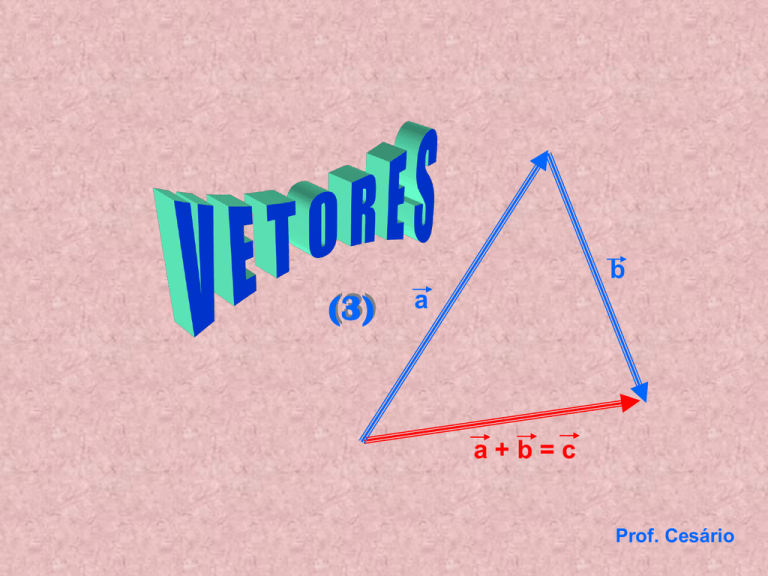
b
(3)
a
a+b=c
Prof. Cesário
8 – OPERAÇÕES USANDO AS COMPONENTES
Sejam v1 = x1i + y1j +z1k e v2 = x2i + y2j + z2k dois vetores.
Atenção: a partir deste ponto usaremos a notação negrito-itálico para
indicar uma grandeza vetorial. Isto é: a notação negrito-itálico
substituirá a seta em cima da letra.
(i) ADIÇÃO
v1 + v2 = (x1 + x2)i + (y1 + y2)j + (z1 + z2)k
Soma dos x, soma dos y, soma dos z.
(ii) MULTIPLICAÇÃO POR ESCALAR
r.v1 = (rx1)i + (ry1)j + (rz1)k
Multiplica-se o escalar “r” por cada uma das coordenadas.
(iii) SUBTRAÇÃO
v1 – v2 = (x1 – x2)i + (y1 – y2)j + (z1 – z2)k.
Subtrai-se as coordenadas.
(iv) PRODUTOS
Existem grandezas que, apesar de serem escalares, são definidas
a partir de um produto de dois vetores. Como exemplo temos a grandeza
trabalho que é definida como um produto do vetor deslocamento pelo
Vetor força.
Outras, também definidas, como um produto de dois vetores são
grandezas vetoriais. É o caso de uma força sobre uma partícula
eletrizada em movimento em um campo magnético.
Vejamos esses dois tipos de produto.
9 – PRODUTO ESCALAR
Dados dois vetores u e v, define-se o produto escalar de u por v, denotado
u.v, como sendo o escalar:
u.v = |u|.|v|.cos 
Onde |u|, |v| são os módulos dos vetores u e v e
 o ângulo por eles formados.
Lembrete:
Se os vetores forem indicados na
Para indicar um vetor
forma xi + yj + zk, ao multiplicar,
estamos usando as
teremos produtos obtidos a partir
letras em negrito-itálico.
dos unitários i, j, k.
i.i = j.j = k.k = 1.1.cos 0º = 1.1.1 = 1
i.j = i.k = j.i = j.k = k.j= k.i = 1.1.cos 90º = 1.1.0 = 0
Assim,
(x1i + y1j + z1k) . (x2i + y2j + z2k) =
x1.x2 + y1.y2 + z1.z2
Exemplo 1: Se u = 3i + 4j – 6k e v = 5i + 5j + 2 k,
u.v = 3.5 + 4.5 + (-6).2 = 23
Exemplo 2:
O trabalho é definido pelo produto escalar r.F onde r é o vetor deslocamento
e F é a força.
Determinar o trabalho realizado pela força F = 20i + 12j – 5k (N) enquanto o
corpo se desloca do ponto A = (1, 2, 0) ao ponto (5, 4, 3) (coordenadas dadas
em metros).
O vetor r vai do ponto (1, 2, 0) ao ponto (5, 4, 3). Isto significa
5 – 1 = 4 unidades para a direita;
4 – 2 = 2 unidades para cima;
3 – 0 = 3 unidades para fora.
Portanto: r = 4i + 2j + 3k.
W = r.F = (20.4) + (12.2) + (-5.3) = 89 joules
10 – PRODUTO VETORIAL
Dados os vetores u e v, define-se o produto vetorial, que é indicado
por u X v ou u  v como sendo o vetor w com as seguintes
características:
(i) Módulo de w:
|w| = |u| . |v| . sen 
Onde  é o ângulo formado pelos dois vetores.
(ii) Direção de w: perpendicular ao plano formado por u e v.
(iii) Sentido de w: determinado pela regra da mão direita aberta
(regra do tapa)
Com a mão direita aberta:
Os demais dedos
apontam o sentido
do segundo vetor.
Aponta com o polegar o primeiro
vetor
A palma da mão indicará o produto.
APLICAÇÕES FÍSICAS DO PRODUTO VETORIAL
Se você aplica a força F, a porca terá o
(1) TORQUE

Pode-se aplicar a força F à distância r ou
a força 2F à distância r/2, para produzir
o mesmo efeito.
r
F
movimento indicado pelo vetor  que
é denominado torque.
F
O efeito de rotação devido a força é denominado
Torque.
Se P é o ponto de aplicação da força e O o centro de rotação, o torque
da força F em relação ao ponto O é definido por

= AO X F
(2) MOVIMENTO DE CARGA ELÉTRICA EM CAMPO MAGNÉTICO
F
S
B
Q
ímãs
N
Os ímãs criam um campo magnético.
v
Se uma partícula atravessa um campo
magnético ela sofre a ação de uma força.
A força que age sobre a partícula
eletrizada tem o sentido indicado é dada por
F = q.v X B
EXERCÍCIOS
1 – Dados os vetores abaixo, decomponha-os e determine o módulo e a
orientação do vetor soma ou resultante:
v1 = 300 m, S40ºL; v2 = 200 m, O30ºN; v3 = 200 m, L40ºS;
v4 = 500 m, N60ºL.
2 - Determine a soma dos vetores indicados
na figura (I).
3 - Sejam u = (1, 2, 3), v = (-4, 8, -3) e
w = (4, -2, -1) três vetores. Calcule:
(a)u.v
(b)uxw
( c ) (u . v) . w
( d ) u x (v . w)
( e ) (u x v) . w
( f ) 2u x 3w
( g ) u . 2w + 3u . 4v
( h ) u x (w x v)
( i ) (u x w) x v
( j ) 2u . 3w
( k ) u . (v . w)
( l ) u x (v . w)
Observação: a notação (1, 2, 3) é equivalente a
1i + 2j + 3k.