Aula 5-ICs

Aula 5. Intervalos de Confiança
Métodos Estadísticos 2008
Universidade de Averio
Profª Gladys Castillo Jordán
Duas Fases da Estatística


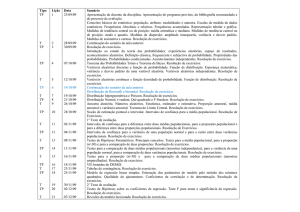
Estatística Descritiva: descrever e estudar uma amostra
Estatística Indutiva (inferencial): a partir de uma
amostra inferir sobre as características de uma
população
Fonte Diagrama: Projecto ALEA – Noçoes de Estatística
http://alea-estp.ine.pt/Html/nocoes/html/exemplo2_4_1_11.html
2
População vs. Amostra
Podemos inferir (deduzir) determinadas características de uma
população se extraímos uma amostra representativa desta
Amostra: Conjunto de dados ou
observações, recolhidos a partir de
um subconjunto da população, que
se estuda com o objectivo de tirar
conclusões para a população de
onde foi recolhida
População: colecção de unidades
individuais (pessoas ou resultados
experimentais) com uma ou mais
características comuns, que se
pretendem estudar.
amostragem
Imagens extraídas da referência 2
3
Amostragem
Processo pelo qual se extraem dados de uma população
Existem vários tipos de amostragem:

Vamos usar apenas este tipo
Amostragem Aleatória Simples: cada elemento da amostra é retirado
aleatoriamente de toda a população (com ou sem reposição)
 cada possível amostra tem a mesma probabilidade de ser recolhida

Amostragem Estratificada: subdividir a população em, pelo menos,
dois subgrupos distintos que partilham alguma característica e, em
seguida, recolher uma amostra de cada um dos subgrupos (estratos)

Amostragem por clusters: dividir a população em secções (clusters);
seleccionar aleatoriamente alguns desses clusters; escolher todos os
membros dos clusters seleccionados.
4
Inferência Estatística
inferir certas características
n indivíduos (ou objetos) da população
da população
ex: sortear n pixels de uma imagem
(com ou sem reposição)
amostra
n realizações de uma v.a. X
ex: medir a reflectância de um objeto
n vezes

distribuição conhecida/desconhecida
e/ou parâmetros desconhecidos
a amostra constitui um conjunto de n v.a.
X1, X2, ..., Xn independentes e identicamente
distribuídas com distribuição FX

Amostra Aleatória
acetato adaptado de referencia 3
5
Amostra Aleatória
Note que usamos letras minúsculas
pois estamos a definir concretizações
(observações) de variáveis aleatórias
acetato adaptado de referencia 1
Note que usamos letras maiúsculas,
pois estamos a definir variáveis
aleatórias e medidas em função dessas
variáveis
6
Parâmetro vs. Estatística

Parâmetro – Medida usada para descrever a distribuição
da população



a média μ e o desvio padrão σ2 são parâmetros de uma
distribuição Normal - N(μ,σ2)
a probabilidade de sucesso p é um parâmetro da distribuição
Binomial - B(n,p)
Estatística – Função de uma amostra aleatória que não
depende de parâmetros desconhecidos
n i 1

Média amostral:
X1

Variância amostral:
S 1

Amplitude da amostra:
2
n
Xi
n i 1
n
(Xi  X )
2
R  X n:n  X 1:n
7
Parâmetro vs. Estatística
Proporção dos
inquiridos de
raça branca
numa população
e numa amostra
p
exemplo extraído da referência 2
8
Estimação de Parâmetros
População
Amostra
Distribuição da População
Distribuição Amostral
Parâmetros
(valor fixo)
Estimação
estimar
Estatísticas
(função da amostra)
pontual (estatísticas)
por intervalo (intervalos de confiança)
OBS: estatística: é a v.a. que estima (pontualmente) um parâmetro (populacional)
as vezes é chamada simplesmente de estimador
estimativa: é o valor do estimador obtido para uma amostra específica
acetato adaptado de referencia 3
9
Estimação do nº de Votos
Fonte: Projecto ALEA – Noçoes de Estatística
http://alea-estp.ine.pt/Html/nocoes/html/exemplo2_4_1_11.html
10
Construindo a Amostra
Fonte: Projecto ALEA – Noçoes de Estatística
http://alea-estp.ine.pt/Html/nocoes/html/exemplo2_4_1_11.html
11
Conclusões
Resultado: (60,5%, 66,5%) de lisboetas vão votar no presidente com um
grau de confiança de 95%
12
Intervalo de Confiança
Um intervalo de confiança para um parâmetro ,
a um grau de confiança 1-,
é um intervalo aleatório (Linf, Lsup) tal que:
P(Linf <  < Lsup) = 1- ,   (0,1)
onde  deve ser um valor muito reduzido por
forma a temos confianças elevadas
Valores usuais para o grau de confiança: 95%, 99% e 90%
13
Intervalo de Confiança (IC)
I. IC para a média  com variância conhecida

Caso 1: população Normal

Caso 2: população qualquer (n>>30) aproximada pela Normal
II. IC para a média  com variância desconhecida

Caso 1: população Normal

Caso 2: população qualquer (n>>30) aproximada pela Normal
III. IC para a diferença de médias de duas populações Normais

Caso 1: duas amostras independentes, variâncias conhecidas

Caso 2: duas amostras independentes, variâncias desconhecidas

Caso 3: amostras emparelhadas, variâncias desconhecidas
IV. IC para uma proporção
14
IC para  com variância conhecida
Caso 1: População Normal
0,14
X ~ N (  , )
 desconhecido, mas 2 conhecido
2
XX ~~N? (  ,
2
n
)
0,1
centrando e reduzindo:
X 

Z
N (0,1)
0,12
1
0,08

2
0,06
~ ?N (0,1) (Normal Padrão)
0,04
n

2
0,02
0
P(  z  Z  z )  1  
P(  z 
X 

0
-
5
z /2
-z
quantil de ordem /2
 z)  1  
n

P(  z
 X   z
)  1
n
n
10
0
z
15
+
z1 - /2
quantil de ordem 1-/2

P( X  z
Linf

n
 X z

n
Lsup
)  1
IC para  a grau de confiança 1-

 

IC(1 ) (  )   X  z1 2
, X  z1 2

n
n


acetato adaptado de referencia 3
15
Determinando o Quantil de Ordem 1-/2
Distribuição Normal Padronizada
Tabela 3.a. Normal Distribution

2

2
Para nível de significância =0.05
 grau de confiança 95%
(z) = P(Z < z) = 1 - /2  z = z 1 - /2
quantil de ordem 1-/2
(z) = P(Z < z) = 1- (0.05/ 2) = 0.975
buscar valor de z na tabela:
(z) = 0.9750  z = 1.96
Grau de
Confiança
Valor z
90%
1.65
95%
1.96
99%
2.58
90% grau de confiança – existem 10 possibilidades de 100 que o IC não contenha a média populacional
95% grau de confiança – existem 5 possibilidades de 100 que o IC não contenha a média populacional
99% grau de confiança – existe
1 possibilidade de 100 que o IC não contenha a média populacional
16
Interpretação do IC para 
Para uma amostra aleatória de tamanho 50 seguindo uma distribuição
Normal com média  = 10 e variância 2 = 4  X ~ N (10, 4) ,
determinamos o IC para  com 95% de grau confiança:
P( X  1,96
2
2
   X  1,96
)  95%
50
50
P( X  0,5544    X  0,5544)  95%
IC95% (  )  X  0.5544, X  0.5544
=10
Interpretação: 95% dos possíveis ICs
obtidos a partir de uma amostra de
tamanho 50, conterão de facto o
verdadeiro valor da média =10
17
IC para  com variância conhecida
Caso 1: População Normal
Exemplo:
Uma v.a. qualquer tem uma distribuição Normal com média  desconhecida e
variância 2 = 16. Retira-se uma amostra de 25 valores e calcula-se a média
amostral. Construa um IC de 95% para  supondo que X  12,7.
0,14
N (0,1)

 

IC(1 ) (  )   X  z1 2
, X  z10,1

 2
n
n


0,12
0,08


0,06  
IC95% (  )   X  z0.9750
, X  z0.9750

n
n
0,04

0,02
4
4 

 12,7  1,96
,12,7  1.96

0
25
25


0
 12,7 1,568, 12,7  1,568
IC95% ( )  11.132, 14.268
P(11,132    14, 268)  0,95
2,5%
-
5
2,5%
95%
-z
Grau de
Confiança
Valor z
90%
1.65
95%
1.96
99%
2.58
10
0
z
15
+
? =1,96
z0,9750
18
IC & Grau de Confiança
Como poderia obter intervalos de confiança mais estreitos,
ou seja, com limites mais próximos a média verdadeira?
figura extraída da referência 2
Diminuindo o grau de confiança
Diminuindo o grau de confiança de 99% a 95%, aumentamos o risco de estar
errados: de 1% de risco passamos a 5% de risco, ou seja temos mais
possibilidades (5/100 em vez de 1/100) de que o IC não contenha a média
populacional. Ao aumentar o risco, o intervalo deve ser mais preciso
19
IC & Dimensão da Amostra
Como poderia obter intervalos de confiança mais estreitos,
ou seja, com limites mais próximos a média verdadeira?
Aumentando a dimensão da amostra
Tabela extraída da referência 2
20
IC para  com variância conhecida
Caso 2: População Genérica aproximada pela Normal
Se uma distribuição qualquer tiver média  (desconhecida) e
variância 2 (conhecida) e se forem validas as condições do TLC
(n>>30) podemos obter um IC aproximado para a média 
IC para  a grau de confiança 1-
0,14
N (0,1)
0,12
0,1
0,08

 

IC1 (  )   X  z1 2
, X  z1 2

n
n


2
0,06
0,04

2
1
0,02
0
0
-
5
-z
10
0
z
quantil de ordem 1-/2
15
+
20
z1 - /2
21
IC para  com variância conhecida
Resumo
 desconhecido, mas 2 conhecido
IC para  a grau de confiança 1-
IC (  )  X  z1 2
IC (  )  X  z1 2
quanto maior z
 IC menos preciso
X z

n
Se aumentarmos o grau de confiança
 a precisão diminui porque aumenta o valor z
se 90%  z = 1.65
se 95%  z = 1.96
se 99%  z = 2.58

n

n
quanto maior n
 menor o erro padrão
 IC mais preciso
A expressão

é chamada
n
erro padrão (standard error)
22
IC para  com variância desconhecida
Se o valor de 2 é desconhecido  substituir por uma estimativa
Estimadores pontuais para o desvio padrão  :
desvio padrão amostral não-corrigido
1 n
 S
( X i  X )2

n i 1

desvio padrão amostral corrigido
1 n
  Sc 
( X i  X )2

n  1 i 1

Se 2 desconhecida podemos distinguir dois casos:
Caso1. população Normal  usar distr.t de Student
X ~ N ( , 2 )  T 
X 
~ tn 1 
Sc n
S
S 

IC1 (  )   X  t1 2 , n1 c , X  t1 2 , n 1 c 
n
n

Caso2. q.q. distribuição aproximada pela Normal, amostras grandes
 usar distribuição Normal padronizada
Sc
Sc 

X 
IC
(

)

X

z
,
X

z


X q.q. com n  30  Z 
N (0,1) 
1
1 2
1 2
~
n
n

Sc n a
23
IC para  com variância desconhecida
Caso 1: População Normal
Exemplo:
Uma v.a. qualquer tem uma distribuição Normal com média  e variância 2
desconhecidas. Retira-se uma amostra de 25 valores e calcula-se a média amostral e
variância amostral . Construa um IC de 95% para  supondo que X  12,7 e S2 = 16
Distribuição t de Student com
24 graus de liberdade
0,14
S
S 

IC(1 ) (  )   X  t1 2 , n1
, X  t0,12

1 2, n 1
n
n


t24
0,1
S
S 

IC95% (  )   X  t0.9750, 24
, X  t00,08

.9750, 24
n
n

0,06
95%
0,04
4
4 

 12,7  2,064
, 12,7  2,064

0,02
25
25


 12,7 1,6512, 12,7  1,65120
IC95% ( )  11.0488, 14.3512
0
2,5%
-
5
2,5%
-t
10
0
t
15
+
t0,9750,
? 24 = 2,064
P(11,0488    14,3512)  0,95
24
Determinando t1-/2, n-1 - quantil de ordem 1-/2 de
uma distribuição t-Student com n-1 graus de liberdade
Tabela 8. Student s t-Distribution
Por definição de quantil de ordem 1-/2:
z = z 1 - /2  F(z) = P(Z < z) =1 - /2
Para grau de confiança 95%  nível de significância =0.05
F(z) = P(Z < z) = 1- (0.05/ 2) = 0.975  F(z) = 0.9750
Para n=25  24 graus de liberdade
Determinar t0.9750, 24 usando Tabela 8:
t0.9750, 24 = 2.06
25
IC para  com variância desconhecida
Caso 1: População Normal
exercício 5, capítulo 4
Uma amostra aleatória de 20 cigarros foi analisada para estimar a quantidade de
nicotina por cigarro, observando-se a média de 1,2 mg e variância amostral corrigida
de 0.4. Pressupondo que as observações têm distribuição Normal, determine um IC
para o valor médio da quantidade de nicotina por cigarro, grau de confiança de 99%
Usando esta amostra determinamos um IC aproximado para  a 99%:
S
S 

IC(1 ) (  )   X  t1 2,n 1 c , X  t1 2,n 1 c 
n
n

S
S 

IC99% (  )   X  t0,995,19 C , X  t0,995,19 C 
n
n

Para grau de confiança 99%:
(1-) x 100% = 99%  (1-) =0.99  =0.01
Por definição de quantil de ordem 1-/2:
F(z) = P(Z < z) = 1- (0.01/ 2) = 0,995  F(z) = 0.995
Para n=20  19 graus de liberdade
Determinar t0.995, 19 usando Tabela 8
t0.995, 19 = 2.86

0,04
0,04 

IC99% (  )  1,2  2,86
, 1,2  2,86
20
20 

 1,2  2,86  0,044721, 1,2  2,86  0,044721
IC99% ( )  1.0721, 1.3279
26
IC para  com variância desconhecida
Exemplo: População qualquer, amostra grande
Ingressos dos emigrantes hispânicos em EU segundo censo de 1980



Origem
Nº
pessoas
amostra
Rendimento
Médio
Desvio
Padrão
Amostral
IC para  a grau de confiança 95%
cubanos
3895
$16 368
$3 069
mexicanos
5729
$13 342
$9 414
S
S 

IC95% (  )   X  1.96
, X  1.96

n
n

portoriquenhos
5908
$12 587
$8 647
cubanos:
erro padrão 
3069
 49.17
3985
mexicanos: erro padrão 
porto-riq.:
erro padrão 
IC95% ( )  16368  1.96  49.17
IC  ( 16272, 16464 )
9414
 124.41
5729
IC95% ( )  13342  1.96 124.41
8647
 112.5
5908
IC95% ( )  12587  1.96 112.5
IC ( 13098, 13586 )
IC  ( 12367, 12807 )
27
IC para  com variância desconhecida
Exemplo: População qualquer, amostra grande
Exemplo adaptado de referência 2
28
Inferência entre parâmetros
de duas populações
n
m
X
P1
E( X )   X
P2
Y
E (Y )  Y
Mesmo não se conhecendo as médias 1 e 2, seria possível verificar se elas
são iguais a partir de seus valores amostrais?
Se 1 e 2 são iguais, então 1 - 2 = 0.
Podemos a partir da diferença das médias amostrais
da diferença das médias de duas populações
X  Y inferir o valor
acetato adaptado de referencia 3
29
Intervalo de Confiança para 1 - 2
Duas populações Normais. Amostras independentes
Sejam X1,…, Xn e Y1, …, Ym duas amostras aleatórias constituídas por
observações independentes e provenientes de duas populações Normais
N(X, X2) e N(Y, Y2), respectivamente
IC para 12 a grau de confiança 1-
Caso 1: variâncias conhecidas
Caso 2: variâncias desconhecidas mas iguais
30
Intervalo de Confiança para 1 - 2
Populações Normais. Amostras emparelhadas
Sejam X1,…, Xn e Y1, …, Yn duas amostras provenientes de populações Normais
Amostras emparelhadas: se pares de observações (Xi, Yi) são
dependentes sendo todos os restantes pares (Xi, Yj), ij independentes
2
Consideram-se as diferenças: Di  ( X i  Yi ) ~ N (D ,  D )
 D = X- Y – diferença das médias populacionais
 D – desvio padrão das diferenças - desconhecido
mas pode ser estimado através das diferenças D1, …, Dn
 D1, D2, ...Dn – a.a. com população Normal e variância desconhecida
D ~ N (  D ,  2D )  T 
D  D
~ t n 1
S cD n
ScD – desvio padrão amostral
corrigido das diferenças
IC para D= X-Y a grau de confiança 1-

S cD
SCD

IC1 (  D )  D  t1 2 , n 1
, D  t1 2 , n 1

n
n





31
Intervalo de Confiança para Proporção
Considere que uma urna contêm bolas vermelhas e azúis e que n bolas são
escolhidas ao acaso (com reposição), definindo-se
X como o número de bolas vermelhas entre as n seleccionadas
n
X   Yi , Yi ~ Bernoulli sendo p = P(Xi = 1),
X ~ Binomial (n,p)
a probabilidade de se seleccionar um bola vermelha
i 1
Se p- desconhecido, um estimador pontual para p é a proporção amostral:
pˆ 
X
n
pˆ ~ N ( p,
a
Z
pˆ  p

p (1  p ) n
0,14
0,12
centrando e reduzindo:
X
p
n
p (1  p ) n
p(1  p)
) (se n é grande, pelo TLC)
N (0,1)
n
0,1
1
0,08

2
0,06
~ N (0, 1)
0,04
0,02
a
0
0
I.C. para Z com grau de confiança 1-
P(  z  Z  z )  1  

2
-
5
z /2
-z
quantil de ordem /2
10
0
z
15
+
z1 - /2
20
quantil de ordem 1-/2
P( pˆ  z pˆ (1  pˆ ) n , pˆ  z pˆ (1  pˆ ) n )  1  
32
Intervalo de Confiança para Proporção
X
Seja pˆ 
a proporção de indivíduos com uma certa característica de
n
interesse numa amostra aleatória de dimensão n, e p a proporção de
indivíduos com essa característica na população.
Um intervalo de confiança aproximado para p, a um grau de confiança
1-, é dado por:

IC(1 ) ( p )   pˆ  z1 2

pˆ (1  pˆ )
, pˆ  z1 2
n
pˆ (1  pˆ ) 


n

33
IC para uma proporção
Exemplo: Proporção de acessos a páginas de Internet nacionais
exercício 16, capítulo 4
Em 100 acessos a páginas de internet escolhidos ao acaso 30 são as páginas
nacionais. Determine um IC a 95% para a proporção de acessos a páginas nacionais
X - número de acessos á páginas de internet nacionais
X ~ Binomial( 100,p)
p – proporção de acessos a páginas nacionais (em geral)
p – desconhecido
Usando esta amostra determinamos um IC aproximado para p a 95%:
pˆ (1  pˆ )
IC(1 ) ( p)  pˆ  z1 2 S p , pˆ  z1 2 S p com pˆ  X
e Sp 
n
n
1º. Determinar z1-/2 para =0,05
z0,9750=1,96


IC(95%) ( p)   pˆ  z0.9750S p , pˆ  z0.9750S p 
IC(95%) ( p)   pˆ  1,96  S p , pˆ  1,96  S p 
2º. Determinar as estimativas ^
p e Sp
pˆ 
X
30

 0.3
n 100
Sp 
pˆ (1  pˆ )
0,3  0,7

 0,04582
n
100
3º. Substituir na fórmula:
IC(95%) ( p)  0,3  1,96  0,04582, 0,3  1,96  0,04582
 0,3  0,089818, 0,3  0,089818
IC95% ( p)  0.2102, 0.3898
34
Formulário
F
O
R
M
U
L
Á
R
I
O
extraído do formulário da disciplina Métodos Numéricos e Estatísticos disponível no blackboard
(buscar em lista disciplinas do curso: 8264 - Lic. Biotecnologia (1º ciclo))
35
Referências
Livro: Grande Maratona de Estatística no SPSS
Andreia Hall, Cláudia Neves e António Pereira
Capítulo 4.1 Intervalos de Confiança
Acetatos disponíveis on-line usados na elaboração destes acetatos:

Estatística Inferencial e Intervalos de Confiança, Amostragem
Andreia Hall
URL: http://www2.mat.ua.pt/pessoais/AHall/me/files/acetatos.htm
http://www2.mat.ua.pt/pessoais/AHall/Bioestat%EDstica/Bioestat%EDstica.htm

Chapter 11: Sampling and Sampling Distribution, Chapter 12: Estimation
Prof. J. Schwab , University of Texas at Austin
disciplina: Data Analysis I (spring 2004)
URL: www.utexas.edu/courses/schwab/sw318_spring_2004/TextbookLectureNotes

Estimação
Camilo Daleles Rennó, Instituto Nacional de Pesquisas Espaciais, Brasil
disciplina:Estatística: Aplicação ao Sensoriamento Remoto (2008)
URL: http://www.dpi.inpe.br/~camilo/estatistica/notas.html

Estimação por Intervalos
Ana Pires, IST Lisboa
disciplina: Probabilidades e Estatística
URL: : http://www.math.ist.utl.pt/~apires/materialpe.html
36