Sistema Trifásico - Site do Getúlio Teruo Tateoki

Sistema Trifásico
Prof. Ms. Getúlio Teruo Tateoki
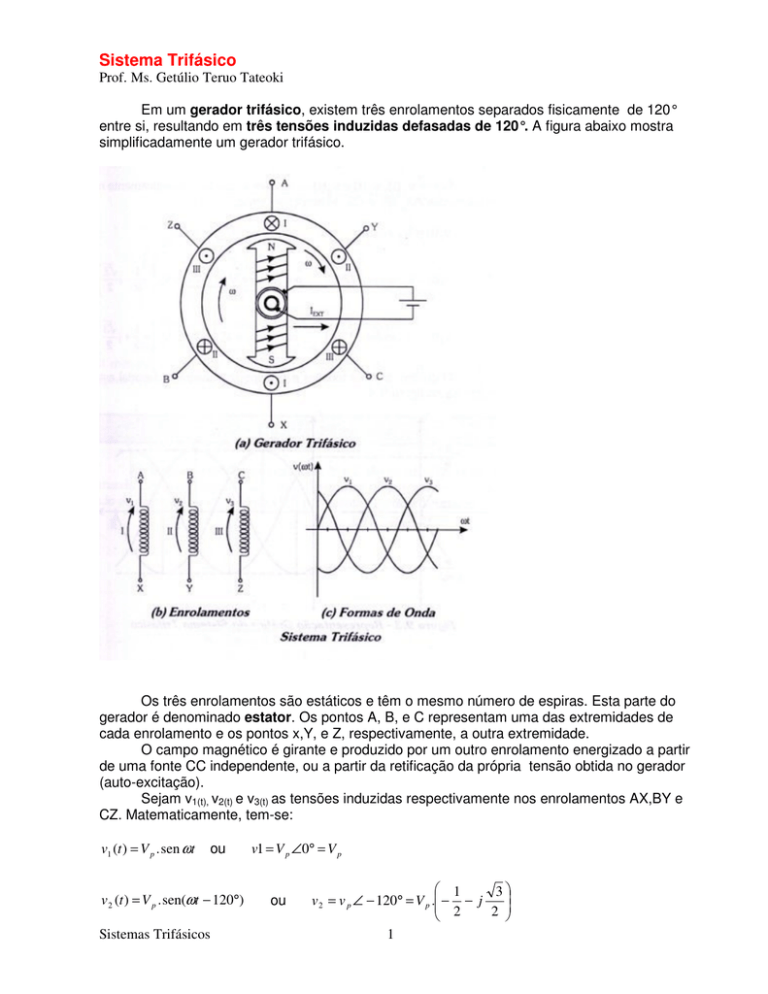
Em um gerador trifásico, existem três enrolamentos separados fisicamente de 120°
entre si, resultando em três tensões induzidas defasadas de 120°. A figura abaixo mostra
simplificadamente um gerador trifásico.
Os três enrolamentos são estáticos e têm o mesmo número de espiras. Esta parte do
gerador é denominado estator. Os pontos A, B, e C representam uma das extremidades de
cada enrolamento e os pontos x,Y, e Z, respectivamente, a outra extremidade.
O campo magnético é girante e produzido por um outro enrolamento energizado a partir
de uma fonte CC independente, ou a partir da retificação da própria tensão obtida no gerador
(auto-excitação).
Sejam v1(t), v2(t) e v3(t) as tensões induzidas respectivamente nos enrolamentos AX,BY e
CZ. Matematicamente, tem-se:
v1 (t ) = V p . sen ωt
ou
v 2 (t ) = V p . sen(ωt − 120°)
Sistemas Trifásicos
v1 = V p ∠0° = V p
ou
v 2 = v p ∠ − 120° = V p . −
1
1
3
− j
2
2
v 3 (t ) = V p . sen(ωt + 120°)
ou
v 3 = V p ∠120° = V p . −
1
3
+ j
2
2
O gráfico das três tensões e o respectivo diagrama fasorial estão mostrados abaixo:
Se cada fase do gerador é conectada a circuitos separados, o sistema trifásico é
chamado de não interligado, necessitando de seis fios para a conexão de carga trifásica,
como mostra a figura abaixo:
Este método não é econômico, não sendo usado na prática. Existem dois métodos
comuns de interligar as fases em um sistema trifásico: as ligações estrela (Y) e triângulo ou
delta ( ).
Sistemas Trifásicos
2
Ligação Estrela
Na ligação estrela, os pontos X,Y, e Z são interligados entre si, formando um ponto
comum chamado de neutro(N), sendo este ponto ligado ao neutro da carga. A figura abaixo
representa este tipo de ligação.
A corrente no fio neutro é a soma vetorial das correntes de fase, isto é:
iN = iA + iB + iC
Tensões de Fase e de Linha
As tensões medidas entre os terminais do gerador (pontos AB,BC e CA) são chamadas
de tensões de linha (vAB,vBC e vCA) ou, genericamente, vL.
Na figura anterior, as setas das tensões dão a orientação positiva (arbitrária), podendose equaciona-las do seguinte modo:
VAB = vA – vB
vBC = vB – vC
vCA = vC - vA
Estes três expressões significam que, em cada instante, as tensões de linha (vAB,vBC e
vCA) são iguais às diferenças entre os valores instantâneos das respectivas tensões de fase
(vA,vB,vC).
As tensões de fase podem ser escritas como:
v A (t ) = V p . sen ωt
v A = V F ∠0° = V F
ou
v B (t ) = V P . sen(ωt − 120°)
ou
v B = V F ∠ − 120° = V F . −
v C (t ) = V P . sen(ωt + 120°)
ou
v C = V F ∠120° = V F . −
As tensões de linha podem ser escritas como:
Sistemas Trifásicos
3
1
3
− j
2
2
1
3
+ j
2
2
v AB = v A − v B = V F − V F . −
Portanto:
3
1
+ j
2
2
v AB = 3.V F ∠30°
v BC = v B − v C = V F . −
Portanto:
1
3
3
3
− j
= VF . + j
= 3.V F
2
2
2
2
(
)
1
3
1
3
− j
− VF . − + j
= V F − j 3 = − j 3.V F
2
2
2
2
v BC = 3.V F ∠ − 90°
v CA = v C − v A = V F . −
1
3
3
3
3
1
− j
− VF = VF . − + j
= − 3.V F . −
+ j
2
2
2
2
2
2
Portanto:
v CA = 3.V F ∠150°
Assim, conclui-se que a relação entre os módulos das tensões de linha vL e de fase vF é
dada:
V L = 3.V F
Observação:
•
Cuidado pois as tensões de linha e de fase são normalmente dadas em valores
eficazes.
Exemplo:
A tensão de linha num sistema trifásico cuja tensão de fase é de 220VRMS vale:
V L = 3.V F = 3.220 ≅ 381Vrms
A figura abaixo mostra o diagrama fasorial das tensões de fase e de linha num sistema
trifásico em ligação estrela.
Sistemas Trifásicos
4
Cargas Balanceada e Desbalanceada
fase.
Num sistema trifásico, a carga é balanceada quando Z1,Z2 e Z3 são iguais em módulo e
Neste caso, as defasagens entre tensão e corrente em cada fase são iguais, isto é,
, como mostra a figura abaixo:
A =
B =
C =
Sistemas Trifásicos
5
Porém, a carga é desbalanceada quando Z1, Z2, e Z3 possuem módulos ou fases
diferentes, caso em que as defasagens entre tensão e corrente em cada fase são também
diferentes, isto é: φ A ≠ φ B ≠ φ C
Correntes de Fase e de Linha
A corrente que percorre cada fase é chamada de corrente de fase, designada
genericamente por iF. A corrente que passa na linha que liga o gerador à carga é chamada de
corrente de linha, designada genericamente por iL. No caso de Ligação estrela, iL = IF.
Se a carga é balanceada, a corrente no fio neutro é zero, isto é iN = 0. Se a carga é
desbalanceada, a corrente no fio neutro é diferente de zero, isto é iN 0 ou, caso não haja o
fio de retorno (neutro), as tensões nas cargas são diferentes.
Exemplos:
Dado o circuito a seguir, pede-se:
Sistemas Trifásicos
6
a) Tensões de fase e de linha
VF = 120V
V L = 3.V F = 3.120 = 208V
b) Correntes de fase, de linha e no fio neutro
120
= 12 A
10
Como a carga é resistiva, as correntes de linha há estão em fase com suas tensões, porém
defasadas de 120° entre si, isto é:
IF = IL =
i A = 12∠0° = 12 A
i B = 12∠ − 120° = −6 − j10,39 A
Portanto:
i N = i A + i B + iC = 12 + ( −6 − j10,39) + ( −6 + j10,39) = 0 A
2) Dados o circuito a seguir, pede-se a corrente no fio neutro:
Sistemas Trifásicos
7
iC = 12∠120° = −6 + j10,39 A
iA =
120∠0°
= 12∠0° = 12 A
10
iC =
120∠120°
= 6∠120° = −3 + j 5,2 A
20
iB =
120∠ − 120°
= 10∠ − 120° = −5 − j8,66 A
12
Portanto:
i N = i A + i B + iC = 12 + ( −5 − j8,66) + (−3 + j 5,2) = 4 − j 3,46 = 5,29∠ − 40,9° A
Ligação Triângulo
Na ligação triângulo ou delta, as extremidades dos enrolamentos do gerador são
interligadas de modo a formar um triângulo, como mostra a figura abaixo:
Tensões e Correntes de Fase e de linha
Nesta ligação, vAB, vBC e vCA correspondem às tensões de fase vF e de linha vL, ou seja:
V F = vL
Já, as correntes de fase nas cargas iF(iAB,iBC,iCA) são diferentes das correntes de linha
iL(iA,iB,iC), que podem ser calculadas por:
IA = iAB – iCA
iB = iBC – iAB
iC = iCA - iBC
No caso de carga balanceada, as defasagens entre tensão e corrente em cada fase
são iguais, isto é, A = B = C = , como mostra a figura abaixo:
Sistemas Trifásicos
8
Porém, quando a carga é desbalanceada, as defasagens entre tensão e corrente em
cada fase são diferentes, isto é, φ A ≠ φ B ≠ φ C
As tensões de linha ou de fase podem ser escritas como:
v AB = (t ) = V p . sen ωt
v AB = V L ∠0° = V L
ou
v BC (t ) = V P . sen(ωt − 120°)
ou
v BC = V L ∠ − 120° = V L . −
v CA (t ) = V P . sen(ωt + 120°)
ou
v CA = V L ∠120° = V L . −
1
3
− j
2
2
1
3
+ j
2
2
A relação entre os módulos de linha iL, e de fase iF pode ser determinada da mesma
maneira feita com tensões de linha e de fase na ligação estrela, obtendo se:
i L = 3.i F
Exemplo:
Dado o circuito a seguir, pedem-se:
Sistemas Trifásicos
9
a) Corrente de fase em cada carga
v AB 380∠0°
=
= 19∠0° = 19 A
Z1
20
v
380∠ − 120°
= BC =
= 19∠ − 120° = −9,5 − j16,45 A
Z3
20
i AB =
i BC
i CA =
v CA 380∠120°
=
= 19∠120° = −9,5 + j16,45 A
Z3
20
b) Correntes de linha
i A = i AB − i CA = 19 − (−9,5 + j16,45) = 28,5 − j16,45 = 32,9∠ − 30° A
i B = i BC − i AB = (−9,5 − j16,45) − 19 = −28,5 − j16,45 = 32,9∠ − 150° A
iC = i CA − i BC = (−9,5 + j16,45) − (−9,5 − j16,45) = j 32,9 = 32,9∠90° A
Potência em Sistemas Trifásicos
Em um sistema monofásico, a potência ativa (real) é dada por:
P=VF.IF.cosø [W], onde VF e IF são respectivamente, a tensão e a corrente de fase eficazes e ø
o ângulo de defasagem entre eles.
Em um sistema trifásico balanceado, as potências ativas em cada fase são iguais, de
forma que a potência ativa total é a soma das potências ativas nas fases, isto é:
P=3VF.IF.cosø [W]
(VF e IF em valores eficazes)
V
Na ligação estrela, tem-se que IF=IL e V F = L
expressão da potência ativa, resulta:
Sistemas Trifásicos
10
3
Substituindo estes valores na
P = 3.
VL
3
P = 3.V L .I L . cos φ [W]
.I L . cos φ
Na ligação triângulo, tem-se que VF = VL e I F = I L
expressão da potência ativa, resulta:
P = 3.
IL
3
3
. Substituindo estes valores na
P = 3.V L .I L . cos φ [W]
.V L . cos φ
Disto, conclui-se que a expressão para a potência ativa total é a mesma para as
ligações estrela e triângulo, mas as potências são diferentes.
Usando o mesmo raciocínio, podem-se determinar as potências reativa e aparente totais
no sistema trifásico para ambas as ligações, considerando-se os sistemas balanceados.
A potência reativa total na carga trifásica é:
PR=3.VF.IF.senø [VAR]
PR = 3.V L .I L . sen φ [VAR]
ou
A potência aparente total na carga trifásica é:
PAP=3.VF.IF [VA]
ou
PAP = 3.V L .I L [VA]
Caso os sistemas trifásicos não sejam balanceados, as potências totais correspondem às
somas das potências dissipadas pelas cargas.
Exemplos:
1) dado o circuito a seguir, pedem-se:
Sistemas Trifásicos
11
a) Tensões de fase e de linha:
VF = 220VRMS
V L = 3.V F = 3.220 = 381V RMS
b) Correntes de fase, de linha e no fio neutro
IL = IF =
V F 220
=
= 22 ARMS
R
10
Como a carga é balanceada, IN = 0 A.
c) Potência ativa dissipada na carga trifásica:
P = 3.VF.IF.cosø = 3.220.22.1 = 14,52kW
ou
P = 3.V L .I L . cos φ = 3.381.22.1 = 14,518kW
Os resultados devem ser iguais. Esta diferença se deve aos arredondamentos.
2) A potência de um motor trifásico é 8kW quando ligado a uma tensão de linha de
380VRMS. Calcular a corrente de linha se o fator de potência é 0,85.
P = 3.V L .I L . cos φ
8.10 3 = 3.380.I L .0,85
I L = 14,3 ARMS
3) Um aquecedor trifásico é constituído de três resistências de 20 ligadas em estrela.
Calcular a corrente de linha e a potência ativa total se a tensão de linha é 220VRMS.
VF =
VL
3
=
220
3
Sistemas Trifásicos
= 127V RMS assim: I L = I F =
V F 127
=
= 6,35 ARMS
R
20
12
Portanto:
P = 3.V L .I L . cos φ
8.10 3 = 3.220.6,35.1 = 2,42kW
4) Os enrolamentos de um motor têm resistência de 6 e reatância indutiva de 8 .
Sabendo-se que o motor é ligado em estrela e que a tensão de linha é 220VRMS, calcular:
a) Correntes de linha e de fase:
Tem-se: z=6+j8
assim:
| Z |= 6 2 + 8 2 = 10Ω
A tensão de fase vale:
VF =
VL
3
=
220
3
= 127V RMS
portanto: I F = I L =
V F 127
=
= 12,7 ARMS
R
10
b) Potências ativa e aparente:
cos φ =
R 6
=
= 0,6
Z 10
P = 3.V L .I L . cos φ = 3.220.12,7.0,6 = 2,9kW
PAP = 3.V L .I L 3.220.12,7 = 4,84kVA
5) Idem ao exercício anterior, porém considerando o motor ligado em triângulo.
Sistemas Trifásicos
13
c) Correntes de linha e de fase:
VF = VL = 220VRMS
IF =
V F 220
=
= 22 ARMS
Z
10
I L = 3.I F = 3.22 = 38,1ARMS
d) Potências ativa e aparente:
P = 3.V L .I L . cos φ = 3.220.38,1.0,6 = 8,71kW
PAP = 3.V L .I L = 3.220.38,1 = 14,52kVA
Conclusão importante:
Na carga triângulo, a corrente de linha é três vezes maior que na carga estrela,
quando ligadas na mesma tensão. Como conseqüência, a potência também é três vezes
maior.
6) O circuito a seguir, mostra o secundário de um transformador ligado em triângulo, com uma
tensão de linha de 127VRMS. A carga é constituída de um motor trifásico de 5kW com FP =
0,85, e de três motores monofásicos de 2kW e FP=0,8, cada um ligado a uma fase.
Determinar:
Sistemas Trifásicos
14
a) Potências ativa, aparente e reativa da instalação:
Motor trifásico:
P = 5kW
PAP =
P
5000
=
= 5,88kVA
cos φ 0,85
cos φ = 0,85
φ = 31,8°
PR = PAP.senø = 5882.sen31,8° = 3,099kVAR
Motores monofásicos:
P = 2kW (de cada motor)
PAP =
P
2000
=
= 2 ,5 kVA
cos φ
0,80
Como os motores são iguais, a potência aparente dos três motores monofásicos é:
cos φ = 0,8
PAP = 3.2500 = 7,5kVA
φ = 36,9°
A potência reativa dos três motores é:
PR = PAP.senø = 5882.sen36,9° = 7500.0,6 = 4,5kVAR
A potência ativa total é:
PT = 5000 + 3.2000 = 11kW
A potência reativa total é:
PRT = 3099 + 4500 = 7,599kVAR
A potência aparente total é:
PApT = PT2 + PRT2 = 112 + 7,599 2 = 13,37 kVA
b) Corrente total de linha:
PApT = 3.V L .I L
IL =
13370
3.127
= 60,78 ARMS
c) Fator de potência da instalação:
PT = PApT . cos φ T
cos φ T =
PT
11
=
= 0,823
PApT 13,37
Bibliografia: Circuitos em Corrente Alternada – Rômulo Oliveira Albuquerque, Editora Érica,
6ª Edição
Sistemas Trifásicos
15