simulado - extensivo – ita/medicina

3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
01. Exercício 13, aposila 01 (MAT - C) - pag. 07
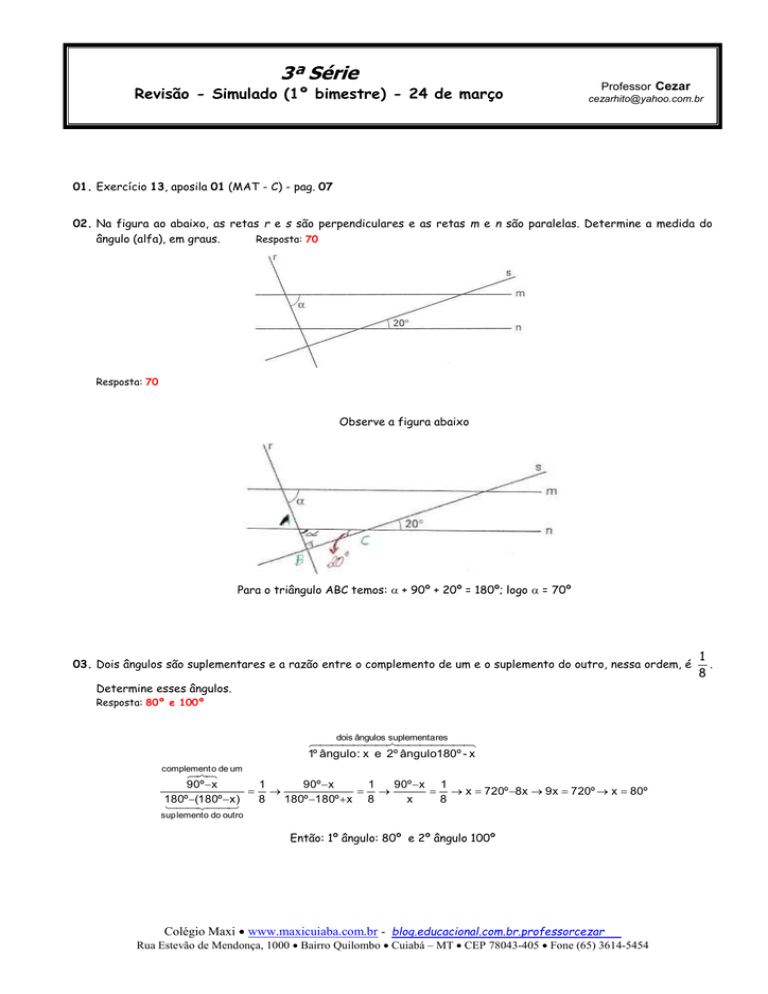
02. Na figura ao abaixo, as retas r e s são perpendiculares e as retas m e n são paralelas. Determine a medida do
ângulo (alfa), em graus.
Resposta: 70
Resposta: 70
Observe a figura abaixo
Para o triângulo ABC temos:  + 90º + 20º = 180º; logo  = 70º
03. Dois ângulos são suplementares e a razão entre o complemento de um e o suplemento do outro, nessa ordem, é
Determine esses ângulos.
Resposta: 80º e 100º
dois ângulos suplementares


1º ângulo : x e 2º ângulo180º - x
complement o de um

90º  x
1
90º  x
1
90º  x 1
 
 
  x  720º 8 x  9 x  720º  x  80º
180
(
180

x)
8
180º 180º  x 8
x
8
º
º
sup lemento do outro
Então: 1º ângulo: 80º e 2º ângulo 100º
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
1
.
8
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
04. A razão entre dois ângulos suplementares é de 2 para 7. Determine o complemento do menor.
Resposta: 50º
dois ângulos suplementares


1º ângulo : x e 2º ângulo180º - x
x
2
  7 x  360º 2x  9 x  360º  x  40º
180º  x 7
então : 1º ângulo : 40º
 e 2º ângulo : 140º

menor
maior
Complemento do menor : 90º40º  50º
05. As retas r1 e r2 são paralelas. O valor do ângulo , apresentado na figura a seguir, é:
Resposta: 40º
Observe a figura abaixo a reta “t” que passa pelo ângulo reto, considerando t//r//s
 + 50º = 90º   = 40º
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Professor Cezar
Revisão - Simulado (1º bimestre) - 24 de março
[email protected]
06. Na figura abaixo, as retas r e s são paralelas. Calcule .
Resposta: 20º (Atenção: Gabarito correto: 52º)
Observe a figura abaixo a reta “t” que passa pelo ângulo do vértice B, considerando t//r//s
(180º - 3) + (180º - 2) = 100º  180º - 3 + 180º - 2 + 180º = 100º  -5 = - 260º   = 52º
07. Um aluno começou a prova simulado de matemática às 07 horas 37 minutos e terminou às 09 horas 23 minutos.
Qual o tempo de duração de realização de prova deste determinado aluno.
Resposta: 1 hora 46 minutos
hora
 60
-1

 

minutos


09 horas 23 minutos
08 horas 83 minutos

07 horas 37 minutos

07 horas 37 minutos

1 hora 46 minutos
08. Um determinado motorista inicia sua viagem em Cuiabá às 11 horas e 49 minutos e chega em Rondonópolis às 14
horas e 27 minutos. Qual o tempo de duração da viagem em horas e minutos?
Resposta: 2 horas 12 minutos (Atenção: Gabarito correto: 2 horas 49 minutos)
hora
 60
-1


 

minutos


14 horas 27 minutos 
11 horas 49 minutos
13 horas 87 minutos

11 horas 49 minutos

2 horas 38 minutos
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Professor Cezar
Revisão - Simulado (1º bimestre) - 24 de março
[email protected]
09. Dois dos lados de um triângulo isósceles medem 10 cm e 4 cm. Então é correto afirmar que:
a) seu perímetro pode ser 18 cm
b) seu perímetro pode ser 20 cm
c) seu perímetro é 24 cm
d) seu outro lado pode medir 5 cm
e) seu outro lado pode medir 8 cm
Resposta: c
Considerando um triângulo de lados “a”, “b” e “c”, para existência do triângulo é necessário que:
a + b > c, a + c > b e b + c > a, portanto:
Não é possível construir um triângulo isósceles com lados 4 cm, 4 cm e 10 cm, devido a 4 + 4 < 10
O triângulo isósceles possível é com lados 10 cm, 10 cm e 4 cm, logo o
perímetro P (soma dos lados) do triângulo é: P = 10 + 10 + 4 = 24 cm
10. Dois lados, AB e BC, de um triângulo ABC medem respectivamente 8 cm e 21 cm. Quanto poderá medir o terceiro
lado, sabendo que é múltiplo de 6?
Resposta: 18 cm ou 24 cm
Sabendo que o triângulo é ABC e AB = 8 cm, BC = 21 cm e AC = x(terceiro lado), temos:
8  21  x  x  29

8  x  21  x  13 portanto 13  x  29, logo
21  x  8  x  13

x

18

e
múltiplo de 6
x

24

múltiplo de 6
11. Se dois lados de um triângulo isósceles medem 38 cm e 14 cm, qual poderá ser a medida do terceiro lado?
Resposta: 38 cm
Considerando um triângulo de lados 38 cm, 14 cm e “x”, para existência do triângulo é necessário que:
a + b > c, a + c > b e b + c > a, portanto:
Não é possível construir um triângulo isósceles com lados 14 cm, 14 cm e 38 cm, devido a 14 + 14 < 38
O triângulo isósceles possível é com lados 38 cm, 38 cm e 14 cm,
logo o terceiro lado deve ter a medida igual a 38 cm
12. O lado AB de um triângulo ABC é expresso por um número inteiro. Determine o seu valor máximo, sabendo que os
lados AC e BC, respectivamente 27 cm e 16 cm e ângulo C < ângulo A < ângulo B
Resposta: 15 cm
Sabendo que o triângulo é ABC e AB = x, AC = 27 cm e AC = 16, temos:
Sabendo queângulo C  ângulo A  ângulo B, então AB  AC  BC



O menor ângulo é oposto ao menor lado
x  27  16  x  11
sabendo que AB  x é o menor lado

x  15 cm
x  16  27  x  11 , portanto 11  x  53,
sabendo que AC  27cm e BC  16 cm
27  16  x  x  53

Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
13. Um polígono regular possui a partir de um de seus vértices tantas diagonais quantas são as diagonais de um
hexágono. Ache:
a) o polígono
b) o total de diagonais
c) a soma dos ângulos internos
d) a soma dos ângulos externos
e) a medida de cada ângulo interno
f) a medida de cada ângulo externo
Resposta: a) dodecágono; b) 54; c) 1800º; d) 360º
e) 150º f) 30º
a)
d6


diagonais do hexágono
Sabendo que de cada vértice de cada polígono partem
6(6  3)

 d6  9 
2

tantas diagonais quantos o número de vértices menos três vértices
temos n  d6  3  n  9  3  n  12 (dodecágon o)
b)
d12


diagonais do dodecágono
c)
Si

Soma dos ângulos internos dodecágono
12(12  3)
 d6  54
2
 Si  180 º (12  2)  Si  1800 º
d)
Se

Soma dos ângulos externos dodecágono
e)
ai

 ai 
Si
1800 º
 ai 
 ai  150 º
n
12
 ae 
Se
360 º
 ae 
 ae  300 º
n
12
ângulos interno dodecágono
f)
ae

 Se  360 º
ângulos externo dodecágono
14. Determine o número de diagonais de um polígono regular convexo cujo ângulo externo vale 24º.
Resposta: 90
ae 
Se
360 º
360 º
 24º 
n 
 n  15
n
n
24º
d
n(n  3)
15(15  3)
d
 d  90
2
2
15. Um polígono regular tem 170 diagonais. Quantas passam pelo centro?
Resposta: 10
d
n1  20
n(n  3)
n(n  3)

 170 
 170  2  n2  3n  n2  3n  340  0 n2  17

2
2
 
não convém
ddiagonais que passam pelo centro 
d
2
para definirmos quantas diagonais passam pelo centro
o polígono deve ser regular e ter número par de lados
ddiagonais que passam pelo centro 
20
 ddiagonais que passam pelo centro  10
2
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
16. O ângulo interno de um polígono regular mede 140º. Quantas diagonais passam pelo centro?
Resposta: nenhuma
ai 
S1
180 º (n  2)
 140 
 140  n  180 º n  360 º  40n  360  n  9
n
n
ddiagonais que passam pelo centro 
d
2
para definirmos quantas diagonais passam pelo centro
o polígono deve ser regular e ter número par de lados
ddiagonais que passam pelo centro  nenhuma
17. A razão entre o ângulo interno e o ângulo externo de um polígono regular é 9. Determine o número de lados do
polígono.
Resposta: 20
Si
ai
180º (n - 2)
 9  n  9 
 9  n  2  18  n  20
S
ae
360º
e
n
18. Exercício 49, aposila 01 (MAT - C) - pag. 19
19. Exercício 52, aposila 01 (MAT - C) - pag. 19
20. Os vértices de um hexágono regular estão localizados nos pontos médios das arestas de um cubo conforme a
figura a seguir.
Se uma formiga caminha sobre os lados do hexágono, qual deve ser o ângulo que ela realiza ao passar de um lado
para o lado subsequente
Resposta: 60º
Para passar de um lado para o lado subsequent e a formiga deve realizar um ângulo equivalent e
ao ângulo externo do polígono
então : ae 
Se
360 º
 ae 
 ae  60 º
n
6
21. Exercício 60, aposila 01 (MAT - C) - pag. 23
22. Exercício 64, aposila 01 (MAT - C) - pag. 23
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
23. Observe a figura.
Nessa figura, AB é um diâmetro do círculo de centro O e raio 5, sabendo que AP vale 8, determine PB
Resposta: 6
Observe a figura abaixo
Arco AB  180º

Sabendo que o triângulo APB é retângulo 
Arco AB
 90º
ângulo inscrito AP̂ B 
2

(AB)2 = (AP)2 + (PB)2  102 = (PB)2 + 82  PB = 6
24. Um ângulo inscrito é formado por uma corda e um diâmetro. O arco subentendido pela corda é o dobro do arco
compreendido entre os lados. Determine o ângulo central demarcado na circunferência pelo ângulo inscrito .
Resposta: 30º (Atenção: Gabarito correto: 60º)
Observe a figura abaixo
arco PB  x
Consideran do 
temos 2x  x  180º , então x  60º
arco AP  2x
Ângulo central = x = 60º
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
25. Seja o pentágono PQRST da figura, inscrito na circunferência de centro 0. Sabe-se que POQ mede 70°. Chamando
de x e y os ângulos PTS e QRS, respectivamente, determine x + y.
Resposta: 215º
Observe a figura abaixo
arco PQRS  2  ângulo PT̂S  2x

Sabendo que 

arco QPTS  2  ângulo PQ̂R  2y
o arco PQ foi "usado" duas vezes



2x  2y  360 º 70 º
 2(x  y)  430 º  x  y  215 º
26. Considerando o exercício 35 determine o ângulo PSQ
Resposta: 35º
PŜQ é um ângulo inscrito que demarca na circunferência o arco PQ  70º
Por tan to PŜQ 
arco PQ 70º

 35º
2
2
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
27. Nessa figura, AB é um diâmetro do círculo de centro O e raio 2 e o ângulo PBA mede 60°.
Nesse caso, determine o polígono regular cujo segmento PB representa um dos lados.
Resposta: dodecágono (Atenção: Gabarito correto: hexágono)
Observe a figura abaixo
Arco AB  180º

Arco AB

Sabendo que o triângulo APB é retângulo ângulo inscrito AP̂ B 
 90º
2


ângulo PB A  60º e ângulo BP̂ A  30º

PÂB é um ângulo inscrito que demarca na circunferência o arco PB
por tan to PÂB 
arco PB
arco PB
 30 º 
 arco PB  60 º
2
2
consideran do n o número de lados do polígono, temos n 
360º
 n  6 (hexágono)
60º
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454
3ª Série
Revisão - Simulado (1º bimestre) - 24 de março
Professor Cezar
[email protected]
28. Na figura, A, B, C e D são pontos de uma circunferência, a corda CD é bissetriz do ângulo ACB e as cordas AB e
AC têm o mesmo comprimento. Se o ângulo BÂD mede 40°, determine o valor do ângulo 
Resposta: 20º
Observe a figura abaixo
Sabendo que as cordas AB e AC têm o mesmo comprimento o triângulo ABC é isósceles,
portanto : ângulo AB̂C  ângulo AĈB  2x
BÂD é um ângulo inscrito que demarca na circunferência o arco BD
por tan to BÂD 
arco BD
arco BD
 40 º 
 arco BD  80 º
2
2
BĈ D  x , é um ângulo inscrito que demarca na circunferência o arco PB
por tan to ângulo BĈD  x 
arco BD
80º
x
 x  40º
2
2
Para o triângulo ABC, temos:  + 2x + 2x = 180º   + 4x = 180º   + 4 40º = 180º   = 20º
30. Exercício Resolvido III, aposila 01 (MAT - C) - pag. 22
Colégio Maxi  www.maxicuiaba.com.br - blog.educacional.com.br.professorcezar
Rua Estevão de Mendonça, 1000  Bairro Quilombo  Cuiabá – MT  CEP 78043-405  Fone (65) 3614-5454