Resolução 2ª Frequência 01-2002

Instituto Superior de Ciências do Trabalho e da Empresa
FUNDAMENTOS
DE
ELECTRÓNICA
ETIB1/ETIB2
Resolução da 2ª Frequência 01/02
I. Semicondutores
1.
a) Arbitrando o referencial definido pelos versores são u x , u y
e u z , o potencial
eléctrico V(x, y, z) é dado pela seguinte equação:
V(x, y, z) 
y
  2
a

v
v
v
E    v    ux 
 uy 
 uz
x
y
z

E

2
 u y  200 u y Vm 1
0.01

Felectrão   q  E  321.8 u y N 

,

E  200 Vm 1


Flacuna  q  E  321.8 u y N 
O campo vectorial E e as forças electricas são ambos constantes ao longo do
semicondutor, tal como estão representados na figura.
Os movimentos de um electrão livre e de uma lacuna no semicondutor são obviamente
em sentidos opostos.
b) Os átomos de boro injectados na estrutura cristalina do semicondutor intrínseco vão
adaptar-se a esta como se fossem átomos de silício. No entanto, como os átomos de
boro têm três electrões de valência, são asseguradas apenas três ligações covalentes
aos átomos de silício vizinhos ficando a quarta ligação incompleta, dado que recebe um
electrão do átomo de silício e nenhum do átomo de boro. Esta carência de um electrão
numa orbital, de modo a formar correctamente as quatro ligações com os seus átomos
vizinhos é vulgarmente designada como lacuna. Tal como se representa na figura, esta
vaga numa das ligações torna a carga localmente neutra, pelo que, em média, e desde
que não seja aplicado nenhum campo eléctrico ao dispositivo, cada lacuna fica junto a
um átomo de boro. Quando é aplicado um campo eléctrico à estrutura, é natural que um
electrão de uma ligação covalente vizinha acabe por ser atraído e capturado pela
lacuna, ficando as ligações em torno do átomo de boro totalmente preenchidas, mas
dando origem a uma nova lacuna na orbital de onde saiu o electrão do átomo de silício
vizinho. Assim, podemos considerar que houve uma movimentação desse electrão num
sentido, ou uma movimentação da lacuna no sentido oposto (que na prática significam a
mesma coisa). Em média, sob o efeito de um campo eléctrico, as lacunas movimentam-se
no mesmo sentido desse campo assegurando assim que há transporte de carga e
consequentemente corrente eléctrica. Tal como acontece com os electrões livres,
também as lacunas se movem facilmente sob o efeito da agitação térmica. Um átomo
de boro que perca a sua lacuna, i.e. que receba um electrão, passa a ser um ião negativo.
A figura representa a estrutura atómica na vizinhança de um átomo aceitador.
Naturalmente, a carga móvel disponível nesta estrutura será maioritariamente do tipo
p (i.e. lacunas).
c) A condutividade num semicondutor dopado depende essencialmente da concentração de
impurezas, sendo dada pela seguinte fórmula:
  n   n  p   p  q ,
então,
como
p >> n ,
 p  480 cm2V 1s 1 
e
q  1.609  10-19 C 
  p   p  q  1016  480 1.609  10-19  0.772 S  cm 1   77.232 S  m1 
O valor da resistência eléctrica deste semicondutor e a corrente que o percorre são
dados pelas seguintes equações:
R 
I
V
R
l
A


I
R
c
1
0.01
  64.74 


 l  a 77.232 0.002  0.001
1

10
A  0.1545 A  154.5 mA
64.74
O valor da densidade de corrente eléctrica é dado por:

J  77.232  1000 u x A  m 2

J  E

J  77.232 u x mA  mm2


J  77.232  103 u x A  m 2



O vector J tem naturalmente o mesmo sentido do campo eléctrico e da corrente, e é
constante ao longo semicondutor, tal como está representado na seguinte figura:
d) Em semicondutores dopados a concentração intrínseca é geralmente várias ordens de
grandeza inferior à concentração de impurezas, para o cálculo da concentração
intrínseca à temperatura ambiente é válida a seguinte fórmula:
ni  B  T  
2
ni 
3

Eg
k T
cm 
6


para o silício:
BSi  2.48 1031 K 3cm 6 e EgSi   1.1 eV 
considerando
T  27º C  300.15 K e
B  T3  


Eg
k T


k  8.62  10-5 eV  K 1
2.48  1031  300.15  
ni 
3

1.1
8.6210- 5 300.15


 

ni  1.5  1010 cm 3  1.5  1016 m 3
Como a concentração de impurezas é 106 [cm-3] temos que:
p
1016

 6.66  105  10 4
ni 1.5  1010

p  10 4  ni
e) A velocidade média de uma lacuna dentro de um semicondutor é proporcional ao campo
eléctrico aplicado, sendo a mobilidade a constante de proporcionalidade. O seu valor é
dado pela seguinte fórmula:



v   p  E  0.048  1000 u x m  s 1  48 u x m  s 1

, pois
 p  0.048 m2  V 1s 1 
A lacuna desloca-se no sentido do terminal negativo da fonte, ou seja no sentido do
versor u x . O tempo médio que a lacuna demora a percorrer o cristal é dado pela
fórmula da velocidade média:
v
2.
s
s
 t 
t
v
, e portanto
tmédio 
c
 2.083  10- 4 s 
48
O processo de geração de pares electrão-lacuna é provocado pela destruição de ligações
covalentes, quer devido ao efeito fotoeléctrico, quer devido à agitação térmica. Desde que
lhe seja fornecida a energia necessária para passar para a banda de energia de condução,
um electrão numa ligação covalente pode sair da influência do(s) núcleo(s), tornando-se
assim num electrão livre. Paralelamente, a falta desse electrão na ligação atingida origina
uma lacuna. Sob a influência de um campo eléctrico estas duas cargas móveis movem-se em
sentidos opostos, sendo o seu efeito conjugado no transporte de carga, ou seja, somandose a sua contribuição em termos de corrente.
A recombinação é o processo oposto, i.e. uma lacuna e um electrão livre chocam e o
electrão livre ocupa o espaço vago na orbital carente. Quando o electrão livre é apanhado
pela lacuna liberta energia, dado que passa para a banda de energia de valência. A
consequência deste choque é a perda de ambas as cargas móveis, o que em média não é
muito significativo dado que a taxa de recombinação é relativamente reduzida.
Em semicondutores dopados, a variação da temperatura pouco afecta a concentração dos
portadores de carga maioritários, neste caso das lacunas. A mobilidade aumenta com a
diminuição da temperatura devido à redução da agitação térmica.
II. Díodos
1.
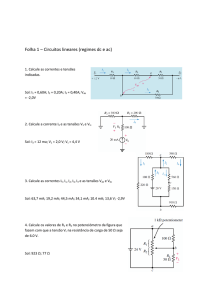
a) O díodo está polarizado inversamente, uma vez que o sentido da corrente no díodo
seria da zona N para a zona P. Como o valor da fonte de tensão é inferior ao módulo da
tensão de Zener é de esperar que o díodo esteja na zona de corte.
Aplicando o método de redução ao absurdo, temos que:
Hipótese (1): o díodo está em condução
sendo assim sabe-se que VD = Vth = 0.7V, e como VR = R.ID
VD  Vg  VR  VD  Vg  R  I D  I D  
Vg  VD
R
 0.57mA
Mas se ID < 0 então o díodo não pode estar em condução (contraria a hipótese)
Hipótese (2): o díodo está na zona de Zener
sendo assim sabe-se que VD = VZ = -7V
VD  Vg  VR  I D  
Vg  VD
R
 ID  
57
 0.2mA
R
Mas se ID > 0 então o díodo não pode estar na zona de Zener (contraria a
hipótese)
Finalmente pode confirmar-se pela analise do circuito que o diodo está cortado:
Hipótese: o díodo está na zona de corte
sendo assim sabe-se que ID  0, e portanto VR = ID.R  0
VD  Vg  VR  Vg  5V
consequentemente VD < 0 o que confirma a hipótese que o diodo está cortado
b) A figura seguinte representa a distribuição de carga no díodo quando lhe é aplicada
uma polarização inversa. O campo eléctrico aplicado vai atrair muita da carga móvel
para as extremidades do díodo, despovoando assim a zona central do dispositivo. Deste
modo, a zona de junção alarga consideravelmente e grande parte das impurezas nesta
zona estão ionizadas, este iões estão assinalados na figura como carga fixa. Não há
passagem de carga móvel pela zona de junção e consequentemente a passagem de
corrente é desprezavel. A barreira de potencial aumenta consideravelmente. A tensão
aplicada ao díodo não é, no entanto, suficiente para que o díodo entre na zona de Zener
e possa haver condução no sentido inverso.
c) No caso de o valor da fonte ser aumentado para 15V, o díodo entra claramente na zona
de condução inversa ou de disrupção. Existem dois efeitos que vão determinar o
funcionamento do díodo. O efeito de Zener corresponde a ser vencido o potencial de
barreira da junção, de modo que a carga móvel pode saltar de um lado para o outro,
apesar da largura da zona de junção. Ou seja, pode dizer-se que a partir de um
determinado potencial (denominado tensão de Zener – VZ) um electrão pode saltar
directamente da zona p para a zona n. O efeito de avalanche está também relacionado
com a zona de disrupção do dispositivo, e consiste no facto de a partir de um dado
potencial, a energia associada ao movimento da carga móvel ser suficientemente
elevada para provocar a destruição de ligações covalentes devido aos choques desta
com a estrutura. Estes choques levam à geração de novos pares lacuna-electrão que por
sua vez provocam novos choques resultando numa reacção em cadeia, que se propaga
como uma bola de neve. A conjunção destes efeitos faz com que o díodo apresente uma
condutividade quase infinita nesta zona, ou seja, permite que tenha grandes variações
de corrente com pequeníssimas variações de tensão. Em díodos de Zener o valor destes
potenciais é muito bem controlado o que faz com que sejam muito usados como
reguladores de tensão contínua.
d) A seguinte figura representa a característica ID(VD) do díodo (incluindo a zona de
Zener) e as rectas de carga correspondentes à equação da malha, para cada um dos
valores de Vg .
 VVD

I D  I S    T  1




ID  
V g  VD
R
(característica do díodo excepto zona de Zener)
(equação da malha do circuito)
No caso de Vg=5V são válidas as expressões anteriores. A equação não-linear que
define o ponto de intersecção das duas equações anteriores determina o ponto de
funcionamento (PFR), ou seja, o ponto onde a recta de carga intersecta a
característica ID(VD) do díodo. Deste modo podem obter-se valores aproximados da
corrente e da tensão aos seus terminais:
1ª iterada (hipótese ID0  0)
I D1
 VVD 0

 I S   T  1  10 15 A




em que V D1   Vg  R  I D 0  5V
2ª iterada (hipótese ID1  -10-15A, VD1  -5V)
I D2
 VVD1

 I S   T  1  10 15 A




em que V D2   Vg  R  I D1  4.99(9)V
Assim, e dado que os valores da tensão VD e da corrente ID estabilizaram, os seguintes
valores estão muito próximos dos valores correctos: VD-4.99999V e ID-10-15A.
No caso de Vg=15V é apenas válida a equação da malha, ou seja, a recta de carga. Para
definir o comportamento do díodo podemos usar a forma nais simples de o caracterizar
na zona de Zener, que é o modelo constante: VD = VZ. A intersecção das duas equações
determina o PFR, obtendo-se os seguintes valores:
VD  VZ  7V

V D   Vg  R  I D
V D   7V

 V g  VD

15V  7V
ID 

 0.8mA

R
10k

Neste caso, os valores de VD e ID são aproximadamente: VD-7V e ID-0.8mA.
2.
a) A análise do circuito permite concluir que as hipóteses válidas para o funcionamento
dos díodos em cada uma das combinações das tensões de entrada são as seguintes:
VA
VB
DA
DB
I
VO
0V
0.4V
ON
OFF
1.467mA
0.6V
0V
4.5V
ON
OFF
1.467mA
0.6V
4.9V
0V
OFF
ON
1.467mA
0.6V
5V
4.7V
OFF
OFF
0A
5V
b) A tabela representa igualmente os valores da tensão de saída e da corrente na
resistência que resultam da análise do circuito. A porta lógica representada é um AND.
III. Transístores de Junção Bipolar (TJBs)
1. A seguinte figura representa fisicamente um transístor de junção bipolar do tipo npn:
O transístor de junção bipolar pnp é formado a partir da combinação de duas zonas p e
uma zona n, tal como está representado na figura. A união destes pedaços de
semicondutor cria duas junções: a junção emissor-base e a junção colector-base. A zona do
emissor é geralmente mais dopada que o colector, sendo também geralmente mais pequena.
A zona intermédia é designada como base, e é geralmente uma zona relativamente
estreita. Em termos de funcionamento, há quatro zonas distintas de funcionamento a que
correspondem quatro comportamentos distintos e tipos de polarização das zonas de
junção. A tabela seguinte resume estas zonas:
VEB
VCB
JunçãoEB
JunçãoCB
IC
VCE
Saturação
 Vth
 Vth
directa
directa
IC  βF.IB
|VEC |  0.1 V
ZAD
 Vth
 Vth
directa
inversa
IC = βF.IB
VEC  0.1 V
ZAI
 Vth
 Vth
inversa
directa
IC = (βR-1).IB
VEC  -0.1 V
Corte
 Vth
 Vth
inversa
inversa
IC  IB  0
Uma das principais aplicações de um transístor bipolar é a de ser utilizado em montagens
de amplificação (e.g. amplificadores de audio). Neste tipo de aplicação a zona privilegiada
de utilização é a zona activa directa (ZAD).
Quando o transístor está na ZAD (situação representada na figura anterior) o princípio de
funcionamento deriva da injecção de lacunas no emissor, que, devido à polarização directa
da junção de emissor-base, se deslocam para a base do transístor. Assim, o aumento
significativo de portadores minoritários de tipo p na base (tipo n) provoca que devido ao
efeito de difusão, a maioria destas lacunas seja arrastada para o colector. Esta relação
traduz-se no coeficiente βF, que relaciona a corrente de colector com a corrente de base,
sendo válida a equação IC=βF.IB.
Na zona de saturação ambas as junções do transístor estão directamente polarizadas,
portanto a diferença de potencial entre o colector e o emissor é quase nula, isto porque
VEC=VEB+VBC e tanto VEB como VCB são aproximadamente iguais à tensão de threshold (e.g.
entre 0.6V e 0.7V). Como VEB é ligeiramente superior a VCB, VEC é geralmente inferior a
0.1V ou 0.2V. Nesta zona a quantidade de carga que é recolhida pelo colector é bastante
inferior e portanto IC  βF.IB.
Na zona de corte ambas as junções do transístor estão inversamente polarizadas, pelo que
não há corrente no transístor. A diferença de potencial entre o colector e o emissor é
imposta pelo circuito exterior e pode ser positiva ou negativa.
A ZAI corresponde à utilização do pnp com o emissor trocado com o colector, e é uma
zona de funcionamento muito pouco utilizada, essencialmente devido ao facto de o ganho
de corrente ser muito inferior ao que se obtém na ZAD. O princípio de funcionamento
nesta zona é relativamente análogo ao da zona activa directa, mas a injecção de electrões
livres acontece no colector, e a recolha é feita no emissor. A relação entre a corrente de
colector e a corrente de base, que é dada pelo coeficiente β R é muito inferior a βF (pelo
menos uma ordem de grandeza abaixo, i.e. pelo menos dez vezes menor).
2.
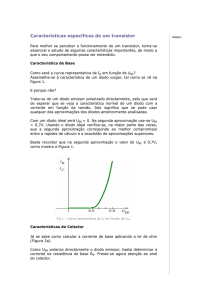
a) A determinação do ponto de funcionamento em repouso (PFR) corresponde ao cálculo
das correntes e tensões do transístor em regime estático (ou seja, em DC).
Sendo assim, basta calcular IC, IB, IE, VBE, VCE e VBC. Aplicando o teorema da
sobreposição, anulam-se as fontes de sinal e calculam-se os valores DC de todas as
correntes e tensões no dispositivo. Partindo da hipótese que o TJB está na ZAD, e
assumindo que F = 110 e VBE(ON) =Vth = 0.6V temos que:
 I E   F  1  I B
I E 
 
V  R  I  V
B
B
BE( ON )  RE  I E
 B
VB  RB  I B  VBE( ON )  RE   F  1  I B
I E 

VB  Vth

I 
B

RB  RE   F  1

I E 
 I  6.68 mA

 E
4V  0.6V
I 
I  60.178 A
B

1k  500  111  B

I C   F  I B
 I  6.62 mA
 I  6.62 mA
 C
 C

VC  RC  I C  VCE  RE  I E
VCE  VC  RC  I C  RE  I E
VCE  6.73V
Ambas as equações confirmam a hipótese de o TJB estar na ZAD, portanto não está na
zona de saturação.
b) O valor da transcondutância do TJB na ZAD é dado pela seguinte fórmula:
gm 
I C
VBE
VBE


 I S   VT

 
VBE


VBE
 I   VT
IC
 S

 40  I C  264.8 mS
VT
25mV
O modelo incremental equivalente (modelo π) do transístor quando este é utilizado na
ZAD está representado na seguinte figura:
Substituindo o TJB pelo seu modelo equivalente na montagem de emissor comum
degenerado representada no enunciado, e anulando todas as fontes DC obtém-se o
modelo incremental da montagem representado na figura seguinte. Sabe-se que são
válidas as equações: ic = o.ib, ie = (o+1).ib e r = o/gm  415.4.
iE  iB  iC
iE   O  1  iB

i  v  v  g m  iC  
B
iC   O  iB

r
O
O

O cálculo do ganho incremental de tensão deriva simplesmente da análise do circuito:
iE  195A
iE   O  1  iB

vi
 

i

 1.757A
v

R

i

r

i

R

i
B
B
B

B
E
E
 i

RB  r  RE   F  1

v 
r
r  RB   O  1  RE
iC  g m  v  vo   g m
 vi
r
r  RB   O  1  RE
 vi  RC 
vo
 2.9
vi
c) A principal vantagem da montagem de emissor comum degenerado é a facilidade na
determinação do ganho, dado que fica apenas dependente de uma relação entre
componentes passivos. Desta forma, é relativamente fácil assegurar grande precisão
na determinação do ganho de tensão, especialmente em circuitos integrados. No caso
da montagem de emissor comum o ganho depende da transcondutância do TJB, e
portanto varia com muita facilidade com a temperatura e com a precisão da corrente
de polarização (Ic). O facto de o valor da transcondutância ser geralmente sensível a
variações processuais também prejudica a determinação do ganho.
As principais desvantagens são a utilização de mais um componente, a ligeira diminuição
no ganho incremental de tensão e diminuição da margem de tensão disponível para que o
TJB esteja na ZAD.
IV. Transístores de Efeito de Campo (MOSFETs)
1. A figura seguinte representada uma implementação física de um transístor de efeito de
campo (TEC) do tipo PMOS:
O princípio de funcionamento deste TEC consiste na formação ou não de um canal entre o
dreno e a source. A aplicação de uma tensão negativa entre a gate e a source do
dispositivo gera um campo eléctrico que atrai as lacunas disponíveis na source e no dreno.
Assim, a partir de uma determinada tensão (denominada tensão de limiar ou de threshold),
a concentração de carga móvel na zona que está sob a gate, é suficiente para assegurar
uma conductividade elevada entre a source e o dreno. Ou seja, pode considerar-se que o
canal está formado. Para tensões inferiores (em módulo) a este limiar, o canal não está
formado e o TEC apresenta uma conductividade quase nula entre dreno e source, nesta
situação considera-se que o transístor está cortado. Tal como acontece no NMOS, a gate
está separada do canal por uma fina película de dióxido de silício, pelo que a corrente de
gate é nula (da ordem de 10-15A).
O TEC tem duas zonas de condução distintas, uma em que a secção vertical do canal é
aproximadamente rectangular, e que corresponde a ambas as polarizações VSG e VDG
estarem directamente polarizadas – denominada zona linear ou de tríodo. Na outra zona, a
tensão VDG é inferior ao limiar de tensão Vth pelo que o canal estrangula do lado do dreno
sendo a secção do canal aproximadamente triangular – zona activa (ZA) ou zona de
saturação. O seguinte quadro resume as zonas de funcionamento do TEC (PMOS) e as
equações válidas em cada caso.
VSG
ID
VDG
Linear
(ou de tríodo)
 Vth
 Vth
ID  kp
ZA
(ou saturação)
 Vth
 Vth
ID 
Corte
 Vth
 Vth
ID  0
W
L
VSD
2

V 
 VSG  Vth   VSD  SD  VSD  VSG  Vth
2 

kp W
2
  VSG  Vth 
2 L
VSD  VGS  Vth
Este dispositivo é perfeitamente simétrico, i.e. não há distinção física entre o dreno e a
source. Assim a identificação do dreno e da source depende do circuito no qual está
inserido, ou seja, a corrente que entra pelo source (e que sai pelo dreno) é sempre positiva.
Na situação em que VSG  Vth e VDG  Vth o dreno e a source estão trocados e o TEC está na
na zona activa (ZA), sendo o seu funcionamento exactamente análogo.
2. Considerando a montagem de source comum representada no enunciado:
a) Dado que o transístor NMOS está na zona activa, a correntes DC que estabelece o PFR
do TEC é dada por:
ID 
kn W
2
  VGS  Vth 
2 L
 ID 
3  103
2
 1.5  0.6  1.215 mA
2
Assim, para que a tensão média na saída seja 6V, é necessário assegurar que V DS=6V.
Assim, o valor máximo de RD que pode ser utilizado sem que o TEC entre na zona de
tríodo é dado pela seguinte fórmula:
VDS  VDD  I D  RD  6V
 6V  12V  I D  RD  RD 
6V
 4.94 k
ID
Os valores de tensão e corrente que estabelecem o PFR do dispositivo são:
I G  0 , VDS  6V ,
VDS  VGS  Vth  6V  0.9V  ( ZA)
I D  1.215 mA ,
b) O valor da transcondutância do transístor neste circuito é dado pela seguinte equação:
gm 
I D
VGS
k W
2
  n   VGS  Vth  
2 L
  k  W V  V   2.7 mS
 
n
GS
th
VGS
L
A seguinte figura representa o modelo incremental do TEC.
O modelo incremental da montagem deriva facilmente deste, e está representado na
seguinte figura:
O cálculo do ganho incremental de tensão deriva simplesmente da análise do circuito:
iO  g m  v gs  vO   g m  v gs  RD

vO
  g m  RD  13.34
v gs
c) Seria de esperar que o osciloscópio apresente os seguintes sinais (atenção às escalas):
3. As características I D (VDS ) para VGS constante estão representadas na figura seguinte:
A parábola que define a separação entre a zona linear e a zona activa resulta da conjunção das
duas equações seguintes, i.e. é definida pelos pontos da característica em que VDS=VGS-Vth .
VDS  VGS  Vth
kn W

2
  VDS
 I  k n  W  V  V 2  I D 
2 L
D
GS
th


2 L
Outra forma de o demonstrar seria:
VDS  VGS  Vth
W

2
 I  k  W  V  V   V  VDS   I D  k n 
L
 GS

n
th
DS
 D
L 
2 

2

V  k W
2
 VDS   VDS  DS   n   VDS
2  2 L
