Prova 1

582807344
Criado por John Wisbeck
1
Universidade Federal do Rio Grande do Sul
Escola de Engenharia
Departamento de Engenharia Elétrica
Eletricidade A ENG04474
Prova 1
Nome________________________________ Matrícula_________
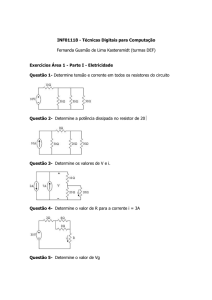
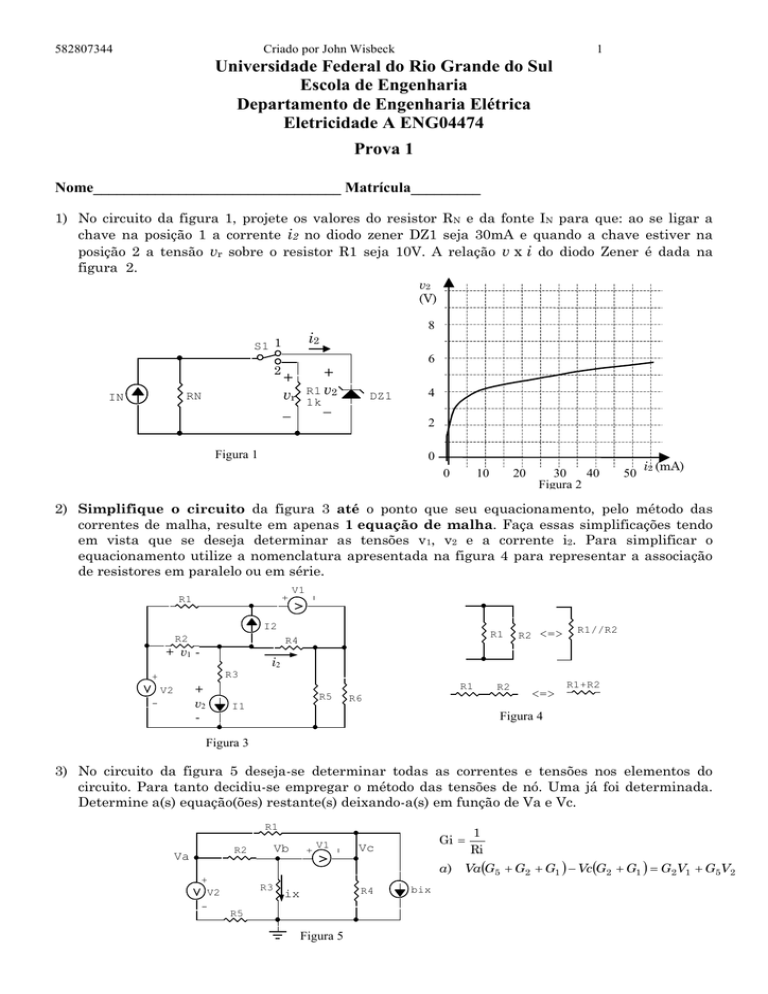
1) No circuito da figura 1, projete os valores do resistor RN e da fonte IN para que: ao se ligar a
chave na posição 1 a corrente i2 no diodo zener DZ1 seja 30mA e quando a chave estiver na
posição 2 a tensão vr sobre o resistor R1 seja 10V. A relação v x i do diodo Zener é dada na
figura 2.
v2
(V)
S1 1
2
RN
IN
8
i2
6
+
+
vr
_
R1 v2
1k
DZ1
_
4
2
Figura 1
0
0
10
20
30
40
Figura 2
50
i2 (mA)
2) Simplifique o circuito da figura 3 até o ponto que seu equacionamento, pelo método das
correntes de malha, resulte em apenas 1 equação de malha. Faça essas simplificações tendo
em vista que se deseja determinar as tensões v1, v2 e a corrente i2. Para simplificar o
equacionamento utilize a nomenclatura apresentada na figura 4 para representar a associação
de resistores em paralelo ou em série.
+
-
V1
R1
I2
R2
R1
R4
+ v1 -
R2 <=>
R1//R2
i2
R3
+
R1
+
v2
-
V2
-
R5
I1
R6
R2
<=>
R1+R2
Figura 4
Figura 3
3) No circuito da figura 5 deseja-se determinar todas as correntes e tensões nos elementos do
circuito. Para tanto decidiu-se empregar o método das tensões de nó. Uma já foi determinada.
Determine a(s) equação(ões) restante(s) deixando-a(s) em função de Va e Vc.
Va
+
V2
-
V1
-
Vb
R2
+
R1
Gi 
Vc
1
Ri
a) Va G5  G2  G1   VcG2  G1   G2V1  G5V2
R3
R4
ix
R5
Figura 5
bix
582807344
Criado por John Wisbeck
2
4) No circuito da figura 6 determine a tensão vx, sabendo que a relação vxi do bipolo B, seguindo a
convenção passiva, é v=(2)i, onde  é a freqüência angular da corrente ou tensão senoidal no
bipolo. Justifique a técnica de solução escolhida em detrimento das outras técnicas.
-
3sen(10t) B
4sen(5t)
+
10
+ vx Figura 6
5) No circuito da figura 7 projete os valores de R1 e R4 para que o equivalente de Thevenin visto
pelos terminais a e b seja o indicado na figura 8. Para tanto:
a) Utilizando o método das correntes de malha, determine o valor de Rth como função de R1 e R4.
b) Utilizando o método das correntes de malha, determine o valor de Vth como função de R1 e R4.
c) A partir das equações em a) e b) projete os valores de R1 e R4 para Vth=11,5V e Rth=100.
R1
a
Rth
+
ib
500
23ib
10V
R4
-
a
Vth
+
b
50
b
Figura 7
Figura 8