Folha 1 – Circuitos lineares (regimes dc e ac)

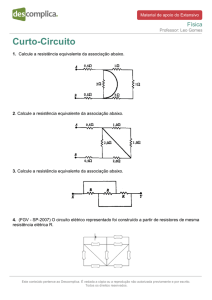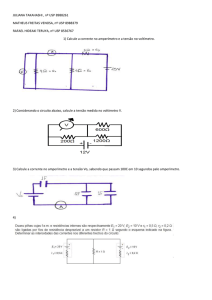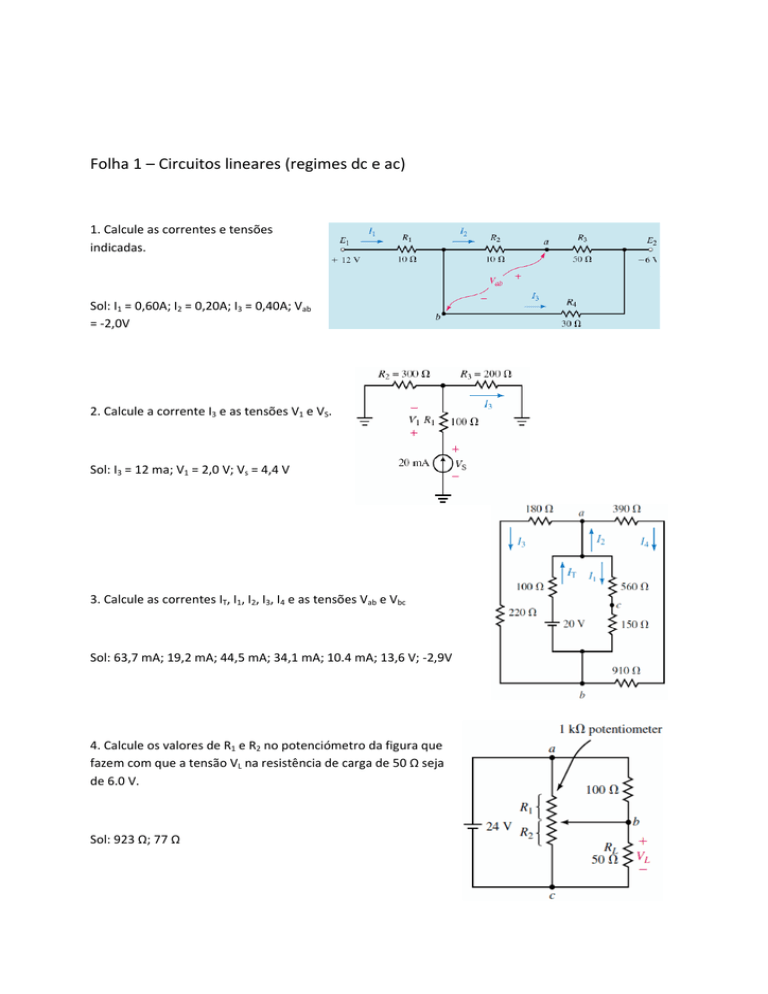
 Folha 1 – Circuitos lineares (regimes dc e ac) 1. Calcule as correntes e tensões indicadas. Sol: I1 = 0,60A; I2 = 0,20A; I3 = 0,40A; Vab = ‐2,0V 2. Calcule a corrente I3 e as tensões V1 e VS. Sol: I3 = 12 ma; V1 = 2,0 V; Vs = 4,4 V 3. Calcule as correntes IT, I1, I2, I3, I4 e as tensões Vab e Vbc Sol: 63,7 mA; 19,2 mA; 44,5 mA; 34,1 mA; 10.4 mA; 13,6 V; ‐2,9V 4. Calcule os valores de R1 e R2 no potenciómetro da figura que fazem com que a tensão VL na resistência de carga de 50 Ω seja de 6.0 V. Sol: 923 Ω; 77 Ω 5. Calcule as correntes I1 e I2. Sol: I1 = 400 µA; I2 = 500 µA 6. Utilize o método dos nós para calcular as tensões dos nós. Sol: ‐6,73V; 1,45V 7. Calcule a corrente I2 e a tensão Vab utilizando o método das malhas. Sol: 3,26 A; ‐13,89 V 8. Calcule a corrente I e a potência consumida pela fonte comandada. Sol: 2 A; 560 W 9. Calcule a potência que cada fonte está a fornecer ou a absorver no circuito. Verifique que a potência fornecida é igual à potência absorvida. 10. Calcule a corrente i utilizando o teorema da sobreposição. Considere R1 = 5 Ω, R2 = 10 Ω, Vs = 10 V e Is= 3 A. Sol: 1,667 A 11. Utilize o teorema da sobreposição para calcular VL. Sol: 9,880º V 12. Calcule vab, sem simplificar o circuito, considerando: (a) k = 0; (b) k = 0,01. Sol: ‐100 V; ‐111,1 V 13. Calcule iL, utilizando o método dos nós, se: (a) α = 0,9; (b) α = 0. Sol: 0,08597vs; 0,04348vs 14. Calcule a impedância de entrada do circuito à frequência de 20 KHz. Sol: 22828.8º  15. Calcule I, VR, VC, e escreva as correspondentes funções sinusoidais se a frequência for 50 Hz. Calcule também a potência média fornecida pela fonte. I  7,581,3º A VR  15081,3º V VC  187,5  8,66º V
Sol: i  10,6sin  314t  81,3º  A vR  212sin  314t  81,3º V
P  1,125kW
16. Utilize o divisor de corrente para calcular iL. Sol: iL  5,18sin  400t  57,1 A
17. Utilize duas vezes o divisor de corrente para calcular IL. Sol: I L  6,85  7º A 18. Calcule a impedância de entrada do circuito à frequência de 50 kHz. Sol: 2,83  135º S 19. Calcule Iin e IL. Sol:
I in  27,521,3º A I L  117º A vC  265sin  314t  8,66º  20. Calcule as correntes das malhas (I1 e I2). Sol: I 1  1, 28 85, 5 A
I 2   3  13º A 21. Calcule I utilizando: o método das malhas; o método dos nós. Sol: 63,344 A 22. Calcula as tensões dos nós. Sol: V1  2,07  26,6º V
V2  1,387, 36º V V3  1,55  146º V 23. Calcule V em função de I. Calcule em seguida o valor numérico de V. 

Sol: V  17,2.10 29,5º I
4
V  9,9578,8º V
24. Calcule o equivalente de Thévenin para o circuito à esquerda dos terminais a e b. Considere V1 = 10 V, V2 = 15 V, R1 = 4 Ω, R2 = 6 Ω. Sol: VTh = 12 V; RTh = 2,4 Ω 25. Calcule os equivalentes de Thévenin e de Norton para o circuito à esquerda dos terminais a e b. Utilize‐os para calcular a corrente IL. Sol: VTh = V1 – I2R2 ; ZTh = R1 + R2 ; IN = (V1 – I2R2) / (R1 + R2) ; IL = (V1 – I2R2) / (R1+R2+RL) 26. Calcule o equivalente de Thévenin do circuito. Sol: RTh = 8,8 Ω 27. Calcule o equivalente de Thévenin do circuito à esquerda dos terminais 1 e 2. Considere VA = 4 V, α = 0,25 A/V, R1 = 2 Ω, R2 = 3 Ω. Sol: VTh = 8 V; ZTh = 10 Ω 28. Calcule o equivalente de Norton do circuito exterior a RL. Use‐o para calcular IL. Sol: I N  0,3330º A
Z N  14, 2318, 43º  I L  0,080814,03º A 29. Calcule o equivalente de Norton do circuito exterior a RL. Sol: I N  1,750º mA
Z N  8,57 k  30. Calcule os equivalentes de Thévenin e de Norton do circuito exterior a RL. Sol: VTh = –4,0V; IN = –1,25 mA; ZTh = ZN = 3,2 kΩ 31. Calcule o equivalente de Thévenin do circuito exterior a RL (sugestão: utilize o teorema da sobreposição para simplificar os cálculos). Calcule também a corrente em RL e a potência dissipada por RL. Sol: VTh  1,79153, 43º V
Z Th  17,9  26,56º 
iL  0,0316161,56º mA P  40,0 W