6.1. função derivada derivadas 6 exercícios resolvidos

FUNÇÕES
6
©AREAL EDITORES
PREPARAR O EXAME NACIONAL / MATEMÁTICA A 12
DERIVADAS
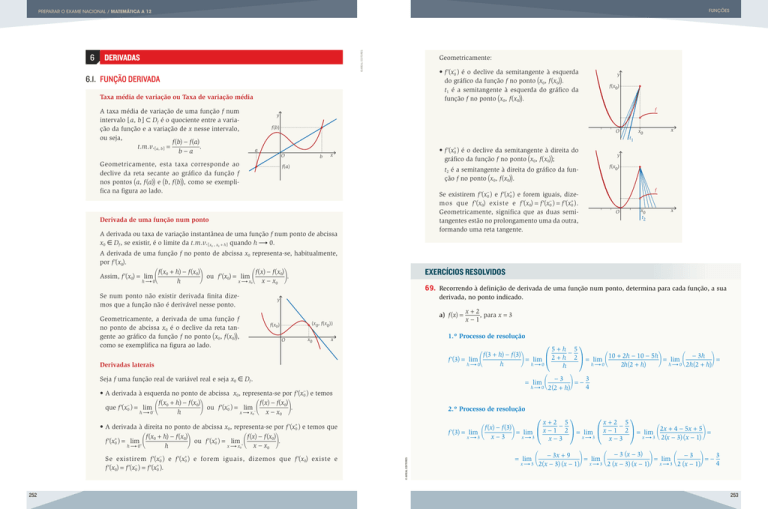
Geometricamente:
•f r1x-0 2 é o declive da semitangente à esquerda
do gráfico da função f no ponto 1x0, f 1x022.
t1 é a semitangente à esquerda do gráfico da
função f no ponto 1x0, f 1x022.
6.1. FUNÇÃO DERIVADA
Taxa média de variação ou Taxa de variação média
A taxa média de variação de uma função f num
intervalo f a, b g ƒ Df é o quociente entre a variação da função e a variação de x nesse intervalo,
ou seja,
f 1b2 - f 1a2
t.m.v. f a, b g =
.
b-a
y
f(b)
f
O
a
O
b
•f r1x+0 2 é o declive da semitangente à direita do
gráfico da função f no ponto 1x0, f 1x022;
x
f(a)
t2 é a semitangente à direita do gráfico da função f no ponto 1x0, f 1x022.
Se existirem fr1x-0 2 e fr1x+0 2 e forem iguais, dizemos que fr1x02 existe e fr1x02 = fr1x-0 2 = fr1x+0 2 .
Geometricamente, significa que as duas semitangentes estão no prolongamento uma da outra,
formando uma reta tangente.
Derivada de uma função num ponto
A derivada ou taxa de variação instantânea de uma função f num ponto de abcissa
x0 å Df , se existir, é o limite da t.m.v. f x , x + h g quando h " 0.
x
x0
y
f(x0)
f
O
x0
t2
x
0
A derivada de uma função f no ponto de abcissa x0 representa-se, habitualmente,
por fr1x02.
f 1x + h2 - f 1x02
f 1x2 - f 1x02
Assim, fr1x02 = lim a 0
b.
b ou fr1x02 = lim a
h"0
x " x0
x - x0
h
Se num ponto não existir derivada finita dizemos que a função não é derivável nesse ponto.
Geometricamente, a derivada de uma função f
no ponto de abcissa x0 é o declive da reta tangente ao gráfico da função f no ponto 1x0, f 1x022,
como se exemplifica na figura ao lado.
EXERCÍCIOS RESOLVIDOS
69.Recorrendo à definição de derivada de uma função num ponto, determina para cada função, a sua
derivada, no ponto indicado.
y
a) f 1x2 =
(x0, f(x0))
f(x0)
O
x0
x
Seja f uma função real de variável real e seja x0 å Df .
h"0
2.º Processo de resolução
-3
3
b=4
2 12 + h2
x+2 5
x+2 5
f 1x2 - f 132
2x + 4 - 5x + 5
x
1
2
x
f'132 = lim a
b = lim °
¢ = lim ° - 1 2 ¢ = lim a
b=
x"3
x-3
x"3
x
"
3
x
"
3
2 1x - 32 1x - 12
x-3
x-3
© AREAL EDITORES
Se existirem fr1x-0 2 e fr1x+0 2 e forem iguais, dizemos que fr1x02 existe e
fr1x02 = fr1x-0 2 = fr1x+0 2.
1.º Processo de resolução
= lim a
•A derivada à esquerda no ponto de abcissa x0, representa-se por fr1x-0 2 e temos
f 1x + h2 - f 1x02
f 1x2 - f 1x02
que fr1x-0 2 = lim - a 0
b.
b ou fr1x-0 2 = lim - a
h"0
x " x0
x - x0
h
•A derivada à direita no ponto de abcissa x0, representa-se por fr1x+0 2 e temos que
f 1x + h2 - f 1x02
f 1x2 - f 1x02
fr1x+0 2 = lim + a 0
b.
b ou fr1x+0 2 = lim + a
h"0
x " x0
x - x0
h
x+2
, para x = 3
x-1
5+h 5
f 13 + h2 - f 132
10 + 2h - 10 - 5h
- 3h
2
f '132 = lim a
b = lim ° + h 2 ¢ = lim a
b = lim a
b=
h"0
h"0
h
"
0
h
"
0
h
1
2
12 + h2
2h
2
+
h
2h
h
Derivadas laterais
252
f(x0)
t1
Geometricamente, esta taxa corresponde ao
declive da reta secante ao gráfico da função f
nos pontos 1a, f 1a22 e 1b, f 1b22, como se exemplifica na figura ao lado.
0
y
= lim a
x"3
- 3 1 x - 32
3
- 3x + 9
-3
b = lim a
b = lim a
b=x
"
3
x
"
3
4
2 1 x - 32 1 x - 12
2 1x - 32 1x - 12
2 1x - 12
253