Escola Secundária de Caneças

Escola Secundária de Caneças
4a Ficha de Matemática (Triângulo de Pascal e Binómio de Newton)
12ºAno
Novembro
Nome ______________________________________________N º _______ Turma _____
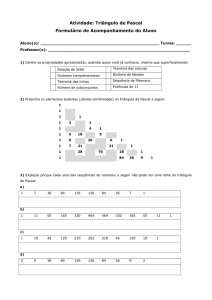
Triângulo de Pascal
1. Complete indicando os valores das seguintes combinações. Qual é a linha 4?
0
C0 ------------------------------- Linha 0------------------------ ....
1
1
C0
2
2
C0
3
2
C1
3
C0
C1 --------------------------- Linha 1--------------------- ....
C1
C2 - --------------------- Linha 2----------------- ....
C2 3C3 ------------------Linha 3------------- ....
3
....
....
....
....
....
....
Propriedades das combinações
No triângulo de Pascal :
 Cada linha começa e acaba sempre em 1, isto é
n
C 0 1
e n C n 1
n
n
 Em cada linha os termos equidistantes dos extremos são iguais: Cp  Cn p , n  p  p  0
 Adicionando dois números consecutivos de uma linha obtém-se o número que na linha seguinte se
n
n
n1
encontra entre eles: Cp  Cp1  Cp1
, n  p 1 .
 O segundo elemento da linha é sempre igual ao número de ordem da linha:
n
C1  n
 A soma de todos os termos da linha de ordem n é 2 n , isto é, um conjunto com n elemento tem
n
exactamente 2 n subconjuntos:

n
Ck  2 n .
k 0
2. Demonstre as quatro primeiras propriedades do triângulo de Pascal
n!
n
Cp 
e a última usando o método de indução matemática.
p ! n  p !
usando a propriedade
3. Os quatro primeiros números de uma certa linha do triângulo de Pascal são 1, 11, 55 e 165
Então os últimos números da linha seguinte são:
(A) 36, 24 e 12
(B) 66, 12 e 1
(C) 220, 66 e 12
(D) 24, 12 e 1
4.
C100  1997C101 é igual a:
1997
(A)
1998
C101
(B)
1996
C100
(C)
1997
C 201
(D)
1998
C100
5. O penúltimo número de uma certa linha do triângulo de Pascal é 10.
Qual é o terceiro número dessa linha ?
(A) 11
(B) 19
(C) 45
(D) 144
(Exame de 98 - 1ª Fase)
6. Considere duas linhas consecutivas do triângulo de Pascal, das quais se reproduzem alguns
elementos:
....
36
a
126
.....
....
120
b
....
O valor de b é (A) 164
(B) 198
(C) 210
(D) 234. (Prova modelo 99)
7. Determine a soma dos números que figuram na 6ª linha do triângulo de Pascal.
8. Determine x sabendo que
100
C39 100Cx
,
x  39 .
9. Resolva, em IN 0 , a equação 15C3 15C4  n5C4 .
10.Se o terceiro elemento de uma certa linha do triângulo de Pascal é 1225, então a probabilidade de
o segundo elemento dessa linha ser 50 é: (A) 0
(B) 0,25
(C) 0,5
(D) 1
11.Numa certa linha do triângulo de Pascal, têm-se os seguintes números consecutivos: x
Qual o valor de x? (A) 1
(B) 326
(C) 625
(D) 2300
300 25
1.
Binómio de Newton
Chama-se Binómio de Newton a toda a expressão do tipo a  b n com a ,b  IR , n  IN0 e a  b  0
O binómio de Newton é tão belo como a Vénus de Milo – o que há é pouca gente a dar por isso.
Fernando Pessoa
12. Complete: a  b  0
a  b 1
a  b 2
a  b 3
n
Binómio de Newton: a  b  n nC0a nb0  nC1a n 1b   nCn a 0bn   nCk a n  k bk
k 0
Relativamente ao desenvolvimento de a  b  n pode afirmar-se que:
 Tem n+1 parcelas.
 Os coeficientes de cada monómio são os termos da linha n do triângulo de Pascal.
 Os expoentes de a decrescem de n a 0 e os de b crescem de 0 a n.
 A soma dos expoentes de a e de b é sempre igual a n.
 O Termo geral do desenvolvimento do binómio de Newton: Tp1  nCp a n p b p .
13 - Usando a fórmula do Binómio de Newton, determine o desenvolvimento de:
6
5
1
4
6

13.1  x  y 
13.2  2a  
13.3  x  2
13.4 2  3

2


13.5  h 

3

h
3
y

13.6  x 2  

x
5

13.7 2  i  5 i é a unidade imaginária
R: -38+41i
10
 1 x
14. Determine o 7º termo do desenvolvimento  2   .
x
2
8
 2
a
 , a0
15. Escreva o termo médio do desenvolvimento 


b
2


 b  0.
6
a

16. Considere o desenvolvimento   3b 
2

16.1 Indique o número de termos do desenvolvimento.
16.2 Determine o termo médio do desenvolvimento.
R: 7
135 3 3
a b
R:
2
17. Um dos termos do desenvolvimento de   e n é 127 7 e3 . Indique o valor de n.
Bom trabalho
R:10