Cálculo da carga aplicada

510BZ
Cálculo da carga aplicada
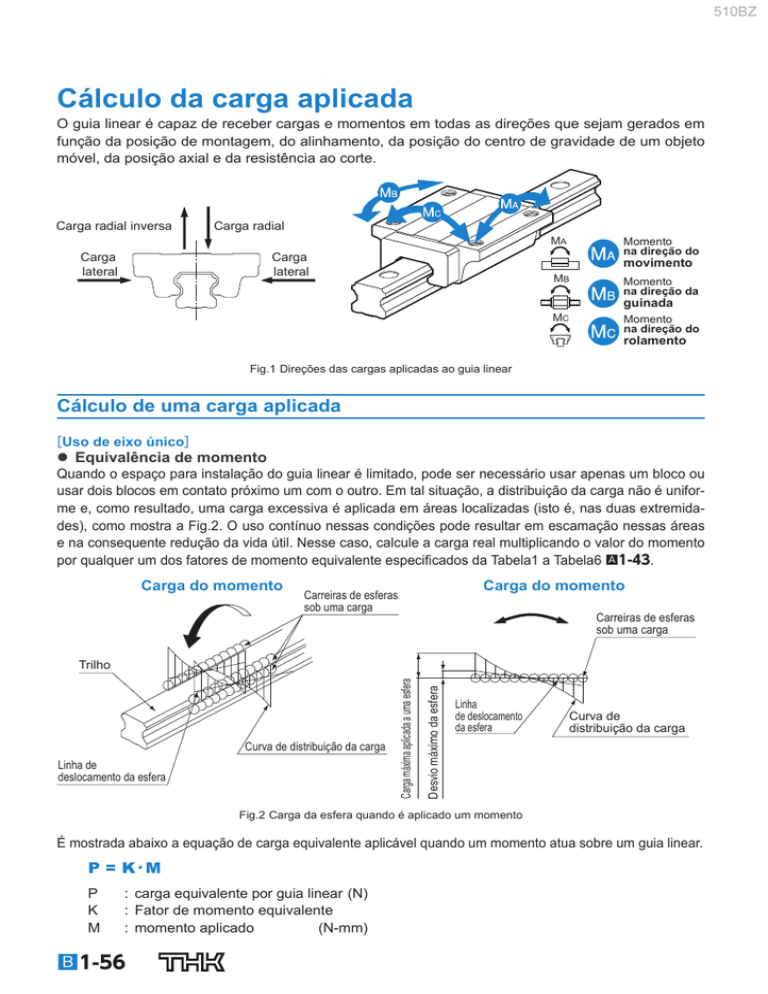
O guia linear é capaz de receber cargas e momentos em todas as direções que sejam gerados em
função da posição de montagem, do alinhamento, da posição do centro de gravidade de um objeto
móvel, da posição axial e da resistência ao corte.
Carga radial inversa
Carga radial
MA
Carga
lateral
Carga
lateral
Momento
na direção do
movimento
MB
Momento
na direção da
guinada
MC
Momento
na direção do
rolamento
Fig.1 Direções das cargas aplicadas ao guia linear
Cálculo de uma carga aplicada
[Uso de eixo único]
 Equivalência de momento
Quando o espaço para instalação do guia linear é limitado, pode ser necessário usar apenas um bloco ou
usar dois blocos em contato próximo um com o outro. Em tal situação, a distribuição da carga não é uniforme e, como resultado, uma carga excessiva é aplicada em áreas localizadas (isto é, nas duas extremidades), como mostra a Fig.2. O uso contínuo nessas condições pode resultar em escamação nessas áreas
e na consequente redução da vida útil. Nesse caso, calcule a carga real multiplicando o valor do momento
por qualquer um dos fatores de momento equivalente especificados da Tabela1 a Tabela6 A1-43.
Carga do momento
Carga do momento
Carreiras de esferas
sob uma carga
Carreiras de esferas
sob uma carga
Carga máxima aplicada a uma esfera
Curva de distribuição da carga
Linha de
deslocamento da esfera
Desvio máximo da esfera
Trilho
Linha
de deslocamento
da esfera
Curva de
distribuição da carga
Fig.2 Carga da esfera quando é aplicado um momento
É mostrada abaixo a equação de carga equivalente aplicável quando um momento atua sobre um guia linear.
P = K•M
P
K
M
: carga equivalente por guia linear (N)
: Fator de momento equivalente
: momento aplicado
(N-mm)
B1-56
510BZ
Diagrama de seleção
Cálculo da carga aplicada
 Fator equivalente
Fatores equivalentes para o momento MA
PR=KAR•MA
Equivalente na direção radial
PL=KAL•MA
Equivalente na direção radial inversa
Fig.3 Fatores equivalentes para o momento MA
Fatores equivalentes para o momento MA
Fator equivalente
na direção radial
KAR=
C0
MA
Fator equivalente na
direção radial inversa
KAL=
C0L
MA
C0
C0L
=
=1
KAR•MA KAL•MA
Fatores equivalentes para o momento MB
PT=KB•MB
Equivalente na direção lateral
PT=KB•MB
Equivalente na direção lateral
Fig.4 Fatores equivalentes para o momento MB
Fatores equivalentes para o momento MB
C0T
Fator equivalente
KB=
nas direções laterais
MB
C0T
=1
KB•MB
B1-57
Guia Linear
Como a carga nominal é equivalente ao momento permitido, o fator equivalente a ser multiplicado
durante a equalização dos momentos MA, MB e MC para a carga aplicada por bloco é obtido pela divisão das cargas nominais nas direções correspondentes.
Com modelos que não sejam dos tipos de carga uniforme nas quatro direções, contudo, as especificações de carga nas quatro direções diferem umas das outras. Sendo assim, os valores de fator
equivalente para os momentos MA e MC também serão diferentes caso a direção seja radial ou radial inversa.
510BZ
Fatores equivalentes para o momento MC
PR=KCR•MC
Equivalente na direção radial
PL=KCL•MC
Equivalente na direção radial inversa
Fig.5 Fatores equivalentes para o momento MC
Fatores equivalentes para o momento MC
Fator equivalente
na direção radial
KCR=
C0
MC
Fator equivalente na
direção radial inversa
KCL=
C0L
MC
C0
C0L
=
=1
KCR•MC KCL•MC
C0
C0L
C0T
PR
PL
PT
:
:
:
:
:
:
B1-58
carga nominal estática (direção radial)
carga nominal estática (direção radial inversa)
carga nominal estática (direção lateral)
carga calculada (direção radial)
carga calculada (direção radial inversa)
carga calculada (direção lateral)
(N)
(N)
(N)
(N)
(N)
(N)
510BZ
Diagrama de seleção
Cálculo da carga aplicada
Exemplo de cálculo
Quando um bloco é usado
N.º do modelo: SSR20XV1
N.º 3
N.º 4
N.º 2
N.º 1
ℓ1
Guia Linear
Aceleração gravitacional g=9,8 (m/s2)
Massa m = 10 (kg)
ℓ1=200（mm）
ℓ2=100（mm）
ℓ2
m
m
Fig.6 Quando um bloco é usado
N.º 1
N.º 2
N.º 3
N.º 4
P1=mg+KAR1•mg•ℓ1+KCR•mg•ℓ2=98+0,275×98×200+0,129×98×100 = 6.752 (N)
P2=mg‒KAL1•mg•ℓ1+KCR•mg•ℓ2=98‒0,137×98×200+0,129×98×100 = ‒1.323 (N)
P3=mg‒KAL1•mg•ℓ1‒KCL•mg•ℓ2=98‒0,137×98×200‒0,0644×98×100 = ‒3.218 (N)
P4=mg+KAR1•mg•ℓ1‒KCL•mg•ℓ2=98+0,275×98×200‒0,0644×98×100 = 4.857 (N)
Quando dois blocos são usados próximos um do outro
Nº do modelo: SVS25R2
Aceleração gravitacional g=9,8 (m/s2)
Massa m = 5 (kg)
ℓ1=200（mm）
ℓ2=150（mm）
N.º 3
N.º 4
N.º 2
N.º 1
ℓ1
ℓ2
m
m
Fig.7 Quando dois blocos são usados próximos um do outro
N.º 1 P1=
mg
49×150
mg•ℓ2 49
+0,0188×49×200+0,0814×
=507,9 (N)
+KAR2•mg•ℓ1+KCR•
=
2
2
2
2
N.º 2 P2=
mg
49×150
mg•ℓ2 49
–KAL2•mg•ℓ1+KCR•
=
–0,0158×49×200+0,0814×
=168,8 (N)
2
2
2
2
N.º 3 P3=
49×150
mg
mg•ℓ2 49
–KAL2•mg•ℓ1–KCL•
=
–0,0158×49×200–0,0684×
=–381,7 (N)
2
2
2
2
N.º 4 P4=
49×150
mg
mg•ℓ2 49
+KAR2•mg•ℓ1–KCL•
=
+0,0188×49×200–0,0684×
=–42,6 (N)
2
2
2
2
Nota1) Como uma guia linear usada em instalação vertical recebe somente uma carga de momento, não há necessidade
de aplicar uma força de carga (mg).
B1-59
510BZ
[Uso de eixo duplo]
 Definição das condições
Defina as condições necessárias para calcular a carga aplicada do sistema linear e a vida útil em horas.
As condições consistem nos seguintes itens.
(1) Massa: m (kg)
(2) Direção da carga de trabalho
(3) Posição do ponto de trabalho (por exemplo, centro de gravidade): ℓ2, ℓ3, h1(mm)
(4) Posição axial: ℓ4, h2(mm)
(5) Organização Arranjo do sistema linear: ℓ0, ℓ1(mm)
(Nº de unidades e eixos)
(6) Diagrama da velocidade
Velocidade:V (mm/s)
Constante de tempo: tn (s)
Aceleração: n(mm/s2)
V
(αn = tn
)
(7) Ciclo de trabalho
Número de movimentos alternados por minuto: N1(min-1)
(8) Comprimento do curso: ℓs(mm)
(9) Velocidade média: Vm(m/s)
(10) Vida útil necessária em horas: Lh(h)
ℓ1
ℓ2
ℓ3
mg
h2
ℓ4
h 1 ℓ0
Velocidade (mm/s)
Aceleração da gravidade g=9,8 (m/s2)
Ciclo de trabalho
V
tn
tn
ℓS
Diagrama da velocidade
Fig.8 Condição
B1-60
t1
（s）
（mm）
510BZ
Diagrama de seleção
Cálculo da carga aplicada
 Equação de carga aplicada
A carga aplicada ao guia linear varia de acordo com a força externa, como a posição do centro de
gravidade de um objeto, a posição axial, a inércia gerada pela aceleração/desaceleração durante
movimento ou parada, e a força de corte.
Para selecionar um guia linear, é necessário obter o valor da carga aplicada e considerar essas
condições.
Guia Linear
Calcule a carga aplicada ao guia linear nos exemplos 1 a 10 mostrados abaixo.
m
: Massa
(kg)
ℓn
: Distância
(mm)
: Força externa
(N)
Fn
: carga aplicada (direção radial/radial inversa) (N)
Pn
(N)
PnT : carga aplicada (direções laterais)
g
: aceleração da gravidade
(m/s2)
(g =9,8m/s2)
V
: velocidade
(m/s)
: constante de tempo
(s)
tn
: aceleração
(m/s2)
n
V
(αn = tn
[Exemplo]
)
Condição
Equação de carga aplicada
Montagem horizontal
(com o percurso do bloco)
Movimento uniforme ou com paradas
P3
ℓ2
mg
P2 =
mg
mg•ℓ2
mg•ℓ3
–
–
2•ℓ0
2•ℓ1
4
P3 =
mg
mg•ℓ2
mg•ℓ3
–
+
2•ℓ0
2•ℓ1
4
P4 =
mg
mg•ℓ2
mg•ℓ3
+
+
2•ℓ0
2•ℓ1
4
P1 =
mg
mg•ℓ2
mg•ℓ3
+
+
2•ℓ0
2•ℓ1
4
P2 =
mg
mg•ℓ2
mg•ℓ3
–
+
2•ℓ0
2•ℓ1
4
P3 =
mg
mg•ℓ2
mg•ℓ3
–
–
2•ℓ0
2•ℓ1
4
P4 =
mg
mg•ℓ2
mg•ℓ3
+
–
2•ℓ0
2•ℓ1
4
ℓ1
P1
ℓ0
ℓ3
Montagem horizontal com balanço
(com o percurso do bloco)
Movimento uniforme ou com parada
P3
2
mg
mg•ℓ2
mg•ℓ3
+
–
4
2•ℓ0
2•ℓ1
P2
P4
1
P1 =
ℓ1
P2
P4
P1
ℓ0
ℓ3
mg
ℓ2
Nota) A carga é positiva na direção da seta.
B1-61
510BZ
Condição
Equação de carga aplicada
Montagem vertical
Movimento uniforme ou com parada
ℓ2
P4
P1T
3
P2 = P3 =
P1
ℓ0
mg•ℓ2
2•ℓ0
P1 = P4 = –
mg
mg•ℓ2
2•ℓ0
F
mg•ℓ3
2•ℓ0
P1T = P4T =
ℓ3
P2T = P3T = –
P2
P2T
mg•ℓ3
2•ℓ0
ℓ1
Por exemplo, eixo vertical de robô
industrial, máquina de revestimento
automático, elevador
Montagem na parede
Movimento uniforme ou com parada
ℓ0
P2T
ℓ3
ℓ2
P1T
P2
ℓ1
P1 = P2 = –
P3 = P4 =
P1
mg•ℓ3
2•ℓ1
4
P1T = P4T =
mg
mg•ℓ2
+
4
2•ℓ0
P2T = P3T =
mg
mg•ℓ2
–
2•ℓ0
4
P3
P3T
mg
P4
P4T
Por exemplo, eixo de percurso
de carregador de trilho cruzado
Nota) A carga é positiva na direção da seta.
B1-62
mg•ℓ3
2•ℓ1
510BZ
Diagrama de seleção
Cálculo da carga aplicada
Condição
Equação de carga aplicada
Com trilhos móveis
Montagem horizontal
P3
P1
5
P4
P1 a P4 (max) =
mg
mg•ℓ1
+
4
2•ℓ0
P1 a P4 (min) =
mg
–
4
ℓ0
Guia Linear
ℓ1
–ℓ1
P2
mg
mg•ℓ1
2•ℓ0
ℓ2
Por exemplo, mesa XY
Garfo deslizante
Montagem inclinada lateralmente
P1 = +
–
P1T=
P2 = +
–
P1
P3
P2T=
6
P2
ℓ3
ℓ1 θ
P2T
P3 = +
ℓ0
+
P3T=
+
P4T=
mg•cosθ •ℓ3
mg•sinθ •h1
+
2•ℓ1
2•ℓ1
mg•cosθ
mg•cosθ •ℓ2
–
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
–
2•ℓ1
2•ℓ1
mg•sinθ
mg•sinθ •ℓ2
–
2•ℓ0
4
P4 = +
Por exemplo, torno CN
Carro
mg•cosθ
mg•cosθ •ℓ2
–
2•ℓ0
4
mg•sinθ
mg•sinθ •ℓ2
–
2•ℓ0
4
P1T
ℓ2
mg•cosθ •ℓ3
mg•sinθ•h1
+
2•ℓ1
2•ℓ1
mg•sinθ
mg•sinθ •ℓ2
+
2•ℓ0
4
h1
mg
mg•cosθ
mg•cosθ •ℓ2
+
2•ℓ0
4
mg•cosθ
mg•cosθ •ℓ2
+
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
–
2•ℓ1
2•ℓ1
mg•sinθ
mg•sinθ •ℓ2
+
2•ℓ0
4
Nota) A carga é positiva na direção da seta.
B1-63
510BZ
Condição
Equação de carga aplicada
Montagem inclinada longitudinalmente
P1 = +
–
P1T = +
P3
h1
P2 = +
P2
mg
P2T
–
P4
ℓ2
P1
7
P1T
ℓ3
ℓ1
mg•cosθ
mg•cosθ •ℓ2
+
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
+
2•ℓ1
2•ℓ0
mg•sinθ •ℓ3
2•ℓ0
mg•cosθ
mg•cosθ •ℓ2
–
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
–
2•ℓ1
2•ℓ0
mg•sinθ •ℓ3
2•ℓ0
P2T = –
ℓ0
θ
P3 = +
+
mg•cosθ
mg•cosθ •ℓ2
–
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
–
2•ℓ1
2•ℓ0
mg•sinθ •ℓ3
2•ℓ0
P3T = –
P4 = +
Por exemplo, torno CN
Descanso de ferramenta
+
P4T = +
Montagem horizontal com inércia
mg
mg•cosθ
mg•cosθ •ℓ2
+
2•ℓ0
4
mg•cosθ •ℓ3
mg•sinθ •h1
+
2•ℓ1
2•ℓ0
mg•sinθ •ℓ3
2•ℓ0
Durante a aceleração
P1 = P4 =
mg
–
4
m•α 1•ℓ2
2•ℓ0
P2 = P3 =
mg
+
4
m•α 1•ℓ2
2•ℓ0
P1T = P4T =
ℓ3
P1
ℓ2
P2T = P3T = –
P3
P4
P3T
ℓ0
Velocidade V (m/s)
ℓ1
P4T
t1
t2
t3 Tempo (s)
Diagrama da velocidade Por exemplo, caminhão
de transporte
B1-64
P1 a P4 =
mg
4
Durante desaceleração
V
αn =
tn
Nota) A carga é positiva na direção da seta.
m•α 1•ℓ3
2•ℓ0
Durante movimento uniforme
8
F
m•α 1•ℓ3
2•ℓ0
P1 = P4 =
mg
+
4
m•α 3•ℓ2
2•ℓ0
P2 = P3 =
mg
–
4
m•α 3•ℓ2
2•ℓ0
P1T = P4T = –
P2T = P3T =
m•α 3•ℓ3
2•ℓ0
m•α 3•ℓ3
2•ℓ0
510BZ
Diagrama de seleção
Cálculo da carga aplicada
Condição
Montagem vertical
com inércia
Equação de carga aplicada
P4
mg
P1T
ℓ0
P1
F
ℓ3
P2
αn =
P2T
9
V
tn
Velocidade V (m/s)
ℓ1
t1
t2
t3 Tempo (s)
Diagrama da velocidade
Por exemplo, elevador
de transporte
Montagem horizontal com
força externa
F1
10
F
F1•ℓ5
2•ℓ0
F1•ℓ5
P2 = P3 =
2•ℓ0
F1•ℓ4
P1T = P4T =
2•ℓ0
F1•ℓ4
P2T = P3T = –
2•ℓ0
P3
ℓ1
F3
P3T
P4
P4T
ℓ3
Durante desaceleração
m (g – α 3) ℓ2
P1 = P4 = –
2•ℓ0
m (g – α 3) ℓ2
P2 = P3 =
2•ℓ0
m (g – α 3) ℓ3
P1T = P4T =
2•ℓ0
m (g – α 3) ℓ3
P2T = P3T = –
2•ℓ0
Sob força F1
ℓ4
ℓ5
Durante movimento uniforme
mg•ℓ2
P1 = P4 = –
2•ℓ0
mg•ℓ2
P2 = P3 =
2•ℓ0
mg•ℓ3
P1T = P4T =
2•ℓ0
mg•ℓ3
P2T = P3T = –
2•ℓ0
P1 = P4 = –
ℓ2
F2
Guia Linear
Durante a aceleração
m (g+α 1) ℓ2
P1 = P4 = –
2•ℓ0
m (g+α 1) ℓ2
P2 = P3 =
2•ℓ0
m (g+α 1) ℓ3
P1T = P4T =
2•ℓ0
m (g+α 1) ℓ3
P2T = P3T = –
2•ℓ0
ℓ2
ℓ0
Por exemplo, furadeira,
fresadora,
torno,
centro de usinagem
e outras máquinas de corte
Sob força F2
F2
+
4
F2
–
P2 = P3 =
4
P1 = P4 =
F2•ℓ2
2•ℓ0
F2•ℓ2
2•ℓ0
Sob força F3
F3•ℓ3
2•ℓ1
F3•ℓ3
P3 = P4 = –
2•ℓ1
F3
P1T = P4T = –
–
4
F3
+
P2T = P3T = –
4
P1 = P2 =
F3•ℓ2
2•ℓ0
F3•ℓ2
2•ℓ0
Nota) A carga é positiva na direção da seta.
B1-65