GEOMETRIA: QUINTA LISTA DE EXERCÍCIOS

GEOMETRIA: QUINTA LISTA DE EXERCÍCIOS
UMA FIGURA AJUDA OU ATRAPALHA?
[01] A seguir temos cinco passos de uma demonstração errada para o seguinte teorema falso: “todo triângulo é
isósceles'”. Quais passos estão errados? Quais passos estão corretos? Separem-se em três grupos: o primeiro grupo
tentará responder a estas perguntas só com o enunciado (cabe aos alunos deste grupo decidirem se farão ou não uso de
uma figura por eles desenhados com lápis, régua e compasso); o segundo grupo tentará respondê-las com uma figura
fornecida pelo professor; o terceiro grupo fará a atividade construindo a figura usando o GeoGebra.
PASSO 1. No triângulo ∆ABC, seja O o ponto de interseção da mediatriz FO do lado AB com a bissetriz CO do
ângulo ACB.
PASSO 2. Construa os segmentos OE perpendicular ao lado AC e DO perpendicular ao lado BC, respectivamente.
PASSO 3. Os triângulos retângulos ∆CEO e ∆CDO são congruentes e, portanto, EO = DO e EC = DC.
PASSO 4. Como AO = BO, o triângulo retângulo ∆AEO é então congruente ao triângulo retângulo ∆BDO e, assim,
AE = BD.
PASSO 5. Consequentemente, AC = AE + EC = BD + DC = BC e o triângulo ∆ABC é isósceles.
As três atividades seguintes também serão realizadas por três grupos: o primeiro grupo tentará responder a estas
perguntas só com o enunciado (cabe aos alunos deste grupo decidirem se farão ou não uso de uma figura por eles
desenhados com lápis, régua e compasso); o segundo grupo tentará respondê-las com uma figura fornecida pelo
professor; o terceiro grupo fará a atividade construindo a figura usando o GeoGebra.
[02] (Dvora e Dreyfus, 2004) Considere um paralelogramo ABCD. Seja F o ponto de interseção da bissetriz do ângulo
BCD com a reta AB e seja E o ponto de interseção dessa bissetriz com a bissetriz do ângulo ABC. Mostre que FE
= EC.
[03] (Dvora e Dreyfus, 2004) Seja ABC um triângulo isósceles com AC = AB. Sejam D e E pontos sobre a reta BC de
tal modo que B está entre D e C, C está entre B e E e DAB = CAE , Mostre que DB = CE.
[04] (Dvora e Dreyfus, 2004) Considere um paralelogramo ABCD. Seja F o ponto médio do lado DC e seja E o ponto
interseção das retas AD e BF. Mostre que AD = DE.
1
Figura da Atividade [01]
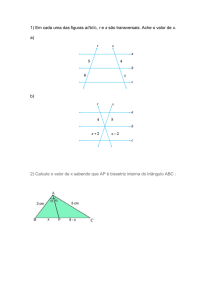
Figura da Atividade [02]
Figura da Atividade [03]
Figura da Atividade [04]
2