Notas de aula

HEP-5800 – BIOESTATÍSTICA
Capitulo 2
NOÇÕES DE PROBABILIDADE, DISTRIBUIÇÃO BINOMIAL,
DISTRIBUIÇÃO NORMAL
Nilza Nunes da Silva
Regina T. I. Bernal
MARÇO DE 2012
2
1. NOÇÕES DE PROBABILIDADE
1. DEFINIÇÃO
Considere o lançamento de um dado uma única vez e imagine o
CONJUNTO DE TODOS POSSIVEIS RESULTADOS
S = {1, 2 , 3, 4, 5, 6}
Esse conjunto é formado por seis eventos simples, mutuamente exclusivos, e igualmente
prováveis . Chama-se ESPAÇO AMOSTRAL .
Portanto P(1)=P(2)=P(3)=P(4)=P(5)=P(6)= 1/6
E a probabilidade de ocorrer um evento favorável é definida pela expressão :
Então , a probabilidade de ocorrer números pares será igual a P(A) = 3/6
Definição operacional encontrada no livro Introdução à Bioestatística (Sonia Vieira, pág.71) .......
Se são possíveis n eventos mutuamente exclusivos e igualmente prováveis, e se m desses eventos
têm determinada característica, a probabilidade de que ocorra um evento com essa característica é
dada pela razão ( m/n ) .
Então, numa seqüência de 1000 partos observados em determinado período, a probabilidade de
ocorrência de parto normal pode ser calculada usando a definição acima :
TIPO DE PARTO
N = 1000
PROB (PARTO SER NORMAL) = 100 / 1000
(900)
CESAREO
(100)
NORMAL
3
2. PROPRIEDADES
1. PROBABILIDADE DE QUALQUER EVENTO é um número entre zero e um
0 <=P ( E ) =< 1
2. P ( 1 ) = 0
3.P ( 0 ) = 0
4. Soma das probabilidades dos eventos simples é igual a 1 .
3. EVENTOS COMPOSTOS
Uma moeda é lançada 3 vezes . Qual a probabilidade de ocorrer o resultado ( cara,
cara, coroa) ? Ou seja, o evento = duas caras .
Espaço amostral é composto pelos eventos simples:
S = { (ca,ca,ca) (ca,ca,co) (ca,co,ca) (co,ca,ca) (ca,co,co) (co,ca,co) (co,co,ca) (
co,co,co )}
Mas , um evento pode ser formado pela união dos eventos simples, como OCORRER
DUAS CARAS pode ser expresso pelo conjunto formado reunindo o segundo, com
o terceiro e o quarto eventos simples.
P(ocorrer duas caras e uma coroa ) = 1/8 + 1/8 + 1/8 = 3/8 .
Então : usando o espaço amostral, será definida a seguinte distribuição de probabilidades
P(X=K)
K
P( X )
0
1/8
1
3/8
2
3/8
3
1/8
SOMA
8/8=1
4
4. DISTRIBUIÇÕES TEÓRICAS
São modelos teóricos que possuem parâmetros e permitem calcular as probabilidades de eventos
simples ou compostos . Os valores das probabilidades encontram-se em tabelas que podem ser
facilmente utilizadas.
VARIAVEIS DISCRETAS
X = numero de sucessos
BERNOULLI
(n=1)
S= {0,1}.
e as probabilidades correspondentes aos eventos
são definidas por P(X=1) = p ; P(X=0) = (1-p) = q
MÉDIA = p Variância = (p . q )
Se n => 2
..............................DISTRIBUIÇÃO BINOMIAL
1) São realizadas (n) observações independentes
2) cada resultado DE UMA OBSERVAÇÃO é dicotômico ( SIM ou NÃO)
3) em cada resultado, a probabilidade de ocorrer SIM é igual a (p) ; e a de ocorrer NÃO é
igual (1-p) ou (q) .
4) p+q=1
X : número de elementos com resultado ( SIM )
.n=2
Espaço amostral (S)
EVENTOS DE S
X=
PRODUTO DE
PROBABILIDADE
EVENTOS
INDEPENDENTES
0
(0,0)
0,3 x 0,3
0,09
1
(1,0)ou(0,1)
2(0,7 x 0,3)
0,42
2
(1,1)
0,7 x 0,7
0,49
SOMA
1,00
5
.n=3
Espaço amostral (S)
EVENTOS DE S
PRODUTO
PROBABILIDADE
0
(0,0,0)
0,3X0,3X0,3
0,33=0,027
1
(1,0,0)ou(0,1,0)ou(0,0,1)
3(0,7X0,32)
0,189
2
(1,1,0)ou(1,0,1)ou(0,1,1)
3(0,72x0,3)
0,441
3
(1,1,1)
0,7x0,70,7
0,343
SOMA
1,000
.n=4
Esp.amostral
EVENTOS DE S
PRODUTO PROBABILIDADE
(S)
0
(0,0,0,0)
0,34
0,0081
1
(1,0,0,0)ou(0,1,0,0)ou(0,0,1,0),(0,0,0,1)
4(0,7X0,33)
0,0756
2
(1,1,0,0)ou(1,0,1,0)ou(1,0,0,1)ou
6(0,72x0,32)
0,2646
(0,1,1,0)ou(0,1,0,1)ou(0,0,1,1)
3
(1,1,1,0)ou(1,1,0,1)ou(1,0,1,1)ou(0,1,1,1)
4(0,73x0,3)
0,4116
4
(1,1,1,1)
0,74
0,2401
SOMA
Observe agora a expressão que calcula P(X=1) =
1,0000
4 (0,7 )1 (0,33)
4 expressa o número de eventos que resultam em 4 diferentes combinações de 1 (SIM) E 3 (NÃO) .
p(X = 1 ) = C4,1 ( p1 ) ( q3 )
PODEMOS ENTÃO CONTINUAR DEFININDO AS DEMAIS EXPRESSÕES....
P(X = 2) = C4,2 x p2 x q2
P(X = 3) = C4,3 x p3 x q1
P(X = 4) = C4,4 x p4 x q0
6
Então, a distribuição de probabilidades de X, pode ser expressa pela equação .......
P(X = k) = Cn,k x pk x q n -k
que é o modelo da distribuição BINOMIAL COM PARÂMETROS (n)
e (p) .
MÉDIA = (n . p) Variância = (n . p . q )
Cn,k
= expressa o número de eventos que resultam em k diferentes combinações de k (SIM) E ( n
– k ) (NÃO) . Fatorial de um número é calculado como abaixo
n! / k! ( n – k ) ! .n ! = n ( n-1) (n-2).....(1) .
CONCLUSAO : Se X é uma variável aleatória que expressa o numero de
sucessos dentro das seguintes condições:
1 ) São realizadas (n) observações independentes
2) Cada resultado DE UMA OBSERVAÇÃO é dicotômico ( SIM ou NÃO)
3) em cada resultado, a probabilidade de ocorrer SIM é igual a (p) ; e a de ocorrer NÃO é
igual (1-p) ou (q) .
4) p+q=1
A DISTRIBUIÇÃO DE PROBABILIDADE DE (X) é expressa pelo
modelo binominal com parâmetros (n) e (p) . Ou seja, X : B(n, p) .
A média de X é
= (n . p ) e seu desvio padrão
2
=(n.p.q)
7
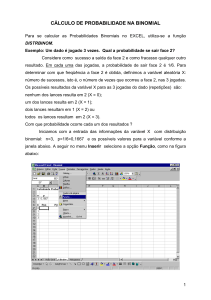
5. Usando a tabela Binomial (n,p)
Os valores da expressão da binomial encontram-se tabelados. Podemos encontrar as probabilidades
correspondentes aos valores de (X), dados os valores de (n) e (p).
Em 5 nascimentos, se X : Número de nascituros do sexo masculino
.n = 5
X
.p=0,10
.p=0,4
.p=0,50
0
0,59049
0,07776
0,03125
1
0,32805
0,25920
0,15625
2
0,07290
0,34560
0,31250
3
0,00810
0,23040
0,31250
4
0,00045
0,07680
0,15625
5
0,00001
0,01024
0,03125
.p=0,6
0,01024
0,07680
0,23040
0,34560
0,25920
0,07776
A ) Probabilidade de nascerem 3 crianças do sexo masculino se n=5 e p = 0,6 ........0,34560
B ) Probabilidade de nascerem 2 crianças do sexo masculino se n=5 e p = 0,4 .........0,34560
Observe nas expressões abaixos porque as probabilidades são iguais...................
P(X = 3) = C5,3 . 0,63 . 0,42
P(X = 2) = C5,2 . 0,42 . 0,63
8
Exercícios:
1) Analisando prontuários de várias maternidades, estimou-se que a probabilidade de um
parto ser cesariano é de 10%. Em 7 partos de uma maternidade qualquer:
a) Defina a variável aleatória a ser observada e o respectivo espaço amostral .
b) Defina a expressão matemática que calcula a distribuição de probabilidade dessa variável.
c) Apresente a tabela com a distribuição de probabilidades.
d) Calcule a probabilidade de 5 partos serem cesarianos.
e) A probabilidade de que todos os partos serem normais.
f) A probabilidade de que no máximo haja 1 parto cesariano.
2) Apresente em tabela e gráfico a distribuição de número de meninos que pode ocorrer em uma
família com 6 crianças.
3) Suponha que determinado medicamento usado para diagnóstico precoce da gravidez é capaz de
confirmar casos positivos em apenas 90% das gestantes muito jovens. Nestas condições, qual é a
probabilidade de duas entre três gestantes muito jovens, que fizeram uso desse medicamento, não
terem confirmado precocemente a gravidez.
4) Seja X a variável aleatória que indica o número de meninos em uma família com 5 crianças.
Apresente a distribuição de X em uma tabela, considerando a probabilidade de menino igual a
1
e
2
1
.
3
5) Um exame é constituído de dez testes tipo certo-errado. Quantos testes acerta, em média, um
aluno que nada sabe sobre a matéria do exame? Qual é a variância
da distribuição?
6 - A probabilidade de um animal sobreviver durante um experimento é 2/3. Seja X o número de
animais que sobrevivem ao experimento.
a) – Se 5 animais forem submetidos ao experimento, determine a distribuição de probabilidade de
X.
b) – Determine a probabilidade de:
-
exatamente 3 animais sobreviverem
os 5 animais não sobreviverem
pelo menos 3 animais sobreviverem
7 – A probabilidade de um menino ser daltônico é 0,08. Num grupo de 4 meninos , qual a
probabilidade de 3 não serem daltônicos?
9
8) Entre 800 famílias com 5 crianças cada uma, quantas se esperaria que tivessem:
a) Três meninos
b) cinco meninas
c) dois ou três meninos
Considerar probabilidades iguais para meninos e meninas.
9) Pesquisa médica indica que 20% da população em geral sofrem efeitos colaterais negativos com
o uso de uma nova droga. Se um médico receita o produto a três, qual a probabilidade de:
a)
b)
c)
d)
e)
nenhum sofre efeito colateral negativo?
um sofrer efeito colateral negativo?
dois sofrerem efeito colateral negativo?
três sofrerem efeito colateral negativo?
ao menos um sofrer efeito colateral negativo?
10) Pesquisas indicaram que 75% dos eleitores de uma cidade são alfabetizados. Entre 16 eleitores
dessa cidade, determine a probabilidade de:
a)
b)
c)
d)
no máximo um ser analfabeto
dois ou mais serem analfabetos
três ou mais serem analfabetos
pelo menos um ser analfabeto
11) Se a probabilidade de um indivíduo ter sangue Rh é 5%, qual é a probabilidade de 10
indivíduos que se apresentaram para exame de sangue:
a) todos terem Rh ?
b) No máximo dois indivíduos apresentarem Rh ?
10
DISTRIBUIÇÃO NORMAL
APRESENTAÇÃO
+
-
x
CARACTERÍSTICAS:
A)
A variável pode assumir qualquer valor no conjunto real.
B)
O gráfico da distribuição é uma curva em forma de sino, simétrica em torno da média
, que é igual à mediana e à moda.
C)
A área sob a curva é igual a 1, e corresponde à probabilidade de a variável assumir
valores entre [
].
......
;
D)
(Mi e Sigma) representam os parâmetros de posição e dispersão da
distribuição.
E)
Os pontos de inflexão da curva ocorrem nos valores definidos por (
).
F)
A expressão da função densidade de probabilidade é:
f (X )
1
.e
2
1 / 2[(
) / ]2
e
11
Na figura abaixo, 68,28% é a probabilidade de valores ocorrerem para X entre a média e mais ou
menos 1 desvio padrão.
Ou seja:
P [(
) < X <(
)] = 68,28%
Também
P [(
2
) < X <(
2
)] = 95, 44%
µ
P [(
3
) < X <(
µ
x
3
)] = 99,74%
x
12
NORMAL PADRONIZADA: Z~N(0;1)
-3
-2
-1
1
2
3
Se X tem distribuição normal, então:
Z
tem distribuição normal com média igual a zero e desvio padrão igual a 1.
Ou seja, Z ~ N (0 , 1) . Os valores das probabilidades associadas a esta distribuição encontram-se
em tabelas. Veja abaixo um trecho dessa tabela, e aprenda como localizar os valores para as
probabilidades de ocorrência de Z entre zero e z.
Ou seja, P[0 <Z < z].
P(0 < Z <z) Probabilidades de ocorrer valores entre 0 e z.
Valores de z
com
Uma decimal
Segunda decimal
0
1
2
3
4
5
6
0,0
0,1
0,2
0,3
0,4
0,5
1,0
1,2
0,0000
0,0398
0,0793
0,1179
0,1554
0,1915
0,3413
0,3849
0,0040
0,0438
0,0832
0,1217
0,1591
0,1950
0,3438
0,3869
0,0080
0,0478
0,0871
0,1255
0,1628
0,1985
0,3461
0,3888
0,0120
0,0517
0,0910
0,1293
0,1664
0,2019
0,3485
0,3907
0,0160
0,0557
0,0948
0,1331
0,1700
0,2054
0,3508
0,3925
0,0199
0,0596
0,0987
0,1368
0,1736
0,2088
0,3531
0,3944
0,0239
0,0636
0,1026
0,1406
0,1772
0,2123
0,3554
0,3962
Fonte: Introdução à Bioestatística. Sonia Vieira, pág.92
Então, a probabilidade de ocorrer valores para z entre 0 e 1 é igual a 0,3413. Ou a probabilidade
de ocorrer valores para Z maiores que 1 é igual a 0,50 – 0,3413 = 0,1587.
13
Exemplos:
I - Suponha que a quantidade de colesterol em 100 ml de plasma sanguíneo humano tem
distribuição normal com média 200 mg e desvio padrão 20 mg.
1) Qual a probabilidade de uma pessoa apresentar entre 200 e 225 mg de colesterol por 100 ml
de plasma ?
X ~N (200 mg ; 20 mg) ……..Z ~ (0 ; 1)
Z1
200 200
20
0
Z2
225 200
1,25
20
P (0< Z <1,25) = 0,3944
2 ) Qual a probabilidade de uma pessoa apresentar menos do que 190 mg de colesterol por 100
ml de plasma ?
Z
190 200
20
0,50
P ( X < 190) = P (Z < -0,50 ) = 0,50 – P (0 < Z < -0,50)
= 0,50 – 0,1915
= 0,3085
3) Qual a probabilidade de uma pessoa apresentar mais do que190 mg de colesterol por 100 ml
de plasma?
P ( X > 190) = P(Z > -0,50) = 0,50 + 0,1915 = 0,6915
II – Em homens, a quantidade de hemoglobina por 100ml de sangue é uma variável aleatória com
distribuição normal de média igual a 16 gr e desvio padrão igual a 1 gr.
1) Calcule a probabilidade de um homem apresentar de 16 a 18 gr de hemoglobina por 100 ml de
sangue.
Então X = quantidade de hemoglobina por 100 ml de sangue.
X ~ N(16 , 1 )
P ( 16 < X < 18 ) = P ( 0 < Z < 2 ) = 0,4772 ou 47,72% .

consulte a tabela Z
2) Qual é a probabilidade de um homem apresentar mais de 18 gr de hemoglobina por 100ml de
sangue?
P ( X > 18 ) = P ( Z > 2 ) = 0,50 – 0,4772 = 0,0228 ou 2,28 %.
14
4. APROXIMAÇÃO DA BINOMIAL PARA NORMAL
Seja X o número de meninos em 16 nascituros, onde X ~ B(16, ½). Essa variável pode assumir
qualquer valor inteiro entre zero e 16, inclusive. A distribuição dessa variável é dada por:
Número de meninos (X)
P(X=x)
0
0,00153
1
0,02441
2
0,18311
3
0,85449
4
2,77710
5
6,66504
6
12,21924
7
17,45605
8
19,63806
9
17,45605
10
12,21924
11
6,66504
12
2,77710
13
0,85449
14
0,18311
15
0,02441
16
0,00153
Por exemplo: Calcular a probabilidade de serem do sexo masculino mais de 10 recém-nascidos
que estão no berçário de um determinado hospital:
P(X > 10) = P(X=11) + P(X=12) + P(X=13) + P(X=14) + P(X=15) + P(X=16)
= 0,1050568 ou 10,50568%
15
Gráfico da distribuição do número de meninos em 16 nascituros
20
15
10
5
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16
Número de meninos
Aproximação da binomial para normal é adequada quando:
np> 5 e nq > 5
No exemplo:
np 16.
1
2
8 5
nq 16.
1
2
8 5
e
A condição para aproximação da distribuição binomial para a distribuição normal é satisfeita, logo:

X ~ B(16,1/2)
np 16.
npq
X ~ N(8,2)
1
2
8
1 1
16 . .
2 2
2
16
Gráfico da distribuição normal
20
15
10
5
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16
Número de meninos
A distribuição normal é contínua e pode assumir qualquer valor real. Portanto, para calcular a
probabilidade de serem do sexo masculino mais de 10 recém-nascidos será necessária uma
correção da continuidade em função da passagem da distribuição discreta para uma contínua.
Correção da continuidade
Binomial: P(X=x)
Normal: P(X= x – 0,5) a P(X = x + 0,5)
Exemplo:
Distribuição Binomial
X ~ B(16,1/2)
P(X> 10) ?
Distribuição Normal
X ~ N(8,2)
x
-----|-------|------|
10
11 12
P(X > 11- 0,5)=?
z
P(X > 10) = 0,1051 –ou 10,51%
10,5 8
2
1,25
P(Z > 1,25) = 0,50 – 0,3944 = 0,1056 ou 10,56%
0,1056
zc=1,25
17
INTERVALO DE REFERÊNCIA
USANDO A DISTRIBUIÇÃO NORMAL
Testes de diagnósticos em medicina clínica são usados para classificar a situação de saúde dos
indivíduos. Servem para definir se o estado de saúde pode ser considerado dentro de um padrão
aceitável, e elaborar o diagnóstico.
Esse padrão é estabelecido mediante o uso de distribuições de probabilidade das características
observadas em grande número de indivíduos considerados sadios. As medidas de posição e de
variabilidade dessas distribuições serão os parâmetros utilizados para construir os intervalos de
referência com os quais são avaliadas as mais variadas características dos seres vivos.
A tabela 3.1 apresenta intervalos de referência para o pH observado no couro cabeludo de fetos
observados em 14 diferentes conjuntos de mulheres observadas em diferentes hospitais. Supondo
que pH tem distribuição normal, calculou-se em cada conjunto os limites dos intervalos que
2 ). Nota-se que o numero
contem 95% dos indivíduos. Ou seja, os pontos definidos por ( X
de mulheres em cada conjunto não altera a amplitude dos intervalos para essa característica.
Tabela 3.1
Intervalos de referência para 14 estudos de pH sangue couro cabeludo em fetos.
ESTUDO
Ph MÉDIO
IR (95%)*
N
1
7,29
7,15 ― 7,43
43
2
7,29
7,21 ― 7,37
24
3
7,29
7,25 ― 7,33
10
4
7,30
7,20 ― 7,40
12
5
7,30
7,22 ― 7,38
18
6
7,30
7,22 ― 7,38
129
7
7,32
7,20 ― 7,44
16
8
7,32
7,22 ― 7,42
49
9
7,35
7,23 ― 7,47
45
10
7,35
7,25 ― 7,45
26
11
7,35
7,25 ― 7,45
29
12
7,35
7,25 ― 7,45
21
13
7,37
7,27 ― 7,47
45
14
7,38
7,30 ― 7,45
22
Fonte : Altman GD . Practical Statistics for Medical Research, pag. 422.
Média mais ou menos 2 desvios padrão. Ou seja, ( X
2
)
18
EXERCICIOS
A) Seja Z ~ N (0,1). Calcule:
a) P(0 <Z< 1,2)
b) P(-0,9 Z 0)
c) P(1,21 Z 1,75)
d) (Z > -0,75)
e) (Z < 1,35)
f) P(-1,44 < Z < 0)
g) P(-1,96 < Z < 1.96)
B) Suponha que o tempo médio de permanência em um hospital para doenças crônicas sejam
50 dias, com desvio padrão igual a 10 dias . Admitindo que o tempo de permanência tem
distribuição normal, qual é a probabilidade de uma paciente permanecer no hospital:
a) mais de 30 dias ?
b) menos de 30 dias ?
c) mais de 50 dias ?
d) entre 40 e 60 dias ?
e) entre 30 e 70 dias ?
C) A idade de uma população tem distribuição normal com média 50 anos e desvio padrão de 4
anos. Qual a probabilidade de uma pessoa dessa população ter:
a) 55 anos ou menos?
b) exatamente 50 anos?
c) mais de 55 anos?
d) entre 55 e 57 anos?
e) entre 42 e 50 anos?
f) idade entre a média e mais ou menos 1 desvio padrão?
g) idade entre a média e mais ou menos 2desvios padrão?
h) idade entre a média e mais ou menos 3 desvios padrão?
D) Numa curva normal reduzida, a área compreendida entre –1,64 e zero vale 45%. Nestas
condições a área à direita do valor +1,64 valerá:
a) 45%
b) infinito
c) 50%
d) 100%
e) 5%