Se dois triângulos possuem os lados homólogos proporcionais

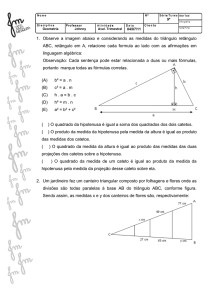
3º caso- Se dois triângulos possuem os lados homólogos proporcionais, então, esses
triângulos são semelhantes.
Polígonos semelhantes- Dois polígonos convexos são semelhantes se os ângulos de um
deles são ordenadamente congruentes aos ângulos do outro e se os seus lados
homólogos são proporcionais.
Se os polígonos ABCD e A’B’C’D’ forem semelhantes, então, teremos:
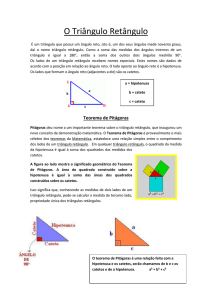
Relações Métricas no
triângulo retângulo
Elementos de um triângulo retângulo
a é a medida da hipotenusa
b e c são as medidas dos catetos
m e n são as medidas das projeções dos catetos sobre a
hipotenusa. Observe que m+n=a
Relações métricas no triângulo retângulo
1- bc= ah, isto é, o produto dos catetos é igual ao produto da hipotenusa pela altura a ela
relativa..
2 e 3- b2 = am, isto é, o quadrado de qualquer um dos catetos é igual ao produto da
hipotenusa pela projeção do cateto considerado sobre a hipotenusa.
4- h2 = mn, isto é, a altura relativa à hipotenusa é igual ao produto das projeções dos
catetos sobre a hipotenusa.
5- a2= b2+c2, isto é, o quadrado da hipotenusa é igual à soma dos quadrados dos
catetos.(Teorema de Pitágoras)
Aplicações do Teorema de Pitágoras
1) A medida da diagonal de um quadrado cujo lado mede l.
d = l√2
2) A medida da diagonal de um cubo cuja aresta mede l.
d = l√3
3) A altura de um triângulo equilátero cujo lado mede l.
h = l√3
2
Relações métricas na
circunferência
-
A relação entre as medidas de duas cordas que se interceptam
PA . PB = PC. PD
-
A relação entre as medidas de duas secantes traçadas de um mesmo ponto
PA . PB = PC. PD
-
A relação entre as medidas de uma secante e de uma tangente traçadas de um
mesmo ponto.
PC2 = PA . PB