PE DE MATEMÁTICA WORD

MÓDULOS: 3 - Números racionais, Produtos notáveis (II), Equação do 2° grau, Desigualdades, Relações métricas
no triângulo retângulo.
4 - Sistema de numeração, Racionalização, Equação biquadrada, Polígonos, Trigonometria básica.
01. Se a denota um número irracional e r um número
racional não nulo, classifique como verdadeira (V) ou falsa
(F) cada uma das afirmações a seguir, para quaisquer a e r,
nas condições enunciadas.
a) r.a é um número irracional ( )
b) r/a é um número racional ( )
c) a/r é um número irracional ( )
d) a + r é um número racional( )
e) a – r é um número irracional ( )
A) 18,8 m. B) 19,2 m. C) 19,6 m. D) 20,0 m. E) 20,4 m.
2
 a +1
02. 
 representa o mesmo que:
 a −1
A)
a 2 + 2a + 1
a −1
B)
D)
a +1
2
a − 2a + 1
E)
a2 −1
C)
2
a +1
a2 +1
a2 −1
A) 8
a 2 + 2a + 1
a 2 − 2a + 1
03. Certa pessoa escrevendo a sucessão dos números
inteiros positivos, interrompeu seu trabalho em certo
número. Em que número parou, se, até este número, tinha
empregado 1.506 algarismos?
A) 358
B) 385
C) 538
D) 583
E) 590
04. O número de diagonais de um polígono é o sêxtuplo do
número de lados. Calcular a soma dos ângulos internos
desse polígono.
A) 1080°
B) 2520°
C) 2340°
D) 720°
2
E) 660°
2
05. Para que valores de K reais, a equação (K − 4) x + 2x = 0 é
uma equação do 2º grau.
A) K = ± 2
B) K ≠ ± 2
C) K = 2
D) K = − 2
E) K ≠ 2
06. Em um triângulo retângulo, o quadrado da hipotenusa é
o dobro do produto dos catetos. Calcular um dos ângulos
agudos do triângulo.
A) 30°
B) 60°
C) 45°
08. Em um triângulo retângulo onde a altura relativa à
hipotenusa mede 4,8 e um dos seus catetos mede 6, terá
hipotenusa igual a:
D) 27°
E) 15°
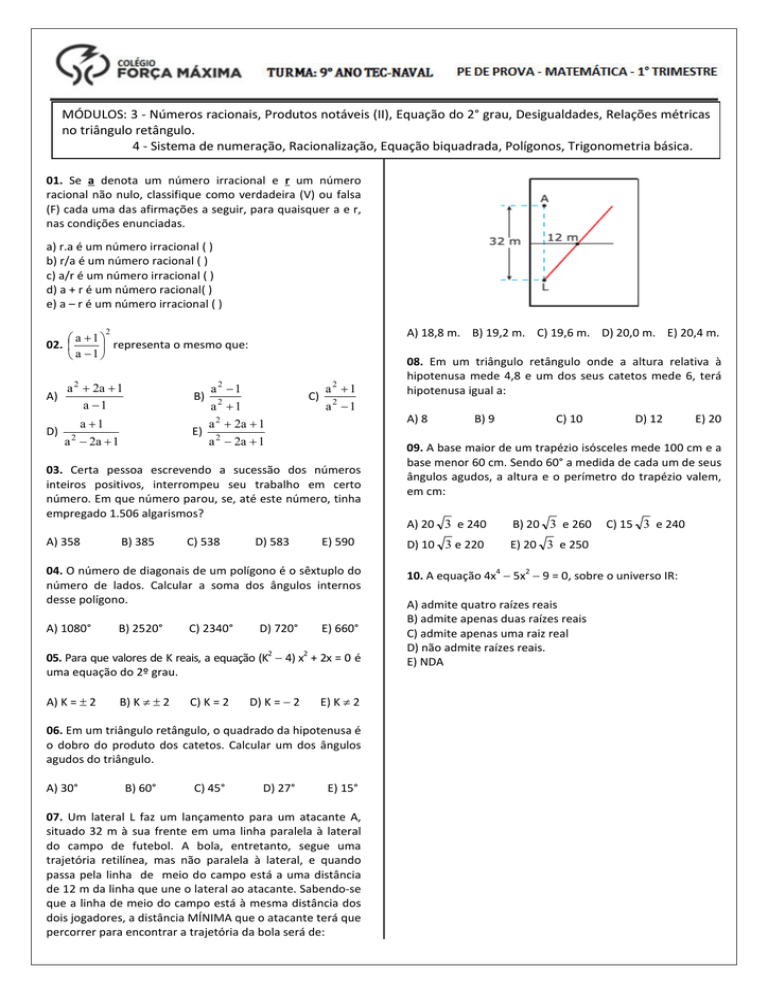
07. Um lateral L faz um lançamento para um atacante A,
situado 32 m à sua frente em uma linha paralela à lateral
do campo de futebol. A bola, entretanto, segue uma
trajetória retilínea, mas não paralela à lateral, e quando
passa pela linha de meio do campo está a uma distância
de 12 m da linha que une o lateral ao atacante. Sabendo-se
que a linha de meio do campo está à mesma distância dos
dois jogadores, a distância MÍNIMA que o atacante terá que
percorrer para encontrar a trajetória da bola será de:
B) 9
C) 10
D) 12
E) 20
09. A base maior de um trapézio isósceles mede 100 cm e a
base menor 60 cm. Sendo 60° a medida de cada um de seus
ângulos agudos, a altura e o perímetro do trapézio valem,
em cm:
A) 20 3 e 240
B) 20 3 e 260
D) 10 3 e 220
E) 20 3 e 250
4
2
C) 15 3 e 240
10. A equação 4x − 5x − 9 = 0, sobre o universo IR:
A) admite quatro raízes reais
B) admite apenas duas raízes reais
C) admite apenas uma raiz real
D) não admite raízes reais.
E) NDA