Apresentação do PowerPoint

25/10/2016
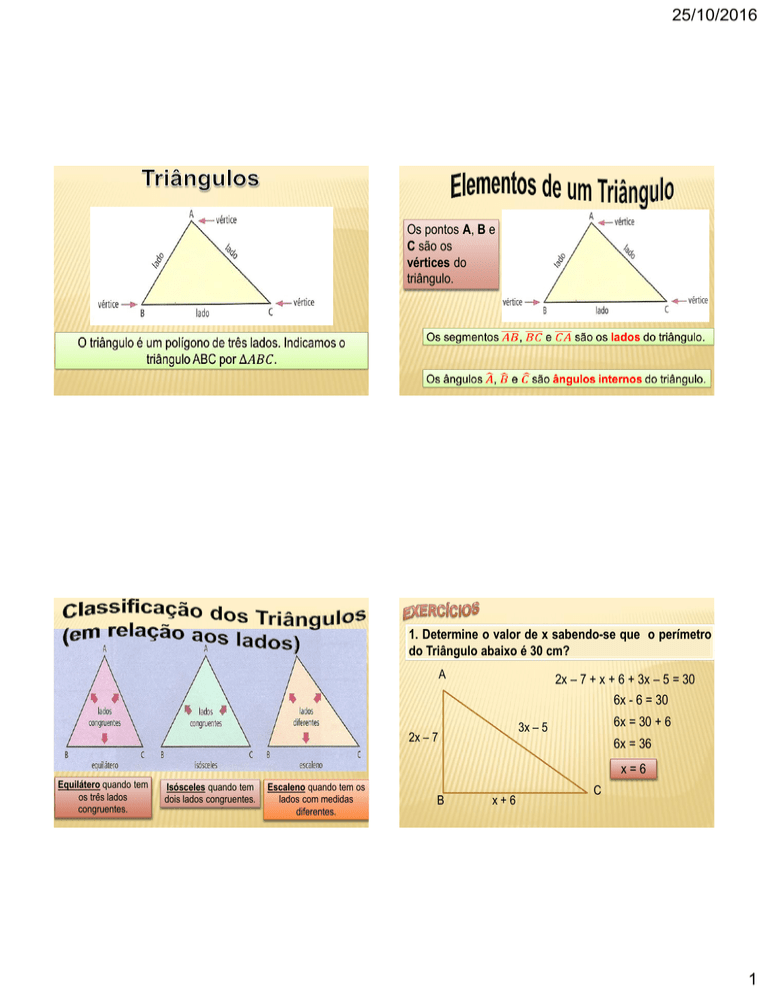
Os pontos A, B e
C são os
vértices do
triângulo.
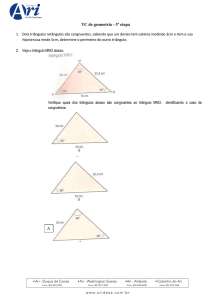
1. Determine o valor de x sabendo-se que o perímetro
do Triângulo abaixo é 30 cm?
A
2x – 7 + x + 6 + 3x – 5 = 30
6x - 6 = 30
6x = 30 + 6
3x – 5
2x – 7
6x = 36
x=6
Equilátero quando tem
os três lados
congruentes.
Isósceles quando tem
dois lados congruentes.
Escaleno quando tem os
lados com medidas
diferentes.
B
x+6
C
1
25/10/2016
5 cm
Acutângulo quando
tem os três ângulos
agudos.
Retângulo quando tem
um ângulo reto.
Obtusângulo quando tem
um ângulo obtuso.
Desigualdade triangular:
Num triângulo, o comprimento
de qualquer lado é menor que a
soma dos comprimentos dos
outros dois.
AB  5 cm ; BC  7 cm ; AC  4 cm
5  7  12  4
7  4  11  5
5 4  9  7
É possível construir o triângulo ABC.


med (â) + med ( b ) + med( c ) = 180°
2
25/10/2016


med (Â) + med ( B ) + med( C) = 360°
CONGRUÊNCIA DE TRIÂNGULOS
Em um triângulo qualquer, a medida de cada ângulo
externo é igual à soma das medidas dos ângulos
internos não-adjacentes a ele.


med (Â)= med ( b ) + med( c )
3
25/10/2016
Casos de congruência
2º caso: ALA ( ângulo, lado, ângulo)
1º caso: LAL ( lado, ângulo, lado)
Dois triângulos são congruentes quando possuem
os dois lados e o ângulo formado por esses lados
respectivamente congruentes.
Dois triângulos que possuem dois ângulos e o lado
compreendido
entre
esses
ângulos
respectivamente congruentes.
3º caso: LLL ( lado, lado, lado)
4º caso: LAAo ( lado, ângulo, ângulo
Dois triângulos são congruentes quando têm,
respectivamente, os três lados congruentes.
Dois triângulos são congruentes quando possuem
um lado, um ângulo adjacente a esses lado e o
ângulo
oposto
a
esse
mesmo
lado
respectivamente congruentes.
oposto)
4
25/10/2016
Pontos notáveis em um triângulo :
Altura
Obs: O ortocentro de um triângulo pode ser exterior ao
triângulo. Isso ocorre quanto o triângulo é obtusângulo.
É um segmento de reta que tem extremidades em um
dos vértices e no lado oposto a esse vértice, sendo
perpendicular a esse lado. Todo triângulo têm três
alturas.
O encontro das três alturas
de um triângulo é chamado
de ortocentro (H).
H
H
Mediatriz de um segmento
Mediana
Mediana de um triângulo é um segmento de reta
que tem extremidades no ponto médio de um lado e
no vértice oposto a esse lado. Todo triângulo tem 3
medianas.
É a reta que passa pelo ponto médio desse
segmento sendo perpendicular a ele.
O ponto de encontro das três
medianas é o baricentro (G).
A
M2
C
O baricentro divide a
mediana na razão de 2
para 1.
M3
G
M1
B
AG = 2.GM1
BG = 2.GM2
CG = 2.GM3
A
M
B
Essa reta é a mediatriz do
segmento AB. Qualquer ponto da
reta é eqüidistante de A e B.
5
25/10/2016
Mediatrizes de um triângulo
Bissetrizes de um triângulo
É a semirreta que divide esse ângulo em duas
medidas iguais.
O
A intersecção das três
mediatrizes é denominada
circuncentro (O).
Esse ponto é o centro da
circunferência circunscrita
ao triângulo.
I
A intersecção das três
bissetrizes de um triângulo é
denominada de incentro (I).
O incentro é o centro da
circunferência inscrita ao triângulo.
Resumindo:
* Ortocentro: intersecção das alturas.
* Baricentro: intersecção das medianas.
*Circuncentro: intersecção das mediatrizes. Centro da
circunferência circunscrita ao triângulo.
*Incentro: intersecção das bissetrizes. Centro da circunferência
inscrita.
Obs.:
Em alguns triângulos esses
pontos podem coincidir. No
triângulo equilátero, os
quatro pontos coincidem.
6