TRABALHO – 1 Trimestre

TRABALHO – 1o Trimestre
Disciplina: Matemática 1
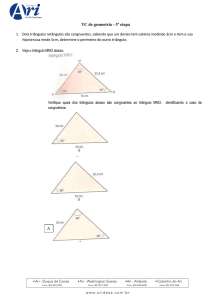
Série: 3o
Turma:
Data: 27.03.14
Professor: Sérgio Tambellini
Ensino: Médio
Trimestre: 1o
Valor: 3,0 ptos.
Nome:
no:
Nome:
no:
Nome:
no:
Nome:
no:
Nota:
- Leia atentamente as questões. - Redija suas respostas a tinta. - Não rasurar questões de múltipla escolha . - Evite rasuras.
“A educação para valores certamente supõe uma grande mudança na educação.” Projeto Semeando Valores e Cultivando Vidas.
Orientações do Trabalho
1) O trabalho pode ser feito individualmente, ou em grupos com 2, 3 ou 4 alunos no máximo;
2) Imprimir o trabalho (1 por grupo) em folhas tamanho A4 e preencher o cabeçalho;
3) Resolver as questões no próprio trabalho no espaço destinado em cada questão;
4) As resoluções deverão ser manuscritas (escritas à mão) obrigatoriamente;
5) Entregar o trabalho até a data que consta no cabeçalho do trabalho, após esta data o trabalho não será aceito;
6) O trabalho deverá ser entregue na sala de aula, na aula do Prof. Sérgio Tambellini, não podendo ser deixado no escaninho do
professor, nem na portaria do colégio;
7) Uma das questões do trabalho será colocada na 2a prova do 1o trimestre.
01. (MACKENZIE 2003 – Grupo I) Na figura, AB  AC e CE  CF . A medida de  é
a) 90º.
b) 120º.
c) 110º.
d) 130º.
e) 140º.
A
D
B

E
C
40º
F
02. (ITA/SP) Seja ABC um triângulo isósceles de base BC . Sobre o lado AC desse triângulo, considere um ponto D, tal que os
segmentos AD , BD e BC sejam todos congruentes entre si. Calcule a medida do ângulo BÂC.
03. (UFPI - 2000) No triângulo ABC (figura abaixo), os lados AB, AC e BC medem respectivamente 5cm, 7cm e 9cm. Se P é o ponto
de encontro das bissetrizes dos ângulos B e C e PQ//MB, PR//NC e MN//BC, a razão entre os perímetros dos triângulos AMN e PQR
é
a) 10/9.
b) 9/8.
c) 7/6.
d) 4/3.
e) 7/5.
04. (UNIRIO - 1996) Na figura, o triângulo ABD é equilátero, e seu lado mede 3m; H é o ortocentro, sendo que os pontos F e G são
pontos médios dos lados AD e BD respectivamente. Quantos rolos de fita adesiva serão necessários, no mínimo, para cobrir todos
os segmentos da figura, se cada rolo possui 1m de fita?
a) 18.
D
E
C
b) 20.
c) 22.
d) 24.
e) 26.
G
F
H
A
B
05. (SANTO ANDRÉ) O triângulo ABC é isósceles, com AB = AC. Nele está inscrito um triângulo DEF eqüilátero. Designando



o ângulo B F D por a, o ângulo A D E por b e o ângulo F E C por c, temos
ac
a) b 
.
2
a c
b) b 
.
2
bc
c) a 
.
2
ab
d) c 
.
2
bc
e) a 
.
2
A
E
D
b
c
a
B
F
C
06. (ENEM 2005) Quatro estações distribuidoras de energia A, B, C e D estão dispostas como vértices de um quadrado de 40 km de
lado. Deseja-se construir uma estação central que seja ao mesmo tempo equidistante das estações A e B e da estrada (reta) que liga as
estações C e D.
A nova estação deve ser localizada
a) no centro do quadrado.
b) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 15 km dessa estrada.
c) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 25 km dessa estrada.
d) no vértice de um triângulo equilátero de base AB, oposto a essa base.
e) no ponto médio da estrada que liga as estações A e B.
..::FIM::..