1. Números Complexos Introdução • Circuitos CC → somas

Campus I – João Pessoa
Disciplina: Análise
nálise de Circuitos
Curso Técnico Integrado em Eletrônica
Profª: Rafaelle Feliciano
Aula 02 – Álgebra Complexa
1. Números Complexos
Introdução
 Circuitos CC → somas algébricas de tensões e correntes;
 Circuitos CA → como se somam tensões e correntes senoidais?
 Aplicação de números complexos a formas de onda senoidais para determinar somas algébricas;
 Um número complexo pode ser representado por:
o Um sistema de eixos cartesianos = eixo real + eixo imaginário;
o Um ponto em um plano = forma retangular;
o Um raio vetor a partir da origem = forma polar;
 O símbolo j (ou algumas vezes i) é usado para denotar a parte imaginária
Forma Retangular
 Representação → (C = X +jY)
Y)
Figura 1 - Forma retangular de um número complexo
Exercícios
 Ex01 – Represente os seguintes números
nú
no plano complexo:
a. C = 3 + j4
b. C = 0 – j6
Forma Polar
 Representação → (C = Z ⁄ θ ) , Z = ( +
anti-horário a partir do eixo real positivo;
) é o módulo e θ é o ângulo medido no sentido
Figura 2 - Forma polar de um número complexo
1
 Para ângulos medidos no sentido horário, o ângulo tem sinal negativo (-θ);
 Números
úmeros complexos com sinal negativo = nº complexo OPOSTO ao complexo positivo, se (C
( =Z⁄
o
θ ), então (-C = Z ⁄ θ±180 )
Figura 3 – Efeito de um sinal negativo sobre a forma polar
Exercícios
 Ex02 – Represente os seguintes números no plano complexo:
a. C = 5 ⁄ 30o
b. C = 7 ⁄ -120o
Conversão entre as duas formas
 Retangular para polar
Z= (
+
)
e
=
 Polar para retangular
= .
e
= .
Exercícios
 Ex03 – Converta os números complexos abaixo para a forma polar:
a. C = 3 + j4
b. C = -6 + j3
 Ex04 – Converta os números complexos abaixo para a forma retangular:
a. C = 10 ⁄ -45o
b. C = 10 ⁄ 230o
Definições
 Por definição:
 Então,
=
 E, = . =
= √−1
1
. =− ;
=−
=
.
= −1
= 1;
=
.
= …
2
Complexo Conjugado
 Número complexo obtido quando se troca o sinal
sinal da parte imaginária (forma retangular) ou o
sinal do ângulo (forma polar);
∗
a. C = 2 + j3 →
∗
o
b. C = 2 ⁄ 30 →
=2− 3
= 2/−30
Figura 4 – Exemplos de complexos conjugados
Inverso ou Recíproco
 Inverso ou recíproco de um
m número complexo é 1 dividido pelo complexo;
ou
=
=
Operações matemáticas com complexos
 Adição
+
+
=
=
/
+
+
=(
+
)+ (
-
=
+
+
)
 Subtração
−
=(
=
−
+
)+ (
−
)
3
 Multiplicação
a. Forma Retangular
=
X
.
b. Forma Polar
=(
(
=
.
 Divisão
−
=
/ ) x (
=( .
+
+
)+ (
=
+
)
/ )
)/(
+
)
a. Forma Retangular
=
+
+
=
−
−
.
=
(
+
+
+
)+ (
+
−
)
b. Forma Polar
(
=
/ ) ÷ (
=
/
/
=
=
/(
/ )
−
)
Exercícios
 Ex05 – Efetue as seguintes operações:
a. (C1 = 2+j4) + (C2 = 3+j)
b. (C1 = 3+j3) - (C2 = -2+j5)
c. (C1 = 2+j3) . (C2 = 5+j10)
d. ( = 5/20 ) x ( = 10/30 )
e. (
= 50/0 ) x (C2 = j6)
f. (C1 = 1+j4) ÷(C2 = 4+j5)
g. ( = 15/10 ) ÷ ( = 2/7 )
4
2. Fasores
Introdução
 A adição de tensões e correntes senoidais é necessária quando analisamos circuitos CA;
 Método longo → traçar as duas formas de onda senoidais no mesmo gráfico e somar
algebricamente as ordenadas em cada ponto (figura 3);
Figura 5-- Adição ponto a ponto de duas formas de onda senoidais


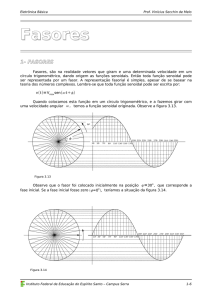
Método mais rápido → uso de vetor radial girante com módulo (comprimento) constante e
extremidade fixa na origem ((FASOR);
Fasor → É um número complexo associado a uma onda seno de fase deslocada tal que seu
módulo é o valor eficaz (rms) da tensão ou corrente,
te, e seu ângulo é o ângulo de fase da onda
seno de fase deslocada (forma polar);
polar)
o Forma fasorial de uma tensão ou corrente senoidal (freqüência não é representada)
= ⁄
= ⁄
Figura 6 - Representação fasorial de ondas senoidais
5
o
Álgebra de fasores (vetorial) só pode ser aplicada a formas de onda de mesma
freqüência;
o
Por razões práticas, se usam valores rms e não valores de pico na análise de circuitos
CA, portanto, o módulo do fasor é definido igual ao valor rms da função senoidal que
representa;
Diagrama de Fasores → Representação
ão (módulos e posições relativas) dos fasores
envolvidos na álgebra vetorial em t = 0s;
o

Para adicionar duas funções senoidais de tensão ou corrente, faz
faz-se a conversão para a forma
fasorial e calcula-se
se a soma usando álgebra de números complexos;
o
o
Resultado pode ou não ser transformado para obter uma função no domínio do
tempo;
Fasor é uma constante complexa e a senóide é uma função real do tempo, portanto;
3/30 ≠ 3√2
(
+ 30 )
Exercícios
 Ex01 (Boylestad, pg.432) – Escreva a expressão senoidal para os fasores a seguir se a freqüência
for 60Hz:
a. = 10⁄30
b. = 115⁄−70
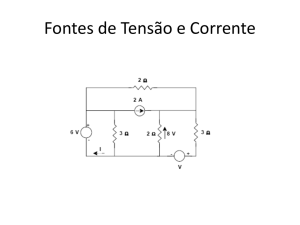
 Ex02 (Boylestad, pg.432) – Calcule a tensão de entrada no circuito
circuito abaixo, se:
se
= 50
e
(377 + 30 )
+
ein
-
= 30
+
va
-
(377 + 60 )
+
vb
-
 Ex03 (Boylestad, pg.441) – Determine a expressão senoidal para a corrente is no circuito abaixo,
sabendo que:
 Ex04 (Boylestad, pg.441) – Escreva as expressões a seguir na forma de fasores:
a.
√2(100)
(
+ 30
0 )
6
b.
c.
d.
( − 90 )
100
(377 + 0 )
42
( )
6 10
 Ex05 (O’Malley, pg.359) – Se duas correntes correspondem aos fasores
= 10⁄0 mA e
= 7⁄30 mA, qual o ângulo e o valor rms da corrente total que é a soma dessas correntes?
 Ex06 (O’Malley, pg.359) – Um motor síncrono solicita uma corrente de 9 A de uma fonte de
240V, 60 Hz. Um motor de indução em paralelo solicita 8 A. Se a corrente do motor síncrono
está adiantada da tensão aplicada de 20o e a corrente do motor de indução está atrasada dessa
tensão de 30o, qual a corrente total solicitada da fonte?
Fontes:
BOYLESTAD, R. L. – Introdução à Análise de Circuitos, 2004, 10ª edição, Ed. Prentice-Hall
O’MALLEY, J. – Análise de Circuitos, 1994. 2ª edição, Ed. McGraw-Hill
7