Fasores - Aprender

Eletrônica Básica
Prof. Vinícius Secchin de Melo
Fasores
1- FASORES
Fasores, são na realidade vetores que giram e uma determinada velocidade em um
círculo trigonométrico, dando origem as funções senoidais. Então toda função senoidal pode
ser representada por um fasor. A representação fasorial é simples, apesar de se basear na
teoria dos números complexos. Lembre-se que toda função senoidal pode ser escrita por:
v  t = Vmáx sen   t 
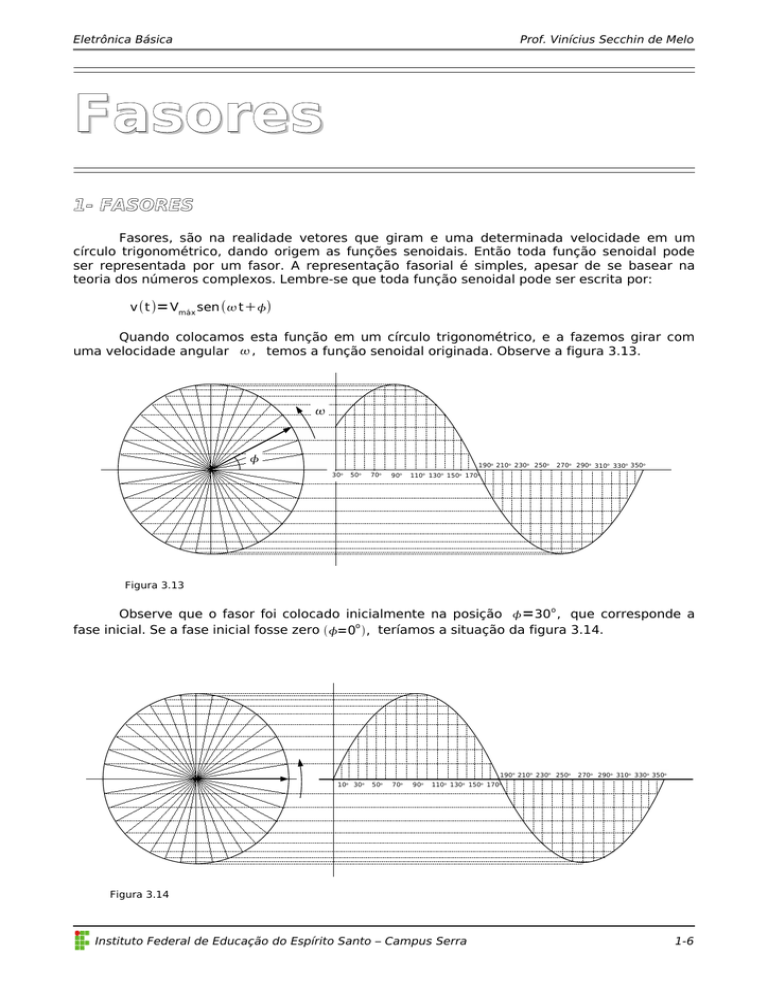
Quando colocamos esta função em um círculo trigonométrico, e a fazemos girar com
uma velocidade angular  , temos a função senoidal originada. Observe a figura 3.13.


190o 210o 230o 250o
30o
50o
70o
90o
270o 290o 310o 330o 350o
110o 130o 150o 170o
Figura 3.13
Observe que o fasor foi colocado inicialmente na posição  =30o , que corresponde a
fase inicial. Se a fase inicial fosse zero =0o , teríamos a situação da figura 3.14.
190o 210o 230o 250o
10o 30o
50o
70o
90o
270o 290o 310o 330o 350o
110o 130o 150o 170o
Figura 3.14
Instituto Federal de Educação do Espírito Santo – Campus Serra
1-6
Eletrônica Básica
Prof. Vinícius Secchin de Melo
Observe também que o tamanho do fasor é exatamente igual ao máximo atingido pela
função, ou seja, sua amplitude. A representação algébrica da notação fasorial é baseada na
teoria dos números complexos, porém iremos fazer uma simplificação da teoria, utilizando a
análise vetorial com um pouco de trigonometria para entendermos as operações com fasores.
Para isto vamos definir dois eixos (figura 3.15), um Real (eixo horizontal) e um
Imaginário (eixo vertical). Estes dois eixos formam o que chamamos matematicamente do
plano complexo ou plano imaginário.
Eixo
Imaginário
Plano
complexo
Eixo Real
Figura 3.15
A representação de um fasor no plano complexo é muito simples, basta transladarmos o
fasor do circulo trigonométrico para o plano complexo, atentos à fase inicial do fasor. Observe a
figura 3.16.
Eixo
Imaginário
Z
b

Eixo Real
a
Figura 3.16
No plano complexo o fasor pode ser representado por um número complexo Z, que
possui uma parte Real a, e uma parte imaginária b. Podemos também representá-lo através de
seu módulo (tamanho do fasor) e seu ângulo (fase do fasor). Esta duas formas de
representação dão origem as formas retangular e polar de se representar um número
complexo discriminadas a seguir.
- Forma retangular:
Na forma retangular o número complexo (nosso fasor) é representado a seguinte forma:
Z = {parte real} + j {parte imaginária}
Observe que o termo j representa na teoria dos números complexos a raiz de  −1 ,
porém em nosso estudo, somente será utilizado para identificar a parte imaginária de uma
notação fasorial.
Instituto Federal de Educação do Espírito Santo – Campus Serra
2-6
Eletrônica Básica
Prof. Vinícius Secchin de Melo
- Forma polar:
Na forma polar o número complexo (nosso fasor) é representado da seguinte forma:
Z = ∣Z∣/ 
/ 
Onde ∣Z∣ representa o módulo do número complexo, ou seja, o comprimento do fasor, e
representa a fase inicial do fasor.
Um número complexo Z qualquer, pode ser representado tanto em sua forma
retangular, como em sua forma polar, e a transformação de uma forma para outra não passa
de uma simples transformação trigonométrica. Observe a figura 3.17.
Eixo
Imaginário
Z
b

Eixo Real
a
Figura 3.17
O nosso número complexo Z pode ser representado pela sua forma polar, sendo então:
Z=∣Z∣/ 
Observe que a (parte Real) e b (parte Imaginária) são os catetos de um triângulo
retângulo e Z (módulo do fasor) a hipotenusa. Sendo assim, aplicando um pouco de
trigonometria, teremos:
A parte Real a do número complexo como sendo a projeção horizontal do fasor, dada
por:
a=∣Z∣cos 
Já a parte Imaginária b pode ser calculada como sendo a projeção vertical do fasor, dada
por:
b =∣Z∣sen 
Podemos também fazer o contrário, aplicando o Teorema de Pitágoras, podemos
calcular o módulo Z do número complexo, ou fasor, conhecendo suas partes Real e Imaginária.
Então:
2
Z
=a2 b2
Já a fase  pode ser obtida através da função trigonométrica tangente, pois:
tg  =
b
a
Instituto Federal de Educação do Espírito Santo – Campus Serra
3-6
Eletrônica Básica
Prof. Vinícius Secchin de Melo
Exemplo 1
______________________________________________________________________________________________________________________________________________________________________
Represente as seguintes funções senoidais na forma polar e retangular.
a) v(t) = 50 sen (1000t + 30o) V
forma polar:
o
V=50 / +30
V
Forma retangular:
o
a=50cos 30 =43,30
o
b=50sen 30 =25
V=43,30j25 V
b) i(t) = 2 sen (377t – 45o) A
forma polar:
o
i=2 / −45 V
Forma retangular:
o
o
a=2 cos−45 =1,414 e b=2 sen −45 =1,414
i=1,414j1 ,414 A
c) v(t) = 180 sen (377t + 90o) V
forma polar:
o
V=180 / +90
V
Forma retangular:
o
o
a=180 cos90 =0 e b=180 sen 90 =180
V=j180 V
d) i(t) = 10 sen (500t – 90o) A
forma polar:
o
i=10 / −90
A
Forma retangular:
o
o
a=10cos −90 =0 e b=10sen −90 =−10
i=−j10 A
e) v(t) = 75 sen 800t
forma polar:
o
V=75 / 0 V
Forma retangular:
o
o
a=75cos 0 =75 e b=75sen 0 =0
V=75 V
Instituto Federal de Educação do Espírito Santo – Campus Serra
4-6
Eletrônica Básica
Prof. Vinícius Secchin de Melo
2- Operações com fasores
As operações com fasores, ou números complexos são bem simples, sendo realizadas na
forma retangular ou polar:
- forma retangular
Sejam dois fasores
f 1=ajb e
f 2=c jd
A soma ou subtração na forma retangular é bem simples, pois a fazemos agrupando as
partes reais e as partes imaginárias, fazendo assim as operações com cada grupo. Sendo
assim:
f 1f2 =ajbcjd
f 1f2 =acjbd
f 1−f2 =ajb−cjd
f 1−f2 =ac−jbd
O produto pode ser feito aplicando a propriedade distributiva, então:
f 1 . f2=ajb.cjd
f 1 . f2=a.cj a.djb.cj.j b.d
Lembrando que
j= −1  j.j=  −1 .  −1=−1
f 1 . f2=a.c−b.dj a.db.c
A divisão não será apresentada aqui, pois sua resolução é muito complicada, sendo esta
feita na forma polar.
- forma polar
Na forma polar a soma e subtração são bem complicadas, portanto não citadas aqui,
porém a multiplicação e a divisão são extremamente simples comparadas a forma retangular.
Sejam dois fasores f 1=∣f 1∣/ 
e f 2=∣f 2∣/  .
O produto será dado por:
f 1 . f2=∣f1∣.∣f 2∣/ 
Enquanto a divisão:
f1 ∣f 1∣
=
/ −
f2 ∣f 2∣
Instituto Federal de Educação do Espírito Santo – Campus Serra
5-6
Eletrônica Básica
Prof. Vinícius Secchin de Melo
Exemplo 2
______________________________________________________________________________________________________________________________________________________________________
Sejam os seguintes fasores: f 1=2 j5,
o
f 2=4− j3,
a) f1 + f2
f 3=20 / 30
e f 4=5 / −45
o
. Determine:
b) f1 – f2
=2 j54− j3
=24j5− j3
=6 j2
=2 j5−4− j3
=2−4−j5− j3
=−2−j2
c) f1 . f2
o
f 1=2 j5 retangular⇒ polar f1=5,38 / 68,2
o
f 2=4− j3 retangular⇒ polar f2=5 / −36,8
o
o
=5,38.5 / 68,2 −36,8 
o
ou =25,26j15,42
=26,9 / 31,4
d) f 1÷f2
o
f 1=2 j5 retangular⇒ polar f1=5,38 / 68,2
o
f 2=4− j3 retangular⇒ polar f2=5 / −36,8
5,38
/ 68,2o−−36,8 o
5
o
ou =−0,27j1 ,04
=1,076 / 105
=
e) f3 + f4
o
f 3=20 / 30 polar ⇒ retangular f3=17,32 j10
o
f 4=5 / −45 polar⇒ retangular f4=3,53−j3 ,53
=17,32 j103,53−j3 ,53
=20,85j6 ,47 ou =21,83 / 17,23 o
f) f3 – f4
o
f 3=20 / 30 polar ⇒ retangular f3=17,32 j10
o
f 4=5 / −45 polar⇒ retangular f4=3,53−j3 ,53
=17,32 j10−3,53−j3 ,53
=13,79j13,53 ou =19,32 / 44,45 o
g) f3 . f4
o
o
=20.5 / 30 −45 
o
ou =96,59−j25 ,88
=100 / −15
h) f 3÷f4
20
/ 30o−−45o
5
o
ou =1,036j3 ,86
=4 / 75
=
Instituto Federal de Educação do Espírito Santo – Campus Serra
6-6