Aula 08 - Fasores

Centro Federal de Educação
C
ç Tecnológica
g de Santa
S
C
Catarina
Departamento de Eletrônica
Retificadores
Fasores
Prof. Clóvis Antônio Petry.
Florianópolis, agosto de 2007.
Bibliografia para esta aula
Capítulo 14
14:: Os Dispositivos Básicos e os Fasores
1. Fasores.
www.cefetsc.edu.br/~petry
Nesta aula
Seqüência
q
de conteúdos:
conteúdos:
1. Revisão;
2. Fasores.
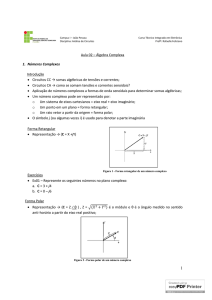
Forma retangular
C = X + j ⋅Y
Forma polar
C=Zθ
Conversão entre formas
Retangular
g
p
para p
polar
Z = X +Y
2
2
⎛Y ⎞
θ = tg ⎜ ⎟
⎝X⎠
−1
Polar para retangular
X = Z ⋅ cos (θ )
Y = Z ⋅ sen (θ )
Operações com o j
Por definição:
ç
j = −1
Daí:
j =
2
(
−1
)
1 ⎛1⎞ ⎛
= ⎜ ⎟⋅⎜
j ⎝ j⎠ ⎝
2
= −1
j⎞ j
j
=−j
⎟= 2 =
j⎠ j
−1
Adição de números complexos
A adição
ç de números complexos
p
é realizada facilmente na forma retangular:
g
C1 = ± X 1 ± jY1
C2 = ± X 2 ± jY2
C1 + C2 = ( ± X 1 ± jY1 ) + ( ± X 2 ± jY2 )
C1 + C2 = ( X 1 + X 2 ) + J (Y1 + Y2 )
Subtração de números complexos
A subtração
ç de números complexos
p
é realizada facilmente na forma retangular:
g
C1 = ± X 1 ± jY1
C2 = ± X 2 ± jY2
C1 − C2 = ( ± X 1 ± jY1 ) − ( ± X 2 ± jY2 )
C1 − C2 = ( X 1 − X 2 ) + J (Y1 − Y2 )
A adição e a subtração não podem ser realizadas na forma polar, a menos
que os números complexos tenham o mesmo ângulo θ ou que sua diferença
seja um múltiplo de 180º
180º.
Multiplicação de números complexos
A multiplicação
p
ç de números complexos
p
é realizada facilmente na forma p
polar:
C1 = Z1 θ1
(
C2 = Z 2 θ 2
)(
C1 ⋅ C2 = Z1 θ1 ⋅ Z 2 θ 2
C1 ⋅ C2 = Z1 ⋅ Z1 θ1 + θ 2
)
Divisão de números complexos
A divisão de números complexos
p
é realizada facilmente na forma p
polar:
C1 = Z1 θ1
C2 = Z 2 θ 2
C1 Z1 θ1
=
C2 Z 2 θ 2
C1 Z1
=
θ1 − θ 2
C2 Z 2
A multiplicação e a divisão podem ser realizadas com números complexos na
g
mas, no caso da divisão esta operação
p ç se torna bastante
forma retangular,
trabalhosa.
Fasores
Adição
ç de dois sinais variando no tempo,
p ,p
ponto a p
ponto:
Fasores
Fasor: vetor radial com módulo ((comprimento)
p
) constante e com a
extremidade fixa na origem.
Fasores
Adição
ç de duas tensões senoidais:
v ( t ) = Vm ⋅ sen (ωt ± θ )
Vm ±θ
Fasores
Adição
ç de duas tensões senoidais:
V1 = 1 0 V
o
V2 = 2 90 V
o
Vr = V1 + V2 = 1 0o + 2 90o
Vr = 2,, 236 63,, 43 V
o
Fasores
Adição
ç de duas correntes senoidais:
Fasores
A álgebra
g
dos fasores só p
pode ser aplicada
p
a formas de ondas
senoidais de mesma freqüência.
V = Vm θ v
I = I m θi
Fasores
Exemplo 14.30: Escreva a expressão senoidal para os fasores a seguir,
considerando que a freqüência é de 60 Hz:
a) I = 10 30o
b) I = 115 −70o
Exemplo 14.31: Calcule a tensão de entrada no circuito da figura a seguir:
va ( t ) = 50 ⋅ sen ( 377 ⋅ t + 300 ) ⎫⎪
H
⎬ 60 Hz
0
vb ( t ) = 30 ⋅ sen ( 377 ⋅ t + 60 ) ⎪⎭
Fasores
Exemplo 14.31: Calcule a tensão de entrada no circuito da figura a seguir:
ein ( t ) = va ( t ) + vb ( t )
ein ( t ) = 77,
77 43 ⋅ sen ( 377 ⋅ t + 41,17
41 17 0 ) V
Fasores
Exemplo 14.32: Determine a corrente i2 para o circuito mostrado a seguir:
Fasores
Exemplo 14.32: Determine a corrente i2 para o circuito mostrado a seguir:
i2 ( t ) = iT ( t ) + i1 ( t )
i2 ( t ) = 105,8
105 8 ⋅10−3 ⋅ sen (ωt + 100,89
100 890 ) A
Fasores
Exercícios: Da lista do final do capítulo 14:
- 48 à 53.
Na próxima aula
Capítulo 15
15:: Circuitos de CA em Série e em Paralelo
1. Revisão;
2. Introdução;
3 Impedância e o diagrama de fasores.
3.
fasores
www.cefetsc.edu.br/~petry