2.4. Função exponencial e logaritmo. Funções trigonométricas

34
Capítulo II: Funções Reais de Variável Real___________________________
2.4. Função exponencial e logaritmo. Funções trigonométricas
directas e inversas.
Função exponencial:
x
A uma função f : IR → IR definida por f ( x ) = a , onde a ∈ IR , a > 0 e a ≠ 1 , dá-se o
nome de função exponencial de base a.
Exemplos:
1
3
x
3
2
x
1
2
x
•
f (x ) = 2 x ; g (x ) =
•
f ( x ) = e x – esta função é particularmente importante pelas suas aplicações em
h( x ) =
;
;
i(x ) = 2 − x =
diversas áreas do conhecimento, nomeadamente na área da Economia.
Obs.:
•
O número “ e ” é irracional ( e = 2,71828182845
), e é conhecido por constante
de Euler
•
x
lim 1 +
n → +∞
n
n
= ex
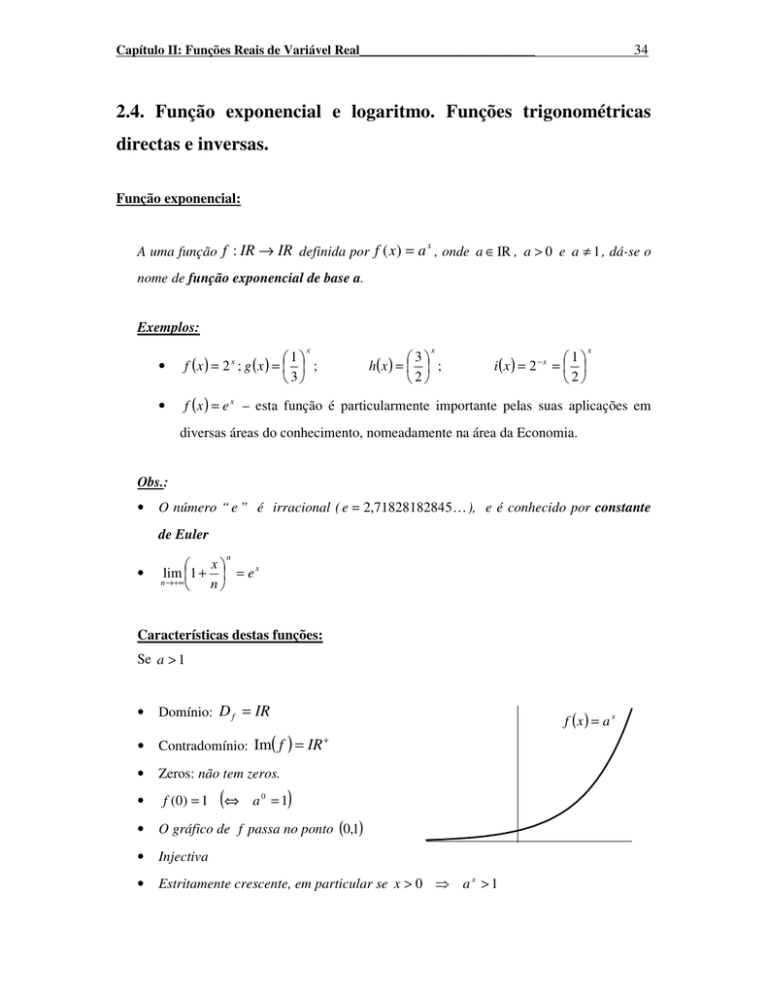
Características destas funções:
Se a > 1
•
Domínio: D f = IR
•
Contradomínio: Im( f ) = IR
•
Zeros: não tem zeros.
•
f (0 ) = 1
(⇔
f (x ) = a x
+
)
a0 = 1
•
O gráfico de f passa no ponto (0,1)
•
Injectiva
•
Estritamente crescente, em particular se x > 0
ax >1
Capítulo II: Funções Reais de Variável Real___________________________
35
Se 0 < a < 1
•
Domínio: D f = IR
•
Contradomínio: Im( f ) = IR
•
Zeros: não tem zeros.
•
f (x ) = a x
+
f ( 0) = 1
•
O gráfico de f passa no ponto (0,1)
•
Injectiva
•
Estritamente decrescente. (Note-se que agora a x > 1 quando x < 0 )
Função logaritmo:
A função inversa da função exponencial é a função
f : IR + → IR que se define por f ( x) = log a (x )
onde a ∈ IR , a > 0 e a ≠ 1 , à qual se dá o nome de função logaritmo de base a.
Obs.:
•
log a ( x ) representa o número y pelo qual se eleva a de modo a obter x , isto é,
log a (x ) = y
⇔
ay = x
Desta equivalência resulta também que
x=a
loga ( x )
e
•
log a ( x ) é a função inversa da função a x .
•
Notação:
( )
log a a y = y
log a (x ) logaritmo de base a
log( x )
logaritmo de base 10
ln (x )
logaritmo de base e , estes logaritmos chamam-se neperianos,
em homenagem ao matemático inglês Neper.
36
Capítulo II: Funções Reais de Variável Real___________________________
Características destas funções:
Se a > 1
+
• Domínio: D f = {x ∈ R : x > 0} = R
f ( x ) = log a ( x )
• Contradomínio: Im( f ) = IR
• Zeros: x = 1
(⇔
log a (1) = 0 )
• O gráfico passa no ponto (1,0)
• Injectiva e sobrejectiva (bijectiva)
• Estritamente crescente, em particular, se x < 1
log a ( x ) < 0
Exemplos:
•
f ( x) = log 2 (x )
•
g ( x) = log 10 ( x )
•
h( x ) = ln( x )
Se 0 < a < 1
+
• Domínio: D f = {x ∈ R : x > 0} = R
• Contradomínio: Im( f ) = IR
• Zeros: x = 1
(⇔
log a (1) = 0 )
f ( x ) = log a ( x )
• O gráfico passa no ponto (1,0)
• Injectiva e sobrejectiva (bijectiva)
• Estritamente crescente, em particular, se x < 1
Exemplos:
•
f ( x ) = log 0,5 ( x )
•
g ( x) = log1/ e ( x )
log a ( x ) < 0
Capítulo II: Funções Reais de Variável Real___________________________
37
Propriedades dos logaritmos:
•
log a ( xy ) = log a ( x ) + log a ( y )
•
log a
•
log a x
•
log a (a ) = 1
•
log a (1) = 0
•
log a ( x ) =
x
= log a (x ) − log a ( y )
y
( p ) = p log a (x)
ln ( x )
ln (a )
(fórmula de mudança de base)
Em particular, log 1 ( x ) =
e
ln ( x )
ln ( x )
=
= − ln (x )
1
ln (1) − ln (e )
ln
e
Exercícios:
1. O capital acumulado a prazo ao fim de n anos, quando capitalizado de forma contínua,
pode ser calculado através da função C(n) = C0 etn , em que C0 representa a quantidade
depositada e t a taxa de juro anual (na forma decimal).
Supondo C0 = 10000 euros e t = 5%, determine:
a. A quantidade acumulada ao fim de um, de dois e de quatro anos e meio.
b. Aproximadamente ao fim de quanto tempo duplica o capital?
2. O lucro L (em euros) obtido na venda de uma peça depende do número x de unidades
produzidas mensalmente. Esta relação é dada por
L( x) = log 10 +
x
.
4
a. Se a fábrica tiver a capacidade de produzir entre 500 e 800 unidades por mês, entre
que valores variará o lucro obtido em cada peça?
Capítulo II: Funções Reais de Variável Real___________________________
38
b. Qual deverá ser o número de unidades produzidas num mês para que o lucro unitário
seja 3 ?
3.
Seja f ( x) = ln(4 − x 2 ) .
a. Indique o domínio e contradomínio.
b. Classifique-a quanto à injectividade, monotonia e paridade.
c. Considere a função f definida em [0, 2 [. Caracterize a sua inversa (isto é, indique o
domínio e expressão analítica que define f
−1
)
Capítulo II: Funções Reais de Variável Real___________________________
Funções Trigonométricas (directas)
Considere-se um triângulo [ ABC ] rectângulo em A .
C
cateto oposto
a
b
hipotenusa
α
B
c
A
cateto adjacente
Seja α = ABˆ C , a = BC , b = AC , c = AB
Define-se:
senα =
b cateto oposto
=
a
hipotenusa
tgα =
cos α =
sen(α ) b
=
cos(α ) c
c cateto adjacente
=
a
hipotenusa
cotg α =
cos(α ) c
1
=
=
tg (α ) sen(α ) b
Obs.:
Alguns valores de referências destas funções:
θ radianos
0
π
senθ
0
1
cosθ
1
3
tgθ
0
3
cotg θ
-
6
2
2
3
3
π
4
2
2
1
1
2
2
π
3
3
1
π
2
π
1
0
2
0
-1
3
-
0
0
-
3
2
3
39
40
Capítulo II: Funções Reais de Variável Real___________________________
Função sen:
Seja α
π/2
um ângulo representado no
P = (cos α , sen α )
círculo trigonométrico (círculo de raio
1).
sen α
α
−π = π
Sen(α )
corresponde
ao
valor
0 = 2π
da
ordenada do ponto que resulta da
intersecção entre a circunferência e o
segmento que determina o ângulo com o
−π/2 = 3π/2
eixo dos xx’s (medido no sentido
contrário ao dos ponteiros do relógio), de acordo com a figura ao lado.
Assim, dado um ângulo α temos as
π/2
seguintes relações:
(i)
(ii)
+
sen(α ) = sen(π − α ) e
P = (cos α , sen α )
sen α = sen (π−α)
sen( −α ) = − sen(α )
Notar que a função seno toma valores
positivos nos 1º e 2º quadrantes e
valores negativos no 3º e 4º quadrantes.
+
π −α
−π = π
As relações anteriores permitem-nos
α
−
−
determinar o seno de qualquer ângulo
α conhecendo apenas o valor do seno
no 1º Quadrante.
Exemplo:
5π
∈ 3º quadrante mas
4
sen
5π (i )
5π
π (ii )
π
2
= sen π −
= sen −
= − sen
=−
4
4
4
4
2
0 = 2π
−π/2 = 3π/2
41
Capítulo II: Funções Reais de Variável Real___________________________
Como função real de variável real, temos
f : IR →
IR
x
sen( x)
À função f dá-se o nome de função seno.
(Obs: x é a medida de um ângulo em radianos)
O seu gráfico é
y
1
−2π
−3π/2
−π
−π/2
π/2
π
3π/2
2π
x
−1
Características desta função:
•
Domínio: IR;
•
Contradomínio: Im( f ) = [− 1,1] ;
•
Injectividade: não injectiva;
•
Zeros: x = kπ , k ∈ Z ;
•
Paridade: ∀x
•
Periodicidade: ∀x
•
Limitada: ∀x
•
Máximos: em x =
•
Mínimos: em x =
sen( − x) = − sen( x )
sen( x + 2π ) = sen( x)
− 1 ≤ sen( x) ≤ 1 ;
π
2
+ 2kπ , k ∈ Z ;
3π
+ 2kπ , k ∈ Z ;
2
(seno é uma função ímpar);
( 2π é o período positivo mínimo);
42
Capítulo II: Funções Reais de Variável Real___________________________
Função arcsen:
Consideremos a função
f : IR → [− 1,1]
x
sen( x )
Esta função não é injectiva
y
1
−3π/2
−2π
−π
−π/2
π/2
π
3π/2
x
2π
−1
Por exemplo, há infinitos pontos do domínio que têm por imagem zero
( sen( x ) = 0 ⇔
x = kπ , k ∈ Z ). Pelo que f não admite inversa.
Contudo, podemos considerar uma restrição do domínio onde a função seno seja
injectiva (chamada restrição principal):
g:
−
π π
,
2 2
x
→
[− 1,1]
sen( x)
cujo gráfico é:
y
1
−2π
−3π/2
−π
−π/2
π
π/2
3π/2
2π
x
−1
Assim definida, g é uma função injectiva e portanto faz sentido falar na sua inversa, g −1 .
Então g −1 tem por domínio
[− 1,1] ,
imagem
−
π π
,
2 2
e a cada x ∈ [− 1,1] faz
corresponder o ângulo (ou arco) cujo seno é x , que se representa por arcsen( x ) .
Capítulo II: Funções Reais de Variável Real___________________________
g −1 :
[− 1,1]
→
−
π π
,
2 2
arcsen( x)
x
cujo gráfico é
y
π/2
−1
1
x
−π/2
Características desta função:
•
Domínio: [− 1,1] ;
•
Imagem: −
•
Injectividade: injectiva;
•
Zeros: x = 0 ;
•
Paridade: ∀x
•
Monotonia: estritamente crescente;
•
Limitada: ∀x
•
Máximo em x = 1 ;
•
Mínimo em x = −1 ;
π π
;
,
2 2
arcsen(− x) = −arcsen( x )
−
π
2
≤ arcsen ( x) ≤
π
2
( arcsen é uma função ímpar);
;
Obs.:
•
O arcsen(x) é o valor real y tal que sen( y ) = x , onde x ∈ [− 1,1] , ou seja:
arcsen( x) = y ⇔ sen( y ) = x
•
sen(arcsen( x )) = x
onde − 1 ≤ x ≤ 1 ;
•
arcsen(sen( x )) = x
onde −
π
2
≤x≤
π
2
.
43
Capítulo II: Funções Reais de Variável Real___________________________
Exemplos:
1
2
sen arcsen
•
arcsen sen
•
arcsen sen
•
sen(arcsen(3)) = ?
π
2
1
2
=
•
=
2π
3
π
2
3
π
π π
2π
= pois
;
∉ − ,
2
3
3
2 2
= arcsen
(note que 3 ∉ …
Exercício 1:
Considere a função f definida em IR por:
f ( x) = cos
π
4
+ 2arcsen
x
2
Determine o domínio e contradomínio de f . Caracterize a inversa.
Resolução:
D f = x ∈ IR : −1 ≤
x
≤ 1 = {x ∈ IR : −2 ≤ x ≤ 2}= [− 2,2]
2
Determinemos o contradomínio de f :
−2≤ x ≤ 2 ⇔
⇔
x
≤1
2
x
≤ arcsen(1)
2
(notar que a função arcsen é crescente )
arcsen(−1) ≤ arcsen
π
⇔
−
⇔
− π ≤ 2arcsen
⇔
cos
⇔
Logo, Im( f ) =
−1 ≤
2
≤ arcsen
π
4
x
π
≤
2
2
x
≤π
2
− π ≤ cos
π
4
+ 2arcsen
x
π
≤ cos
+π
2
4
2
π
x
2
− π ≤ cos
+ 2arcsen
≤
+π
2
4
2
2
2
2
−π,
+π
2
2
44
Capítulo II: Funções Reais de Variável Real___________________________
45
f é uma função injectiva porque é composta de transformações injectivas
(exercício)
Comecemos por determinar a expressão analítica da inversa:
cos
π
+ 2arcsen
4
x
=y
2
x
π
= y − cos
2
4
⇔
2arcsen
⇔
arcsen
⇔
sen arcsen
⇔
y
x
2
= sen −
2
2 4
⇔
x = 2sen
y
x
2
= −
2
2 4
x
2
= sen
y
2
−
2 4
y
2
−
2 4
Portanto
f
−1
:
2
2
−π,
+π
2
2
[− 2,2]
→
x
2 sen
x
2
−
2 4
Exercício 2:
Dada a função: f ( x) =
π
3
+ 2arcsen 2 x − 1 .
Calcule D f e CD f . Verifique que f não tem zeros.
Resolução:
D f = {x ∈ IR : 2 x − 1 ≤ 1} = {x ∈ IR : −1 ≤ 2 x − 1 ≤ 1}
= {x ∈ IR : 0 ≤ 2 x ≤ 2}
= {x ∈ IR : 0 ≤ x ≤ 1}
= [0,1]
Determinemos a imagem de f :
0 ≤ x ≤ 1 ⇔ 0 ≤ 2x − 1 ≤ 1
⇔
π
3
+ 2arcsen(0) ≤
π
3
+ 2arcsen( 2 x − 1 ) ≤
π
3
+ 2arcsen(1)
Capítulo II: Funções Reais de Variável Real___________________________
Logo, Im( f ) =
π 4π
3
,
3
Vejamos agora que f não tem zeros:
f ( x) = 0 ⇔
π
3
+ 2arcsen 2 x − 1 = 0
π
⇔
arcsen 2 x − 1 = −
⇔
sen(arcsen 2 x − 1 ) = sen −
⇔
2x − 1 = −
6
π
6
1
2
f não tem zeros, pois a função módulo é sempre não negativa (isto é, ≥ 0 ).
Exercício 3:
Considere a função real de variável real definida por:
f ( x ) = arcsen
a) Verifique que D f = ]− ∞,−2] ∪ [0,+∞[ .
b) Determine a imagem de f
c) Caracterize a função inversa de f , f
−1
.
1
x +1
46
47
Capítulo II: Funções Reais de Variável Real___________________________
Função cos:
Seja α
um ângulo representado no
círculo trigonométrico (circulo de raio
1).
cos(α ) corresponde ao valor da abcissa do
ponto que resulta da intersecção entre a
circunferência e o segmento que determina
o ângulo com o eixo dos xx's , conforme
se pode ver na figura ao lado.
Recorrendo ao círculo trigonométrico, é fácil verificar as seguintes igualdade para um
determinado ângulo α :
π−α
cos( −α ) = cos(α )
α
cos(π − α ) = − cos(α )
π+α
α
cos(π + α ) = − cos(α )
Assim, usando as igualdades anteriores, é sempre possível determinar o valor do co-seno
de um ângulo α conhecendo apenas os valores da função co-seno no 1º quadrante.
Exemplo:
4π
∈ 3º quadrante mas
3
cos
4π
4π
1
π
π
= − cos π −
= − cos −
= − cos
=−
3
3
3
3
2
48
Capítulo II: Funções Reais de Variável Real___________________________
Como função real de variável real, temos
f : IR
x
→
IR
cos( x)
À função f dá-se o nome de função co-seno.
(obs: x é a medida de um ângulo em radianos)
O seu gráfico é
y
1
−2π
−3π/2
−π
−π/2
π/2
π
3π/2
2π
x
−1
Características desta função:
•
Domínio: IR;
•
Contradomínio: Im( f ) = [− 1,1] ;
•
Injectividade: não injectiva;
•
Zeros: x =
•
Paridade: ∀x
•
Periodicidade: ∀x cos( x + 2π ) = cos( x)
•
Limitada: ∀x
•
Máximos: em x = 2kπ , k ∈ Ζ ;
•
Mínimos: em x = π + 2kπ , k ∈ Ζ .
π
2
+ kπ , k ∈ Ζ ;
cos(− x) = cos(x)
−1 ≤ cos( x) ≤ 1 ;
(co-seno é uma função par);
( 2π é o período positivo mínimo);
49
Capítulo II: Funções Reais de Variável Real___________________________
Função arccos
Consideremos a função
f : IR → [− 1,1]
x
cos( x )
Esta função não é injectiva
y
1
−2π
−3π/2
−π
−π/2
π/2
π
3π/2
2π
x
−1
Por exemplo, há infinitos pontos do domínio que têm por imagem zero
( cos( x ) = 0 ⇔
x=
π
2
+ kπ , k ∈ Z ). Pelo que f não admite inversa.
Contudo, podemos considerar uma restrição do domínio onde a função co-seno seja
injectiva (chamada restrição principal):
g:
[0, π ]
→
x
[− 1,1]
cos( x)
cujo gráfico é:
y
1
−π/2
π/2
π
x
−1
Assim definida, g é uma função injectiva e portanto faz sentido falar na sua inversa, g −1 .
Então g −1 tem por domínio [− 1,1] , imagem [0, π ] e a cada x ∈ [− 1,1] faz corresponder o
ângulo (ou arco) cujo co-seno é x , que se representa por arccos( x ) .
Capítulo II: Funções Reais de Variável Real___________________________
g −1 :
[− 1,1]
[0, π ]
→
x
arccos( x)
cujo gráfico é
y
π
−1
1
x
Características desta função:
•
Domínio: [− 1,1] ;
•
Imagem: [0, π ] ;
•
Injectividade: injectiva;
•
Zeros: x = 1 ;
•
Paridade: nem é par nem é ímpar;
•
Monotonia: estritamente decrescente;
•
Limitada: ∀x ∈ [− 1,1]
•
Máximo em x = −1 ;
•
Mínimo em x = 0 ;
0 ≤ arccos ( x) ≤ π ;
Obs.:
•
O arccos( x) é o valor real y tal que cos( y ) = x , onde x ∈ [− 1,1] , ou seja:
arccos( x) = y ⇔ cos( y ) = x
•
cos(arccos( x )) = x
onde − 1 ≤ x ≤ 1 ;
•
arccos(cos( x )) = x
onde 0 ≤ x ≤ π .
50
Capítulo II: Funções Reais de Variável Real___________________________
Exemplos:
1
3
1
3
=
•
cos arccos
•
arccos cos
•
arccos cos
•
cos(arccos(− 2)) = ?
π
6
=
7π
6
π
6
= arccos −
3
5π
7π
=
pois
∉ [0, π ];
2
6
6
(note que − 2 ∉ …
Exercício 1:
Considere a função f definida por:
f ( x) =
π
3
arccos 2 x − 1
Determine o domínio e contradomínio de f . Caracterize a inversa, caso exista.
Resolução:
D f = {x ∈ IR : 2 x − 1 ≤ 1} = {x ∈ IR : −1 ≤ 2 x − 1 ≤ 1}
= {x ∈ IR : 0 ≤ 2 x ≤ 2}
= {x ∈ IR : 0 ≤ x ≤ 1}
= [0,1]
Determinemos o contradomínio de f :
0 ≤ x ≤1 ⇔
0 ≤ 2x ≤ 2
⇔
− 1 ≤ 2x − 1 ≤ 1
⇔
0 ≤ 2x − 1 ≤ 1
⇔
arccos(0) ≥ arccos 2 x − 1 ≥ arccos(1)
(notar que a função arccos é decrescente)
⇔ 0 ≤ arccos 2 x − 1 ≤
⇔ 0≤
Logo, Im( f ) = 0,
π
3
π2
6
π
2
arccos 2 x − 1 ≤
π2
6
51
52
Capítulo II: Funções Reais de Variável Real___________________________
A função f não admite inversa, pois não é injectiva:
1 3
, ∈ Df
4 4
1 3
≠
4 4
mas
f
1
π
=
4
3
2
= f
3
4
Exercício 2:
arccos(2 x + 1)
.
2
Dada a função: f ( x) = 1 −
(a) Calcule D f e CD f .
(b) Caracterize a inversa, caso exista.
(c) {x ∈ IR : f ( x ) = 0}
Resolução:
(a)
D f = {x ∈ IR : −1 ≤ 2 x + 1 ≤ 1} = {x ∈ IR : −2 ≤ 2 x ≤ 0}
= {x ∈ IR : −1 ≤ x ≤ 0}
= [− 1,0]
Determinemos a imagem de f :
− 1 ≤ x ≤ 0 ⇔ − 1 ≤ 2x + 1 ≤ 1
⇔ arccos(−1) ≥ arccos(2 x + 1) ≥ arccos(1)
⇔ 0 ≤ arccos(2 x + 1) ≤ π
arccos(2 x + 1)
π
⇔ 0≥−
≥−
2
2
π
arccos(2 x + 1)
⇔ 1− ≤1−
≤1
2
2
Logo, Im( f ) = 1 −
π
2
,1
(b) f é uma função injectiva porque é composta de funções injectivas.
1−
arccos(2 x + 1)
arccos(2 x + 1)
=y ⇔
= 1− y
2
2
⇔ arccos(2 x + 1) = 2(1 − y )
⇔ 2 x + 1 = cos(2 − 2 y )
⇔
Portanto
f −1 :
1−
π
2
x
,1
x=
→
− 1 + cos(2 − 2 y )
2
[− 1,0]
− 1 + cos (2 − 2 x )
2
Capítulo II: Funções Reais de Variável Real___________________________
(c) Estudemos os zeros de f
arccos(2 x + 1)
=0
2
arccos(2 x + 1)
=1
2
arccos(2 x + 1) = 2
2 x + 1 = cos(2)
− 1 + cos(2 )
x=
2
f ( x) = 0 ⇔ 1 −
⇔
⇔
⇔
⇔
f tem um zero em x =
− 1 + cos(2 )
.
2
53
54
Capítulo II: Funções Reais de Variável Real___________________________
Função tangente
Seja α um ângulo representado no círculo
trigonométrico.
(1,tg α)
tg (α ) corresponde ao valor da ordenada do
ponto
que
resulta
de
projectar
o
lado
extremidade do ângulo α no eixo paralelo ao
α
(1,0)
eixo das ordenadas e que passa pelo ponto de
coordenadas (1,0 ) . (ver figura ao lado)
Recorrendo ao círculo trigonométrico é fácil verificar as seguintes igualdades para um
determinado ângulo α :
α
−α
tg (−α ) = −tg (α )
tg (π − α ) = tg (− α )
Estas igualdades permitem calcular a tangente de um ângulo α conhecendo apenas os
seus valores no 1º quadrante.
Exemplo:
2π
∈ 2º quadrante
3
tg
2π
π
π
π
= tg π −
= tg −
= −tg
= 3
3
3
3
3
Capítulo II: Funções Reais de Variável Real___________________________
Como função real de variável real, temos
f : IR \
π
2
+ kπ , k ∈ Ζ
x
→
IR
tg ( x)
À função f dá-se o nome de função tangente.
(obs: x é a medida de um ângulo em radianos)
O seu gráfico é
Características desta função:
π
+ kπ , k ∈ Ζ ;
•
Domínio: IR \
•
Contradomínio: IR;
•
Injectividade: não injectiva;
•
Zeros: x = kπ , k ∈ Z ;
•
Paridade: ∀x tg (− x) = −tg ( x)
(tangente é uma função ímpar);
•
Periodicidade: ∀x tg ( x + π ) = tg ( x)
( π é o período positivo mínimo);
•
Limitada: não limitada;
•
Máximos: não tem;
•
Mínimos: não tem.
2
55
Capítulo II: Funções Reais de Variável Real___________________________
56
Função arcotangente
Consideremos a função
f : IR \
π
2
+ kπ , k ∈ Ζ
→
x
IR
tg ( x)
Esta função não é injectiva.
Por exemplo, há infinitos pontos do domínio que têm por imagem zero
( tg (x ) = 0 ⇔
x = kπ , k ∈ Z ). Pelo que f não admite inversa.
Contudo, podemos considerar uma restrição do domínio onde a função tangente seja
injectiva (chamada restrição principal):
g:
−
π π
,
2 2
x
→
IR
tg ( x)
cujo gráfico é:
Assim definida, g é uma função injectiva e portanto faz sentido falar na sua inversa, g −1 .
Então g −1 tem por domínio IR , imagem −
π π
,
2 2
e a cada x ∈ IR faz corresponder o
ângulo (ou arco) cuja tangente é x , que se representa por arctg ( x ) .
57
Capítulo II: Funções Reais de Variável Real___________________________
g −1 : IR →
x
−
π π
,
2 2
arctg ( x)
cujo gráfico é
y
π/2
π/4
−1
x
1
−π/4
−π/2
Características desta função:
•
Domínio: IR ;
•
Contradomínio: −
•
Injectividade: injectiva;
•
Zeros em x = 0 ;
•
Paridade: ∀x arctg (− x) = − arctg ( x )
•
Monotonia: estritamente crescente;
•
Limitada: ∀x
•
Máximos: não tem;
•
Mínimos: não tem;
−
π π
;
,
2 2
π
2
< arctg ( x) <
π
2
( arctg é uma função ímpar);
;
Obs.:
•
O arctg (x) é o valor real y tal que tg ( y ) = x , onde x ∈ IR , ou seja:
arctg ( x) = y ⇔ tg ( y ) = x
•
tg (arctg (x )) = x
onde x ∈ IR ;
•
arctg (tg (x )) = x
onde −
π
2
≤x≤
π
2
.
58
Capítulo II: Funções Reais de Variável Real___________________________
Exemplos:
•
tg arctg
•
arctg tg
•
arctg tg
1
7
=
π
=
6
7π
6
1
7
π
6
= arctg tg π +
π
= arctg tg
6
π
6
=
π
6
pois
7π
π π
.
∉ − ,
6
2 2
Exercício:
Considere a função definida por f ( x) = arctg
1
.
1 − 2x
Determine o domínio e contradomínio de f. Caracterize a inversa, caso exista.
Resolução:
D f = x ∈ IR :
1
1
∈ IR = {x ∈ IR : 1 − 2 x ≠ 0} = IR \
1− 2x
2
π π
Im( f ) = −
,
2 2
\ {arctg (0)} = −
π π
\ {0} pois
,
2 2
1
nunca se anula!
1− 2x
Nota: f é injectiva:
f ( x) = f ( y ) ⇔ arctg
⇔
1
1
= arctg
1 − 2x
1− 2y
1
1
=
1 − 2x 1 − 2 y
porque arctg é uma função injectiva (recordar!)
⇔
⇔
x=y
Determinemos a expressão analítica da inversa:
arctg
1
1
=y ⇔
= tg ( y )
1 − 2x
1 − 2x
⇔ 1 − 2 x = cot g ( y )
Portanto
f
−1
:
−
π π
,
2 2
x
\ {0} →
1
2
1 − cot g ( x)
2
IR \
⇔
⇔
x=
1 − cot g ( y )
2