Equações Modulares

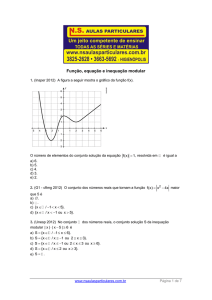
Equações Modulares
1. (Espcex (Aman) 2015) O número de soluções da
1
3
equação | x | ⋅ | x − 3 |= 2 ⋅ x − , no conjunto , é
2
2
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
2. (Ufsc 2014) Assinale a(s) proposição(ões)
CORRETA(S).
x −1
é
x+3
01) O domínio da função f dada por f(x) =
{x ∈ ; x ≥ 1}.
02) O único valor inteiro que pertence à solução da
inequação x2 − 4x + 3 < 0 é 2.
04) O conjunto solução da equação modular
| 3 − 2x |=| x − 2 | é S = {1}.
− x, se x < 0

08) A função R(x) =  x 2 , se 0 ≤ x ≤ 1 é crescente em
1, se x > 1

todo o seu domínio.
16) Se uma função f : →
é simultaneamente par
e ímpar, então f(1) = 0.
32) Os gráficos das funções f : → e g : → ,
dadas respectivamente por f(x) = x 2 e g(x) = 2 x ,
para todo x real, se intersectam em exatamente
um único ponto.
64)
a) 10
b) 7
c) 0
d) 3
e) 4
6. (G1 - cftmg 2013) A soma das raízes da equação
2
modular x + 1 − 5 x + 1 + 4 = 0 é
a) – 7.
b) – 4.
c) 3.
d) 5.
7. (Esc. Naval 2013) A soma das raízes reais distintas
da equação x − 2 − 2 = 2 é igual a
a) 0
b) 2
c) 4
d) 6
e) 8
8. (Unioeste 2012) Seja S o conjunto solução de
∣
3
−2 ∣ + 4x −  
2
2
−2
20
−
5 < 1.
É correto afirmar que S é igual a:
a) S = {x ∈ ; − 1 < x < 1}.
{
}
7
11
<x<
.
18
18
c) S = {x ∈ ; x > −1} .
b) S = x ∈ ; −
{
}
1
7
<x<
.
2
16
e) S = {x ∈ ; x < 10} .
x 2 = x para todo x real.
d) S = x ∈ ; −
3. (Fuvest 2014) Sobre a equação
2
(x + 3)2 x −9 log | x 2 + x − 1|= 0, é correto afirmar que
a) ela não possui raízes reais.
b) sua única raiz real é −3.
c) duas de suas raízes reais são 3 e −3.
d) suas únicas raízes reais são −3 , 0 e 1.
e) ela possui cinco raízes reais distintas.
4. (Espcex (Aman) 2014) Se Y = {y ∈
Letra
Número
n
tal
que 6y − 1 ≥ 5y − 10}, então:
1

a) Y =  −∞, 
6

b) Y = {−1}
c) Y =
d) Y = ∅
1

e)  , +∞ 
6


A
B
C
D
E
...
W
X
Y
Z
1
2
3
4
5
...
23
24
25
26
Para utilizar o sistema, cada número n,
correspondente a uma determinada letra, é
transformado em um número f(n), de acordo com a
seguinte função:
 2n + 3, se 1 ≤ n ≤ 10
f (n ) = 
50 − n, se 11 ≤ n ≤ 26
5. (Udesc 2014) A soma das raízes distintas da
equação x2 − 5x + 6 = x − 3 é:
www.soexatas.com
9. (Uerj 2012) Para enviar mensagens sigilosas
substituindo letras por números, foi utilizado um
sistema no qual cada letra do alfabeto está associada
a um único número n, formando a sequência de 26
números ilustrada na tabela:
Página 1
na qual n ∈
As letras do nome ANA, por exemplo, estão
associadas aos números [1 14 1]. Ao se utilizar o
sistema, obtém-se a nova matriz [f(1) f(14) f(1)],
gerando a matriz código [5 36 5].
Considere a destinatária de uma mensagem cujo
nome corresponde à seguinte matriz código: [7 13 5
30 32 21 24].
Identifique esse nome.
10. (Uepb 2012) A soma das raízes que a equação
modular x − 2 − 7 = 6 é
a) 15
b) 30
c) 4
d) 2
e) 8
c)
11. (Ita 2011) O produto das raízes reais da equação
2
|x – 3x + 2| = |2x – 3| é igual a
a) –5.
b) –1.
c) 1.
d) 2.
e) 5.
12. (G1 - col.naval 2011) No conjunto dos números
reais, o conjunto solução da equação
4
( 2x + 1)
4
= 3x + 2
14. (Ita 2007) Sobre a equação na variável real x,
│ │ │ x - 1 │ - 3 │ - 2 │ = 0,
a) é vazio.
b) é unitario.
c) possui dois elementos.
d) possui três elementos.
e) possui quatro elementos.
13. (Ufmg 2010) Considere a função f ( x )= x 1 − x .
Assinale a alternativa em que o gráfico dessa função
está CORRETO.
podemos afirmar que
a) ela não admite solução real.
b) a soma de todas as suas soluções é 6.
c) ela admite apenas soluções positivas.
d) a soma de todas as soluções é 4.
e) ela admite apenas duas soluções reais.
15. (Ufjf 2006) Sobre os elementos do conjunto2
solução da equação │ x │ - 4 │ x │ - 5 = 0, podemos
dizer que:
a) são um número natural e um número inteiro.
b) são números naturais.
c) o único elemento é um número natural.
d) um deles é um número racional, o outro é um
número irracional.
e) não existem, isto é, o conjunto-solução é vazio.
16. (Uem 2004) Considerando o conjunto A = {x ∈ R; 3 ≤ x ≤ 3}, assinale a(s) alternativa(s) correta(s).
2
01) O conjunto das soluções da inequação x < 9 é
igual ao conjunto A.
02) O conjunto A contém o conjunto das soluções da
2
inequação - 5x - 14x + 3 ≥ 0.
04) A reunião dos conjuntos das soluções das
2
equações (5x - 8) = - 21 e |5x – 3| = - 8 está
contida em A.
08) O conjunto-solução da equação |x – 5| = |8x + 3|
está contido no conjunto A.
16) O menor elemento do conjunto A pertence à
interseção dos conjuntos das soluções das
2
2
inequações x ≤ 9 e x - 7x + 10 ≥ 0.
a)
b)
www.soexatas.com
d)
Página 2
32) A interseção entre o conjunto A e o conjunto das
2
soluções da inequação x - 7x + 10 ≤ 0 é o
conjunto B = {x ∈ R; 2 ≤ x < 3}.
17. (Ufv 2002) Se x e y são números reais quaisquer,
então é CORRETO afirmar que:
2
2
a) se x < y , então x < y.
2
2
b) se x < y, então x < y .
2
2
c) se x - y = 0, então │x│ = │y│.
e) - x < 0.
2
18. (Ufmg 2000) Considere a equação (x - 14x + 38)
2
= 11 .
2
O número de raízes reais DISTINTAS dessa equação
é
a) 1
b) 2
c) 3
d) 4
19. (Fatec 2000) A igualdade -│-x │ = -(-x) é
verdadeira para todos os elementos do conjunto
a) IR
b) { x ∈ IR │ x ≥ 0}
c) { x ∈ IR │ x ≤ 0}
d) { x ∈ IR │ 0 ≤ x ≤10}
e) { x ∈ IR │ -3 ≤ x ≤ 3}
2
20. (Ufpi 2000) A soma das raízes da equação │x│ +
2 │x│ - 15 = 0 é:
a) 0
b) -2
c) -4
d) 6
e) 2
www.soexatas.com
Página 3
Resolução das Questões
[32] Incorreto. Como f(2) = g(2) = 4,
segue-se que o ponto (2, 4) é
Resposta da questão 1:
[D]
x2 − 3 ⋅ x
2(2x − 3)
1
3
| x | ⋅ | x − 3 |= 2 ⋅ x − ⇒
=
⇒ x 2 − 3x = 4x − 6 ou x 2 − 3x = −2x + 6 ⇒
2
2
2
2
x 2 − 7x + 6 = 0 ou x 2 − x − 6 = 0 ⇒ x = 1 ou x = 6 ou x = −3 ou x = 2
Portanto, a equação possui quatro raízes.
Resposta da questão 2:
02 + 16 = 18.
[01] Incorreto. Lembrando que uma função está bem
definida apenas quando se conhece o seu
domínio, o contradomínio e a lei de associação,
vamos supor que a proposição seja:
O maior subconjunto dos números reais para o
x −1
, está
qual a função f, dada por f(x) =
x+3
definida é {x ∈ ; x ≥ 1}.
Desse modo,
comum aos gráficos de f e de g. Além disso, há
pelo menos mais um ponto de interseção no
1

intervalo  −1, −  . Com efeito, note que f é
2


decrescente e g é crescente para x ∈ ] − ∞, 0[.
 1
 1
Logo, sendo f( −1) > g( −1) e f  −  < g  −  ,
2


 2
segue que os gráficos de f e de g apresentam
pelo menos um ponto de interseção no intervalo
1

 −1, − 2  (esboce os gráficos para concluir que


existe um único ponto nesse intervalo).
[64] Incorreto. Suponhamos por absurdo que
x 2 = x, para todo x real. Nesse caso, teríamos
x = x2 = ( − x)2 = − x, o que obviamente vale
apenas para x = 0. Na verdade,
x real.
x 2 = | x |, para todo
Resposta da questão 3:
[E]
x −1
≥ 0 ⇔ x < −3 ou x ≥ 1
x+3
2
Como 2x −9 > 0 para todo x real, vem
e, portanto, o maior subconjunto dos números
reais para o qual a função f está definida é
{x ∈ ; x < −3 ou x ≥ 1}.
(x + 3)2x
2
−9
log | x 2 + x − 1| = 0 ⇔ (x + 3)log | x 2 + x − 1| = 0
x+3 = 0
⇔
[02] Correto. Tem-se
ou
2
| x + x − 1| = 1
x2 − 4x + 3 < 0 ⇔ (x − 1) ⋅ (x − 3) < 0
⇔
⇔ 1 < x < 3.
x = −3
ou
x 2 + x − 1 = 1 ou x2 + x − 1 = −1
Portanto, a única solução inteira da inequação
x 2 − 4x + 3 < 0 é x = 2.
⇔
x = −3
.
ou
(x = 1 ou x = −2) ou (x = 0 ou x = −1)
[04] Incorreto. Sabendo que | a | = | b | ⇒ a = ±b, vem
Portanto, a equação dada possui 5 raízes reais
distintas.
| 3 − 2x | = | x − 2 | ⇒ 3 − 2x = ±(x − 2)
⇒ x = 1 ou x =
5
.
3
Resposta da questão 4:
[C]
 5
Por conseguinte, S = 1,  .
 3
[08] Incorreto. A função f é decrescente para x < 0.
[16] Correto. Se f é simultaneamente par e ímpar,
então f( − x) = f(x) e f( −x) = −f(x), para todo x
real. Daí, segue-se que f(x) = f( − x) = 0 para todo
x real.
www.soexatas.com
Página 4
3
−2 ∣ + 4x −  
2
2
∣
⇒−
Resposta da questão 5:
[E]
−2
−
20
5
< 1⇒
4
−2
2
2
9
< 1 ⇒ 2x − < 1 ⇒ −1 < 2x − < 1 ⇒
2
9
9
2 + 4x −
7
11
<x<
18
18
Resposta da questão 9:
De acordo com as informações, temos que
Fatorando, obtemos
f(n1 ) = 7 ⇔ 2n1 + 3 = 7 ⇔ n1 = 2,
2
x − 5x + 6 = | x − 3 | ⇔ (x − 2) ⋅ (x − 3) = | x − 3 | .
Se x ≥ 3, então | x − 3 | = x − 3. Assim,
f(n2 ) = 13 ⇔ 2n2 + 3 = 13 ⇔ n2 = 5,
f(n3 ) = 5 ⇔ 2n3 + 3 = 5 ⇔ n3 = 1,
2
(x − 2) ⋅ (x − 3) = x − 3 ⇔ (x − 3) = 0 ⇔ x = 3.
f(n4 ) = 30 ⇔ 50 − n4 = 30 ⇔ n4 = 20,
Se x < 3, então | x − 3 | = −(x − 3). Daí,
f(n5 ) = 32 ⇔ 50 − n5 = 32 ⇔ n5 = 18,
(x − 2) ⋅ (x − 3) = −(x − 3) ⇔ (x − 3) ⋅ (x − 1) ⇔ x = 1 ou x = 3.
e
Mas x = 3 não convém, pois x < 3.
Por conseguinte, a soma das raízes distintas da
equação é 1 + 3 = 4.
Resposta da questão 6:
[B]
f(n7 ) = 24 ⇔ 50 − n7 = 24 ⇔ n7 = 26.
Portanto, o nome da destinatária é Beatriz.
Resposta da questão 10:
[E]
Resolvendo a equação na incógnita x + 1 temos:
x +1 =
f(n6 ) = 21 ⇔ 2n6 + 3 = 21 ⇔ n6 = 9
5±3
⇒ x + 1 = 4 ou x + 1 = 1 ⇒ x = 3 ou x = -5 ou x = 0 ou x = -2
2
Temos
x − 2 − 7 = 6 ⇔ x − 2 − 7 = ±6.
Logo,
Calculando a soma das raízes, temos:
3 + ( −5 ) + 0 + ( −2 ) = −4
| x − 2 | = 13 ⇔ x − 2 = ±13
⇔ x = 15 ou x = −11
ou
Resposta da questão 7:
[D]
| x − 2 | = 1 ⇔ x − 2 = ±1
⇔ x = 3 ou x = 1.
x − 2 − 2 = 2 ou x − 2 − 2 = −2
x − 2 = 4 ou x − 2 = 0
Portanto, o resultado é 15 + ( −11) + 3 + 1 = 8.
x − 2 = 4 ou x − 2 = −4 ou x = 2
x = 6 ou x = −2 ou x = 2
Portanto, a soma das raízes será 6 + ( − 2) + 2 = 6.
Resposta da questão 11:
[A]
2
Resposta da questão 8:
[B]
www.soexatas.com
2
x – 3X + 2 = 2x – 3 ⇔ x – 5x + 5 = 0, temos o
produto das raízes igual a 5.
2
2
x – 3x + 2 = -2x + 3 ⇔ x + x - 1 = 0, temos o produto
das raízes igual a -1.
Página 5
Logo, o produto total das raízes é -1.5 = -5
Resposta da questão 20:
[A]
Resposta da questão 12:
[B]
4
( 2x + 1)4
= 3x + 2 ⇒ | 2x + 1| = 3x + 2
⇒ 2x + 1 = ±(3x + 2)
3
⇒ x = −1ou x = − .
5
Mas, como | y | ≥ 0, y ∈ , segue que
2
3x + 2 ≥ 0 ⇔ x ≥ − . Então, o único valor de x que
3
3
2
satisfaz a equação dada é − , pois −1 < − .
5
3
Resposta da questão 13:
[B]
0
x–x
2
1
x–x
2
2
x -x
Resposta da questão 14:
[D]
Resposta da questão 15:
[A]
Resposta da questão 16:
alternativas corretas: 02, 04, 08 e 16
alternativas incorretas: 01 e 32
Resposta da questão 17:
[C]
Resposta da questão 18:
[C]
Resposta da questão 19:
[C]
www.soexatas.com
Página 6