1º Banco de Questões do 4º Bimestre de Matemática

Aluno(a):
__
Professora: Deise Ilha
Componente Curricular: Matemática
.
Turno: Matutino.
Data:
/
/ 2016.
1º Banco de Questões do 4º Bimestre de Matemática (REVISÃO)
QUESTÃO 01
Tipo A (Julgar Certo ou Errado)
Conteúdo: Altura, mediana, bissetriz de um triângulo
Julgue C (Certo) ou E (errado).
a)
b)
c)
d)
e)
Ceviana é qualquer segmento de reta que une um vértice ao seu lado oposto ou prolongamento.
Altura: segmento que une um vértice com um ponto do suporte do lado oposto, sendo este
segmento perpendicular ao suporte.
O ponto de encontro das alturas chama-se ortocentro.
Mediana: segmento que une o vértice ao ponto médio do lado oposto.
O ponto de encontro das medianas chama-se baricentro.
QUESTÃO 02
Tipo A (Julgar Certo ou Errado)
Conteúdo: Altura, mediana, bissetriz de um triângulo
Julgue C (Certo) ou E (errado).
a)
b)
c)
d)
e)
Num triângulo retângulo, a mediana relativa à hipotenusa é igual a metade da hipotenusa.
Bissetriz Interna: é o segmento que une o vértice a um ponto do lado oposto, dividindo o ângulo
interno em duas partes congruentes.
O ponto de encontro das bissetrizes chama-se incentro.
O incentro é o centro do círculo inscrito no triângulo.
O segmento formado pelos pontos médios de dois lados de um triângulo é paralelo ao terceiro lado
e mede a metade dele (terceiro lado).
QUESTÃO 03
Tipo C (Marcar)
Conteúdo: Altura, mediana, bissetriz de um triângulo
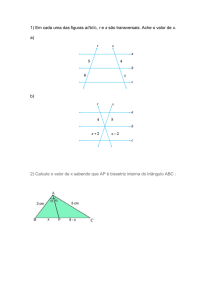
No triângulo abaixo, AM é mediana relativa ao lado BC. O perímetro do triângulo ABC é:
a)
b)
c)
d)
32 cm.
104 cm.
200 cm.
310 cm.
QUESTÃO 04
Tipo C (Marcar)
Conteúdo: Propriedades do triângulo isósceles e do triângulo equilátero
̅̅̅̅ , qual é o valor de x?
̅̅̅̅ ≅ 𝐶𝐷
Na figura, o triângulo ABC é equilátero. Sabendo que 𝐵𝐷
a)
b)
c)
d)
60º.
72º.
102º.
180º.
QUESTÃO 05
Tipo C (Marcar)
Conteúdo: Altura, mediana, bissetriz de um triângulo
(UCSal-BA) A cidade de Boncomeço está situada na confluência de duas rodovias, a BR1 e a BR2, conforme
representado na figura.
A telefonia celular está chegando a Boncomeço, e a empresa responsável pela instalação do sistema pretende
colocar a central de transmissão no cruzamento das duas rodovias. Além disso, planeja também instalar uma
série de torres de trasmissão/recepção sobre uma linha reta partindo de Boncomeço, de maneira que cada torre
seja equidistante da BR1 e da BR2.
Considerando que as semirretas que contêm as duas rodovias e a semirrreta com as bases das torres estão no
mesmo plano, então as bases das torres serão instaladas em uma semirreta denominada:
a)
b)
c)
d)
bissetriz.
mediana.
Mediatriz.
tangente.
QUESTÃO 06
Tipo D (Dissertativa)
Conteúdo: Altura, mediana, bissetriz de um triângulo
Responda:
a) Se os lados de um  ABC isósceles são AB = 4,2 cm, AC = 4,2 cm e AB = 67 mm, calcule o seu perímetro.
b) Na figura, o triângulo ABD é congruente ao triângulo CBD. Calcule x e y. (Figura I)
c) Um dos ângulos internos de um triângulo isósceles mede 100°. Qual é a medida do ângulo agudo formado
pelas bissetrizes dos outros ângulos internos?
d) O triângulo ABC é isóscele de base BC. Sabendo que AB = 3x – 10, BC = 2x + 4 e AC = x + 4, calcule a
medida de BC. (Figura II)
̅̅̅̅ a altura do triângulo ABC, calcule x e y. (Figura III)
e) Sendo 𝐴𝐻
Figura I
(letra b)
QUESTÃO 07
Figura II
(letra d)
Figura III
(letra e)
Tipo D (Dissertativa)
Conteúdo: Os ângulos no triângulo
Determine, x e cada triângulo.
a)
b)
c)
d)
e)
f)
QUESTÃO 08
Tipo D (Dissertativa)
Conteúdo: Altura, mediana, bissetriz de um triângulo
̅̅̅̅ . Calcule a medida de 𝛼. (Figura
a) Na figura, o triângulo ABC é retângulo em 𝐴̂ e M é o ponto médio do lado 𝐵𝐶
I)
̅̅̅̅ é a bissetriz interna. Calcule a medida α. (Figura II)
b) Na figura, M é o ponto médio do lado ̅̅̅̅
𝐵𝐶 e 𝐶𝑁
c) Na figura, o triângulo ABC é congruente ao triângulo CDE. Determine o valor  e de : (Figura III)
d) Observe a figura a seguir. Nessa figura, AD = BD, o ângulo C mede 60° e DÂC é o dobro do ângulo B. Quanto
mede o ângulo B. (Figura IV)
e) Determine o valor de x, sabendo que AD e BC são bissetrizes dos ângulos indicados. (Figura V)
f) Na figura, o ABC é congruente ao EDC. Determine o caso de congruência e o valor de x e y. (Figura VI)
Figura I
(letra a)
Figura II
(letra b)
Figura III
(letra c)
Figura IV
(letra d)
Figura V
(letra e)
Figura VI
(letra f)
E
D
C
x
20°
A
QUESTÃO 09
B
Tipo D (Dissertativa)
Conteúdo: Os ângulos no triângulo
Determine, x e cada triângulo.
g)
h)
i)
j)
k)
l)
QUESTÃO 10
Tipo D (Dissertativa)
Conteúdo: Os ângulos no triângulo
Calcule, x e y.
“A Matemática apresenta invenções tão sutis que poderão servir não só para satisfazer os curiosos
como, também para auxiliar as artes e poupar trabalho aos homens”. (Descartes)