Pontos notáveis no triângulo – Exercícios de aplicação

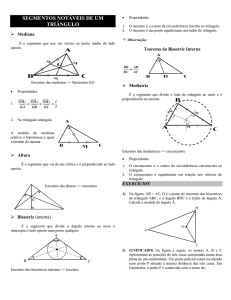
Pontos notáveis no triângulo – Exercícios de aplicação
1. Nas afirmações abaixo, assinale (B) para baricentro, (I) para incentro, (C) para circuncentro e (O) para
ortocentro, sobre as propriedades dos pontos notáveis nos triângulos.
( ) eqüidistante dos lados do triângulo
( ) ponto de encontro das mediatrizes
( ) divide cada mediana na razão 2:1
( ) ponto de encontro das bissetrizes internas
( ) ex-incentro – ponto de encontro das bissetrizes do triângulo órtico
( ) ( ) podem estar internos, sobre ou externos ao triângulo
( ) centro da circunferência circunscrita
( ) ponto de encontro das medianas
( ) eqüidistante dos vértices do triângulo
( ) ponto de encontro das retas suportes das alturas
( ) centro da circunferência inscrita
2. Num triângulo ABC retângulo em Â, um dos ângulos mede 20º. Pergunta-se:
a) qual o ângulo formado pela mediana e pela bissetriz do ângulo reto ?
b) qual o ângulo formado pela mediana relativa à hipotenusa e pela bissetriz do maior ângulo agudo do triângulo ?
3. Na figura, BI e CI são bissetrizes internas do triângulo ABC. Se  = 40º calcule a medida de BÎC.
4. Na figura abaixo, ABC é um triângulo retângulo em Â, M é ponto médio de BC e MN é paralelo à AB. Se
BC = 18 cm, calcule a medida de AP.
C
A
B
5. Na figura abaixo DE é paralelo à BC e contém o incentro do triângulo ABC. Se AB = 10 cm, AC = 14 cm e
BC = 17 cm, calcule o perímetro do triângulo ADE.
A
D
B
E
C