matemática

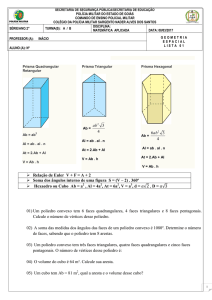
6.º ANO
SEGUNDO CICLO
A
C
I
ÁT
M
E
T
MA
PTM6_20131833_P001_020_4P.indd 1
ANTÓNIO SOUSA
MARIA JOÃO MATOS
SÓNIA MONTEIRO
TERESA PINTO
3/5/14 2:48 PM
ÍNDICE
UNIDADE
UNIDADE
Figuras geométricas planas
Sólidos geométricos
Relacionar circunferências com ângulos, retas e polígonos
Exercícios resolvidos
Exercícios propostos
O perímetro e a área de polígonos regulares e de círculos
Exercícios resolvidos
Exercícios propostos
Teste de avaliação 4
6
8
10
12
15
19
Identificar sólidos geométricos e reconhecer as suas propriedades
Exercícios resolvidos
Exercícios propostos
Medir volumes de sólidos geométricos e resolver problemas
Exercícios resolvidos
Exercícios propostos
Teste de avaliação UNIDADE
UNIDADE
Números naturais
Potências de expoente natural
Números primos
Crivo de Eratóstenes
Decomposição em fatores primos
Aplicações da decomposição em fatores primos
Exercícios resolvidos
Exercícios propostos
48
48
49
50
53
56
Potências de expoente natural
Cálculo de potências
Expressões numéricas
Exercícios resolvidos
Exercícios propostos
Teste de avaliação UNIDADE
UNIDADE
Sequências e regularidades
Isometrias no plano
Sequências e regularidades
Exercícios resolvidos
Exercícios propostos
Proporcionalidade direta
Exercícios resolvidos
Exercícios propostos
Teste de avaliação 76
78
81
84
87
93
96
Construir e reconhecer propriedades de isometrias do plano
Exercícios resolvidos
Exercícios propostos
Teste de avaliação UNIDADE
UNIDADE
Representação e tratamento
de dados
Números racionais
Organizar e representar dados
Exercícios resolvidos
Exercícios propostos
Teste de avaliação 2
PTM6_20152402_TXT_P001_020_1P.indd 2
116
121
124
128
22
26
29
33
35
38
44
60
61
64
66
70
73
100
105
109
113
Representar e comparar números racionais
Adicionar números racionais
Subtrair números racionais
Exercícios resolvidos
Exercícios propostos
Teste de avaliação 132
136
138
139
144
149
Teste de avaliação global 1 Teste de avaliação global 2
Soluções 152
157
161
ISBN 978-989-647-687-8
7/2/15 11:07 AM
RESUMO TEÓRICO
2.1. IDENTIFICAR SÓLIDOS GEOMÉTRICOS E RECONHECER
AS SUAS PROPRIEDADES
© AREAL EDITORES
MATEMÁTICA | 6.º ANO
POLIEDROS
Poliedro convexo
Poliedro não convexo
Um poliedro diz-se convexo quando qualquer segmento de reta que
una dois pontos do poliedro está nele contido.
Prisma
Base
Vértice
Face lateral do prisma
Aresta
Base
Paralelepípedo retângulo
Um prisma é um poliedro com duas faces geometricamente iguais (que
chamamos bases do prisma) situadas respetivamente em dois planos
paralelos de modo que as restantes faces sejam paralelogramos.
Os prismas classificam-se em triangulares, quadrangulares, pentagonais, …
quando possuem, respetivamente, bases triangulares, quadrangulares, pentagonais, …
PRISMA TRIANGULAR
PRISMA QUADRANGULAR
PRISMA HEXAGONAL
POLIEDRO
POLÍGONO DA BASE
22
PTM6_20131833_P021_046_4P.indd 22
3/5/14 2:49 PM
SÓLIDOS GEOMÉTRICOS
MATEMÁTICA | 6.º ANO
RESUMO TEÓRICO
Num prisma se o ângulo formado entre as
faces laterais e as bases for reto o prisma
diz-se reto. Quando este ângulo não é
reto o prisma diz-se oblíquo. As faces
laterais de um prisma reto são retângulos.
Prisma reto
Prisma
oblíquo
Prisma oblíquo
Prisma reto
Prisma reto
e regular
Um prisma reto diz-se regular quando as suas bases forem polígonos regulares.
Pirâmide
Vértice
Face lateral da pirâmide
Aresta
Base
Pirâmide quadrangular
Uma pirâmide é um poliedro determinado por um polígono (base da
pirâmide) que constitui uma das suas faces e um ponto (vértice da
pirâmide), exterior ao plano que contém a base de tal modo que as
restantes faces são triângulos determinados pelo vértice da pirâmide e pelos lados da base.
As pirâmides classificam-se em triangulares, quadrangulares, pentagonais, …
quando possuem, respetivamente, bases triangulares, quadrangulares, pentagonais, …
PIRÂMIDE TRIANGULAR PIRÂMIDE QUADRANGULAR PIRÂMIDE PENTAGONAL
© AREAL EDITORES
POLIEDRO
POLÍGONO DA BASE
23
PTM6_20131833_P021_046_4P.indd 23
3/5/14 2:49 PM
MATEMÁTICA | 6.º ANO
12.7.(9 - 6)2 * 11 12.8.42 * 43 : 25
12.9.104 * 103 : 102 + 3
12.10.63 : 33 * 22
12.11.2 * (4 + 10 )
5
5
4
12.12. - a b + 3a42 : a b b
2
2
5
2
2
2
3
2
© AREAL EDITORES
EXERCÍCIOS PROPOSTOS
13.Um comboio de mercadorias tem 10 carruagens.
Cada carruagem transporta 10 caixotes. Cada caixote leva 10 bonecas, que possuem 10 vestidos
diferentes cada.
13.1. Traduz este problema sob a forma de uma potência.
13.2.Calcula o número de vestidos de bonecas que o
comboio transporta.
13.3. Comenta a afirmação: “O comboio transporta 1000 bonecas.”
14. Na figura temos dois terrenos quadrados de áreas diferentes.
6m
3m
Terreno I
Terreno II
14.1. Escreve na forma de potência a medida de área de cada um dos terrenos.
14.2.Escreve uma expressão que traduza a diferença entre a medida de área do
terreno II e a medida de área do terreno I.
14.3.Determina o valor da expressão 32 + 62 e indica o seu significado no contexto do problema.
14.4. Indica, justificando, o valor lógico da proposição: 32 * 62 = 184.
14.5.Calcula o quociente entre a medida de área do terreno II e a medida de área
do terreno I e indica-o na forma de potência.
15.Num supermercado há 33 caixas de chocolate, cada
caixa tem 32 bombons de chocolate. Quantos bombons de chocolate existem no supermercado?
16. Investiga se é possível escrever o número 33 como potência de base 3.
Justifica a tua resposta.
17. Descobre quatro números naturais seguidos que verifiquem a relação
a3 + b3 + c3 = d3.
72
PTM6_20131833_P059_074.indd 72
3/6/14 6:25 PM
POTÊNCIAS DE EXPOENTE NATURAL
MATEMÁTICA | 6.º ANO
TESTE DE AVALIAÇÃO
Ao longo do teste vais encontrar questões de escolha múltipla e de desenvolvimento:
– para cada uma das perguntas de escolha múltipla são indicadas quatro alternativas, das quais só uma está
correta.
– nas questões de desenvolvimento deves apresentar todos os cálculos e todas as justificações necessárias.
1.
Observa com atenção a tabela.
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
1.1. Identifica com X os números primos.
1.2. Assinala com ˚ os múltiplos de 4 e com O os múltiplos de 7.
1.3. Com base no item anterior indica o mínimo múltiplo comum entre 4 e 7.
2.
Considera os números: 2, 4, 7, 20 e 24.
2.1. Indica todos os números primos e compostos.
2.2. Decompõe o número 20 em fatores primos.
2.3. Determina o m.m.c. (2, 20).
2.4. Determina o m.d.c. (4, 24).
2.5.2 * 2 * 2 * 3 é um número divisível por:
(A) 2
3.
O número 2,5 representado na forma de fração irredutível é:
(A) 25
10
(B) 5
(B) 5
10
(C) 7
5
(C) 2
(D) 9
(D) 2
5
4.Dois ciclistas partem em simultâneo do mesmo local para efetuarem uma
corrida num circuito fechado. Um deles leva 4 minutos a percorrer o circuito e o outro 6 minutos. Quanto tempo demoram a encontrar-se novamente no ponto de partida?
© AREAL EDITORES
5.Um professor levou a sua turma de 6.º ano a uma visita de estudo a uma
fábrica de doces. A fábrica ofereceu 54 chocolates e 36 caramelos. O professor distribuiu os doces em saquinhos para oferecer aos seus alunos, tendo
o cuidado de colocar em cada saquinho o mesmo número de doces de
cada tipo.
5.1. Indica, justificando, o maior número de alunos que a turma pode ter.
5.2. Quantos chocolates e quantos caramelos havia em cada saco?
73
PTM6_20131833_P059_074_4P.indd 73
3/5/14 2:49 PM