Fórmulas de Geometria

 Geometria Plana
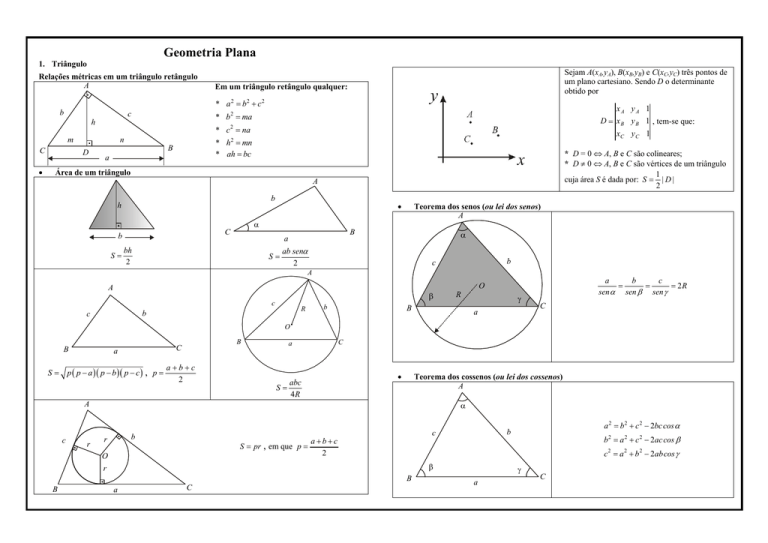
1. Triângulo
Relações métricas em um triângulo retângulo
A
Sejam A(xA,yA), B(xB,yB) e C(xC,yC) três pontos de
um plano cartesiano. Sendo D o determinante
obtido por
Em um triângulo retângulo qualquer:
* a 2 = b2 + c 2
b
h
•
n
D
D = x B y B 1 , tem-se que:
* c 2 = na
m
C
xA yA 1
* b 2 = ma
c
xC y C 1
* h2 = mn
* ah = bc
B
a
* D = 0 ⇔ A, B e C são colineares;
* D ≠ 0 ⇔ A, B e C são vértices de um triângulo
1
cuja área S é dada por: S = | D |
2
Área de um triângulo
A
b
h
•
Teorema dos senos (ou lei dos senos)
A
α
C
b
S=
B
a
bh
2
S=
α
ab senα
2
b
c
A
a
b
c
=
=
= 2R
sen α sen β sen γ
O
A
β
c
R
b
c
b
R
B
γ
a
C
O
B
B
C
a
S = p ( p − a )( p − b )( p − c ) , p =
a+b+c
2
C
a
S=
•
abc
4R
Teorema dos cossenos (ou lei dos cossenos)
A
α
A
c
r
b
r
S = pr , em que p =
O
a+b+c
2
β
B
a
C
b 2 = a 2 + c 2 − 2ac cos β
c 2 = a 2 + b 2 − 2ab cos γ
r
B
a 2 = b 2 + c 2 − 2bc cos α
b
c
γ
a
C
•
Diagrama de inclusão dos quadriláteros
Teorema da bissetriz
Interna
Quadriláteros
Externa
Trapézios
A
α
A
β
α
Paralelogramos
Losangos
β
Retângulos
Quadrados
B
B
C
C
pé da bissetriz interna
S
S
pé da bissetriz externa
AB AC
=
BS CS
AB AC
=
BS CS
3. Polígonos
2. Quadriláteros
•
Áreas dos quadriláteros notáveis
A1
Trapézio
β1
Paralelogramo
b
An
a
h
h
S=
( B + b) h
A6
S = a⋅h
2
Losango
Retângulo
Quadrado
β6
A3
* a soma dos ângulos externos é Se = 360°
Em um polígono regular de n lados:
A4
Si ( n − 2 )180°
=
n
n
Se 360°
=
* cada ângulo externo é β =
n
n
β5
* cada ângulo interno é α =
A5
4. Círculo
•
a
Áreas das partes do círculo
Coroa circular
Círculo
d
b
α5
n ( n − 3)
2
* a soma dos ângulos internos é Si = ( n − 2 )180°
* o número de diagonais é d =
β4
α4
α6
a
α1
α3
b
B
A2
β3
α2
αn
βn
b
Em um polígono convexo de n lados:
β2
Setor circular
b
R
D
a
S = a ⋅b
S=
d ⋅D
2
O
R
R
S=
α R
r
2
* S = π R2
* C = 2π R
C
CR αR 2
, α em radianos
S=
=
2
2
(
S = π R2 − r 2
)
•
Ângulos em um círculo
Ângulo central ( α ) e
ângulo inscrito ( β )
Geometria Espacial
1.
Prisma
Ângulo excêntrico exterior
Ângulo excêntrico interior
base
Em um prisma qualquer:
P
P
A
* o volume é V = ( área da base ) × ( altura )
β
D
D
β
* a área lateral ( A ) é a soma das áreas das faces
laterais
* a área da base ( AB ) é a área de apenas uma base
aresta lateral
C
A
α
O
α
* a área total é AT = 2 AB + A
aresta da base
C
base
B
A
B
B
α=
( )
α = 2β = med AB
AB + CD
2
• Prismas particulares
Cubo
a
a
AB − CD
β=
2
a
•
Conseqüência importante
P é externo
A
C
A
B
a
P
P
( PA)( PB ) = ( PC )( PD )
c
a+c =b+d
* Diagonal do cubo: D = a 3
*
*
*
*
c
D
d
B
( PA)( PB ) = ( PC )( PD )
* Diagonal de uma face: d = a 2
d
a
a
Paralelepípedo reto-retângulo
a
b
b
c
D
* Área total: AT = 6 a 2
a
D
b
C
D
* Área lateral: A = 4 a 2
a
Potência de um ponto P em relação a uma circunferência
P é interno
* Área da base: AB = a 2
b
b
a
2.
Volume: V = a 3
Soma das dimensões: a + b + c
Soma das arestas: 4a + 4b + 4c
Área total: AT = 2(ab + ac + bc )
* Diagonal: D = a 2 + b 2 + c 2
* Volume: V = abc
* Relação importante: ( a + b + c ) = D 2 + AT
2
Cilindro circular reto
r
r
2πr
A = 2πrh
g=h
2πr
r
* Área da base: AB = πr 2
* Área total: AT = 2πr (r + h )
* Volume: V = AB h = πr 2 h
h=g
* Área lateral: A = 2πrh
*
a
Diagonal: d = a 2
a
a
a
a
3. Pirâmide
V
Em uma pirâmide qualquer:
apótema da pirâmide
altura
aresta
lateral
1
* o volume é V = ⋅ AB ⋅ h
3
* a área lateral ( A ) é a soma das áreas
das faces laterais
* a área total ( AT ) é AT = AB + A
4.
Cone circular reto
raio do setor circular
g
g
g
g
h
A = πrg
r
apótema da base
r
aresta da base
•
2πr
Sólidos importantes
*
Tetraedro regular
a2 3
Área da base: AB =
4
H
3a 2 3
4
*
Área lateral: A =
*
Área total: AT = a 2 3
*
a 6
Altura: H =
3
*
a3 2
Volume: V =
12
*
Área total: AT = 2a 2 3
*
Volume: V =
a
a
a
raio da
base
a
Octaedro regular
a3 2
3
Em qualquer cone circular reto:
* g 2 = h2 + r 2
*
5.
a área da base é AB = πr 2
* a área total é AT = πr (r + g )
* o volume é V =
1 2
πr h
3
Esfera
O
•
* a área lateral é A = πrg
Partes da esfera
R
* Área da superfície esférica: A = 4πR 2
4
* Volume da esfera: V = πR 3
3
Cunha esférica
A
e
Fuso esférico
e
A
Cunha esférica
R
R
O
O
h
r
O
θ
R
Calota esférica é
só a superfície
Fuso esférico
Zona esférica é
só a superfície
R
R
θ
R
B
4
2π ∼ πR3
2θR3
⇒V =
,
3
3
θ ∼ S ( volume da cunha )
B
2π ∼ 4πR 2
⇒ S = 2θR 2 ,
θ ∼ S ( área do fuso )
θ em radianos
Segmento esférico de uma base
θ em radianos
Segmento esférico de duas bases
e
e
* Área (S): S = 2πRh
* Área (S): S = 2πRh
6. Razão de semelhança de dois sólidos
e
V
Quando dois sólidos S1 e S 2 (como
os da figura) são semelhantes de
razão linear k
V'
h
~
r
r1
h
O
D
O
r
h
r2
C
D'
O'
A
(S1)
(S2)
[(
)
]
* Volume (V): V =
(
πh 2
3r + h 2
6
* Área (S): S = 2πRh + πr 21 + πr2 2
* Área (S): S = 2 πRh + πr 2
Tronco de pirâmide de bases paralelas
Calota esférica
Zona esférica
)
Sendo Ab a área da base menor, AB a área da
aresta lateral
altura
* a razão entre dois elementos
lineares quaisquer é k
* a
razão
entre
as
áreas
correspondentes é k 2
* a razão entre os volumes é k 3
B
base menor
πh
3 r12 + r22 + h 2
6
C'
B'
A'
O
7.
* Volume (V): V =
O
h
base maior
base maior, A a área lateral, h a altura e V o
volume do tronco, tem-se que:
* a área lateral A é a soma das áreas das faces
laterais
* a área total é AT = AB + Ab + A
* o volume é V =
(
h
AB + Ab + AB Ab
3
)
h
8.
Tronco cone de revolução de bases paralelas
10. Teorema de Pappus-Guldin
g
e
*
r
r
geratriz
altura
2πR
g
h
2πr
G
g
*
Figura plana
de área S
R
R
Superfície desenvolvida
do tronco
Sendo Ab a área da base menor, AB a área
da base maior, A a área lateral, g a geratriz,
h a altura e V o volume do tronco, tem-se
que:
* Ab = πr 2
*
A B = πR
A = πg (R + r )
*
* AT = AB + Ab + A
*V =
(
)
(
h
πh 2
AB + Ab + AB Ab =
R + r 2 + Rr
3
3
)
2
*
Seja S a área de uma figura plana. Ao girar essa figura plana
(de 360o) em torno do eixo e, obtém-se um sólido de
revolução. Demonstra-se que o volume desse sólido pode
ser calculado pela fórmula V = 2πdS . Sendo G o centro de
gravidade da figura, d é a distância do ponto G à reta e.
*
É vantagem aplicar a fórmula
V = 2πdS quando o centro de
gravidade da figura é de fácil
determinação.
Em qualquer triângulo, o centro de
gravidade é o seu baricentro.
Em qualquer quadrado, losango ou
paralelogramo, o centro de
gravidade é a intersecção das suas
diagonais.
Em qualquer polígono regular, o
centro de gravidade é o centro da
circunferência
inscrita
(ou
circunscrita).
11. Poliedros
Poliedro convexo
Em um poliedro convexo com F
faces, V vértices e A arestas:
9. Princípio de Cavalieri
Princípio de Cavalieri para áreas
d1
d2
F1
s
F2
r
* V − A+ F = 2
* S = (V − 2 ) 360° , em que S é a soma
"Sejam F1 e F2 duas figuras planas
apoiadas sobre uma mesma reta r. Se
toda reta s, paralela a r, determina em
F1 e F2 segmentos d1 e d 2
congruentes (os segmentos d1 e d 2 são
as intersecções da reta s como as figuras
F1 e F2 ), então as figuras F1 e F2 são
equivalentes (têm áreas iguais).
dos ângulos das faces de um poliedro
convexo
•
Poliedros de Platão (há apenas 5 poliedros de Platão):
S2
β
A1
A2
"Sejam S1 e S 2 dois sólidos apoiados
sobre um mesmo plano α . Se todo
plano β , paralelo a α , secciona S1 e
S2
segundo
equivalentes
α
figuras
( A1 = A2 ) ,
planas
então
os
sólidos S1 e S 2 têm volumes iguais."
Um poliedro é de Platão somente se:
1o) todas as suas faces são polígonos com
o mesmo número de lados;
2o) em cada um de seus vértices concorre o
mesmo número de arestas;
3o) é Euleriano.
* tetraedros
* hexaedros
* octaedros
* dodecaedros
* icosaedros
O princípio de Cavalieri
S1
Classificação
Poliedros Regulares
Um poliedro é regular somente se:
o
1 ) todas as suas faces são polígonos
regulares e congruentes
2o) possui todos os ângulos poliédricos
congruentes
Observações importantes
Tetraedro regular
Hexaedro regular
*
*
Octaedro regular
Dodecaedro regular
Icosaedro regular
São os poliedros de Platão com todas
as faces formadas por polígonos
regulares
"Todo poliedro regular é de Platão,
mas nem todo poliedro de Platão é
regular."