UNIVERSIDADE DO EXTREMO SUL CATARINENESE
UNESC
CURSO DE PÓS-GRADUAÇÃO ESPECIALIZAÇÃO EM EDUCAÇÃO
MATEMÁTICA
VIVIANE RAUPP NUNES DE ARAÚJO
A FILOSOFIA DA EDUCAÇÃO MATEMÁTICA NA FORMAÇÃO DOS
PROFESSORES DO ENSINO FUNDAMENTAL E MÉDIO
CRICIÚMA, NOVEMBRO DE 2005
VIVIANE RAUPP NUNES DE ARAÚJO
A FILOSOFIA DA EDUCAÇÃO MATEMÁTICA NA FORMAÇÃO DOS
PROFESSORES DO ENSINO FUNDAMENTAL E MÉDIO
Monografia apresentada à Diretoria de Pósgraduação da Universidade do Extremo Sul
Catarinense- UNESC, para a obtenção do título
de especialista em Educação Matemática.
Orientador: Prof.(Dr). Ademir Damazio
CRICIÚMA, NOVEMBRO DE 2005.
Para Paulo, Paula e Maria Laura.
Pela esperança, alegria e ternura
que renovam em mim a cada dia.
AGRADECIMENTOS
Este
trabalho,
além
do
esforço
pessoal,
contou
com
inúmeras
contribuições, as quais sou eternamente grata.
Aos meus pais, pela existência e por terem cultivado em mim o dom da
persistência.
A minha família, pela compreensão, paciência e esforço compartilhado.
Ao professor Ademir Damazio, que com sabedoria, e respeito às minhas
idéias, soube indicar o caminho a ser trilhado.
Aos amigos, Fábio, Josilete e Franciane, que em muitos momentos
fizeram deles o meu trabalho
Aos meus colegas de especialização, em especial para Maria Aparecida,
Daiana Souza e Jaqueline, companheiras nas horas boas e ruins...
As colegas da Escola de Educação Básica João Dagostim pelo apoio,
incentivo e oportunidade da pesquisa.
Antes de começar quero lavar-me da
suspeita de ingratidão para com meus
mestres. O ensino que critico é tanto
o que ministrei como o que recebi.
(REVUZ, s/d, p. 70)
RESUMO
Nesta pesquisa, relatamos nossas investigações acerca dos entendimentos que
duas professoras de Matemática uma do Ensino Fundamental e outra do Ensino
Médio - apresentam com relação à formação de professores tendo como base as
diversas concepções de Filosofia da Educação Matemática. A pesquisa foi realizada
em uma escola pública estadual localizada no bairro Quarta Linha, município de
Criciúma SC. O objetivo foi analisar as perspectivas do ensino da Matemática a
partir da ação docente e as concepções que os educadores têm com relação ao
ensino e à Filosofia da Educação Matemática. Os dados coletados para o
desenvolvimento deste trabalho foram obtidos através de reuniões entre as
professoras de matemática da escola, com o objetivo de preparar as atividades de
aprendizagem a serem incluídas no projeto trimestral desenvolvido na escola no 2º
trimestre de 2004. Também serviram de instrumentos de coletas de dados as
conversas informais, (sala dos professores) e as observações das aulas com as
respectivas professoras. As atividades desenvolvidas em sala de aula nos
permitiram apontar quais correntes filosóficas se manifestam conforme as atividades
propostas. Da mesma forma, quais as concepções de ensino e de formação de
professores que se manifestam na prática pedagógica destas professoras. Para que
analisássemos os dados obtidos, resultantes das observações feitas nas aulas,
efetuamos uma série de leituras referente ao objeto pesquisado. Tudo isso com a
finalidade de adquirirmos fundamentação teórica adequada, objetivando
compreender e analisar tais informações com maior aproximação possível. Assim
sendo, pudemos identificar os encontros e desencontros entre teoria e prática
pedagógica, e da mesma forma, a filosofia que fundamenta as perspectivas e as
concepções que as educadoras têm com relação ao ensino da Matemática baseada
na Filosofia da Educação Matemática.
Palavras-chave: Filosofia da matemática, concepções de ensino, formação de
professores.
SUMÁRIO
1 INTRODUÇÃO ........................................................................................................ 08
2 FILOSOFIA DA EDUCAÇÃO MATEMÁTICA - Significações que servem de
esclarecimento para uma forma de pensar e conceber a educação matemática .................................................................................................................................... 17
2.1 Filosofia ............................................................................................................... 17
2.2 Filosofia da Educação........................................................................................ 21
2.3 Filosofia da Matemática.....................................................................................25
2.2.1 Logicismo......................................................................................................... 27
2.2.2 Formalismo......................................................................................................39
2.2.3 Intuicionismo...................................................................................................49
3 AULAS DE MATEMÁTICA: QUE FILOSOFIA? .................................................... 58
3.1 Caracterização da Escola .................................................................................. 58
3.2 Primeira Aproximação ....................................................................................... 61
3.3 Acompanhamento das aulas - Observações, Invetigações, Dúvidas - Que
filosofia é esta?........................................................................................................62
4 CONCLUSÃO.......................................................................................................... 74
REFERÊNCIAS .......................................................................................................... 79
1 INTRODUÇÃO
As mudanças pelas quais o ensino da matemática passou ao longo dos
tempos acabaram por refletir fortemente na formação dos professores da
contemporaneidade. Se analisarmos a situação da prática educativa dos anos 80 até
a atualidade identificaremos problemas como: a grande ênfase dada à memorização
e pouca preocupação com o desenvolvimento do pensamento matemático para a
reflexão crítica e autocrítica do conhecimento que apreende. (PAVANELLO, 2003)
Em conformidade com a retrospectiva histórica publicada por Falvetta
(2002), a Matemática entrou na escola no final do século XVIII, com a forte influência
da filosofia positivista de Auguste Comte, cuja fundamentação teórica se
demonstrava herdeira fiel à teoria do método de René Descartes. Até então as
ciências eram reservadas aos grandes filósofos. Os estudos históricos sobre a
constituição das disciplinas do ensino científico praticamente inexistiram, porém
alguns mostram que os primeiros textos para a escolarização da matemática no
Brasil, surgem nas primeiras décadas deste mesmo século. Enquanto isso se sabe
da história que, nas escolas européias o livro didático era o Elementos de Euclides
e a comunidade de filósofos e estudiosos da época dominava o conhecimento
histórico e filosófico construído até então. Além disso, a imprensa faz a transição do
manuscrito para o impresso, ampliando as condições de acesso e de produção do
conhecimento. No século seguinte, Hilbert faz uma releitura de Euclides e imprime
um caráter mais abstrato à obra do matemático grego. Com isso, o ensino da
matemática assume as características dessa época. Se estudarmos os trabalhos de
Euclides observa-se que
ele
elimina
da
matemática
os procedimentos
experimentais e cria uma mediação de leitura do real através dos elementos
geométricos e suas propriedades e, ao contrário, se estudarmos Hilbert constata-se
que ele elimina as figuras geométricas e estabelece a axiomática na geometria. O
formalismo se instalou no ensino da matemática que caracterizou o ensino
tradicional. A releitura que Hilbert fez de Euclides aperfeiçoou o dedutivo e penetrou
o ensino de matemática de modo geral. O enfoque formal se impõe na ciência e
adentra no seu ensino.
A mesmo autor ainda complementa que a especialização das ferramentas
cria condição para o surgimento da máquina como combinação de ferramentas
simples. Com estas bases a expansão do comércio gera novas instituições
financeiras e a necessidade de mão de obra qualificada. A produção mecanizada
lentamente elimina o artesanato e o sistema doméstico de produção. A Revolução
Industrial, a administração e os sistemas bancários de produção passaram a exigir
mais do cidadão. A matemática chega às escolas para preparar este cidadão que o
mercado exige. Entretanto, o currículo e os livros didáticos são criados com base no
raciocínio dedutivo do grego Euclides (século III a.C.). Tal procedimento mostra-se
importante para a compreensão da matemática , mas não para o Ensino Básico,
por não estar adequado às necessidades sociais e às possibilidades intelectuais da
grande maioria das pessoas que buscavam conhecimentos sistematizados. No
século XX, durante as guerras mundiais, a matemática evolui e adquire importância
fundamental nas escolas. Contudo, a concepção formalista continua resistindo e se
impondo. Novas propostas educativas matemáticas vão surgindo nos meios
escolares, porém se esvaíram diante da impregnação do formalismo clássico. A
partir dos anos 70 começa a disseminação de escolas de Educação Básica, isto é, a
população passa ter oportunidade de acesso aos saberes sistematizado pela
humanidade.
Ainda conforme Falvetta (2002), no período pós-guerra os norteamericanos, a fim de formar cientistas e superar os avanços soviéticos, fazem da
matemática um conjunto de algoritmos e desvalorizam a elaboração conceitual,
marcando o início da efetivação do Movimento da Matemática Moderna (MMM), na
década de 70. Parecia uma ótima idéia, porém mal encaminhada, pois está apoiada
na teoria dos conjuntos, com desprezo à resolução de problemas aos aspectos
históricos, com primazia aos conteúdos aritméticos e algébricos e uma certa aversão
a geometria. A ênfase aos aspectos estruturais e à precisão de sua linguagem
caracteriza a matemática moderna como eminentemente formal, ou seja, não
priorizando a significação dos conceitos matemáticos. Segundo Pavanello (2003), os
símbolos e suas relações não ampliaram o conhecimento inicial do
contrário,
reforçaram
a
memorização
do
mesmo para
aluno;
ao
realizar operações
lógicas. É muita técnica operatória para o estudante do ensino fundamental e pouca
preocupação com a capacidade de pensar dos estudantes. Neste sentido, o efeito
maléfico de um ensino sem significações seria determinante para uma enxurrada de
alunos reprovados e com dificuldades de aprendizagem no Ensino Médio.
(PAVANELLO, 2003)
Foram as próprias exigências vindas da sociedade que começaram a impor
uma certa mudança nessa visão funcionalista da educação. Os avanços
tecnológicos e a expansão econômica dos anos 60, propiciaram o
surgimento de pressões para que a escola tivesse os interesses voltados
para as necessidades do capital. Houve, então, um deslocamento da ênfase
no papel da educação. Privilegiando as exigências de uma sociedade
tecnocrática, o sistema educacional passou a adotar preocupações com a
qualificação técnica e profissional visando a formação de quadros, bem
como com a mobilidade da mão-de-obra. O que estava em jogo, pois, nessa
visão funcional-tecnocrática da educação era a adaptação ás exigências do
mercado. (MOISÉS,1997, p.13)
As críticas ao ensino da matemática se acirraram. Com isso, começa o
Movimento de Educação Matemática, no Brasil, início dos anos 80, surgindo grupos
de estudo e pesquisa. É neste contexto que o ensino da Matemática tem uma
aproximação com a psicopedagogia, com a Filosofia e a Sociologia, pois a
preocupação dos especialistas e professores era
com a elaboração do
conhecimento, por parte dos estudantes. (PAVANELLO, 2003)
Moisés, em Aplicações de Vygotski na Educação Matemática (1997),
afirma que embora no campo da Educação Matemática se debatam novas propostas
para um ensino de Matemática que proporcione realmente seu aprendizado, nos
cursos de formação de professores, uma quantidade enorme de informações é ainda
despejada
sobre
os
estudantes
como se os mesmos fossem seres
desprivilegiados de raciocínio e capacidade de pensar.
O trabalho nuclear da filosofia da educação matemática é analisar
criticamente os pressupostos ou idéias centrais que articulam a pesquisa e
o currículo ou a proposta pedagógica, buscando esclarecer suas afirmações
e a consonância entre os procedimentos utilizados e as considerações
éticas, epistemológicas e científicas sobre possíveis desdobramentos em
ações pedagógicas e entre as ações visualizadas, ou seja, há consistência
entre a concepção de educação, de ensino, de aprendizagem, de conteúdo
matemático, atividades propostas e desenvolvidas, avaliação proposta e
efetuada na realidade escolar ou educacional? (BICUDO e GARNICA,
2003, p. 21 22)
Sendo assim, verificamos que é correto definir Filosofia da Educação
Matemática como a procura das razões, das conseqüências e do sentido da
educação Matemática no processo educativo. É o questionamento radical da
imagem de homem que se pretende obter e ainda mais, é a investigação dos
pressupostos, dos condicionamentos e dos objetivos de se ensinar Matemática.
Neste sentido, o conhecimento em Filosofia da Educação Matemática e as reflexões
com relação à educação matemática que dela se originam, podem ser
determinantes na metodologia e na prática pedagógica do educador, pois estes
demonstram qual a concepção de matemática, de ensino e de educação que o
profissional tem e, conseqüentemente, determinará os saberes e a aceitação desta
disciplina por parte dos educandos. (BICUDO, 2003)
Caraça, em Conceitos Fundamentais da Matemática, (1998), expõe
claramente duas atitudes em face a ciência, afirmando que a mesma pode ser
compreendida em dois aspectos diferentes. Ou se olha para ela como vem exposta
nos livros de ensino, como coisa criada, onde os capítulos se encadeiam em ordem
e sem contradições, ou se procura acompanha-la no seu desenvolvimento
progressivo,
permitindo-se
assistir
a
maneira
como
foi
sendo
elaborada,
descobrindo-se hesitações, dúvidas, contradições, que só um longo trabalho de
reflexão e apuramento consegue eliminar, para que logo surjam outras
perplexidades, outras dúvidas, outras contradições. No primeiro aspecto, a ciência
parece bastar-se a si própria; no segundo, ao contrário, vê-se toda a influência que a
vida social exerce sobre a sua criação, compreendendo-a como um organismo vivo,
impregnado de condição humana.
Segundo a Proposta Curricular de Santa Catarina (1998), o ensino da
Matemática não se baseia somente em cálculos, mas em uma realidade
ampla e rica que visa não só formar alunos, mas seres humanos comprometidos
com a vida, agentes da história, construtores de uma nova sociedade. Visa à
educação plena do aluno, a formação de valores fundamentais através da busca do
metafísico e da descoberta do sentido mais profundo da existência da Matemática.
Neste sentido, verificamos que o ensino da matemática carece de
mudanças. A realidade nos mostra a necessidade e a urgência que na formação de
professores, além do domínio nas áreas de conhecimento se dê também prioridade
ao desenvolvimento de atitudes que permitam não só aceitar a mudança e a
inovação, mas ser ele próprio agente de mudança, através de práticas de reflexão.
(SCHEIBE & DAROS, 2002)
A Filosofia da Educação Matemática tem apontado que tendências se
apresentam para prática pedagógica e que nelas se explicitam os modos de
conceber a Matemática, seu ensino e sua aprendizagem.
Tais tendências, como afirma Fiorentini (1995), historicamente, surgem
com a preocupação de melhorar a qualidade do ensino da Matemática .
No entanto, temos convivido com informações e dados da literatura que
indicam o estado nada alentador e apontando a prática docente dos professores
reprodutivistas como responsável.
Os dados até aqui mencionados conduziram-nos a formulação do
seguinte questionamento: "Qual é o entendimentos que os professores de
matemática do ensino fundamental e médio, da E.E.B.J.D., apresentam com relação
à formação de professores tendo como base as diversas concepções de Filosofia da
Educação Matemática?
Neste sentido, outras questões se desdobraram:
Que concepções de ensino de matemática transitam no cotidiano escolar?
Quais as determinações que levam os professores terem este entendimento?
É possível ensinar matemática sem a repetição exagerada de exercícios que,
segundo alguns formalistas, oportunizam o domínio da técnica?
Levando
em
consideração
os
questionamentos
apresentados
anteriormente acreditamos que não podíamos apresentar objetivos diferentes aos
expostos a seguir, quando analisamos:
As concepções que os educadores têm com relação ao ensino e a Filosofia
da Educação Matemática;
A organização do processo ensino aprendizagem como estabelecimento de
relações
para
os condicionantes
uma
nova
prática
sociais, históricos
pedagógica,
e
políticos
conseguem
que
indicar
contribuíram
para aprodução dos conceitos matemáticos e o conteúdo trabalhado;
As perspectivas do ensino da Matemática a partir da ação docente.
Partindo do principio que a aprendizagem se constitui num processo social
e que o indivíduo deve se apropriar das significações dos conceitos e não apenas
memorizá-los, (Proposta Curricular de Santa Catarina;1998), não é difícil perceber
que o processo de ensino-aprendizagem apresenta-se muito desgastado, uma vez
que é baseado na transmissão de explicações descontextualizadas e nos exercícios
repetitivos, o que vem a ser uma ação equivocada, já que os professores ao
trabalharem os conteúdos priorizam a memorização desprezando, desta forma, as
significações dos conceitos matemáticos.
Gadotti, (1995), salienta a importância dos professores saberem que não é
a consciência do homem que determina o seu ser, mas pelo contrário, o ser social
é que determina a sua consciência, logo, manter a tensão dialética entre individuo e
sociedade talvez seja o principio básico de uma pedagogia que pretenda ser
transformadora das condições humanas, de suas relações consigo mesmo e com o
mundo. Sendo assim, relação educativa não se dá entre indivíduos singulares, mas
sempre entre indivíduos que representam o todo complexo social. (MANACORDA,
1996)
Desta forma, para Saviani, (1980), é preciso então, pensar numa
educação que objetive trabalhar o senso comum de modo a extrair o seu núcleo
válido e dar-lhe expressão elaborada com vistas à formulação de uma concepção de
mundo adequada aos interesses populares.
A prática pedagógica deve ter como objeto a socialização do
conhecimento já acumulado historicamente pela humanidade, visando
a que esse conhecimento seja utilizado pelos educandos no processo de
transformação da realidade em que eles vivem. (DUARTE, 1987, p.11)
Segundo Vasconcelos (1998), a Filosofia da Matemática influencia de
forma decisiva no modo como ensinamos e reflete logicamente no modo como os
nossos alunos aprendem Matemática. Constatamos então que, a prática pedagógica
destes professores é a responsável pela organização das experiências da
aprendizagem dos alunos. O que os mesmos fazem na sala de aula é em função do
que pensam sobre a Matemática e como sentem a Matemática e o seu ensino
O tempo exige um novo paradigma para formação de licenciados: Um
licenciado novo
portador de uma nova missão, capaz de entender a
globalização que se instaura, tecnicamente capaz de utilizar/lidar com a
informação em todos os níveis, de problematizar e analisar
conjunturalmente o que está a sua volta para, com o seu aluno, responder
aos desafios de uma nova era, ou de um novo momento histórico. (FROTA,
2003, p.127)
De acordo com Biccudo e Garnica, (2003), a filosofia da educação
matemática é constituída por aspectos, da filosofia, da filosofia da educação e da
filosofia da matemática, porém se revela numa área própria de indagação e de
procedimentos. Diante do exposto, achamos conveniente destinar o capítulo 2 para
melhor esclarecermos cada área de inquérito em questão.
Com base em alguns comentários que expomos até aqui sobre Filosofia
da Educação Matemática e seu arcabouço de significados, verificamos que não há
prática pedagógica que não seja influenciada por uma concepção filosófica sobre a
natureza desta ciência.
É neste contexto começamos a nossa pesquisa.
Inicialmente, estabelecemos contato com a direção e as professoras de
Matemática do Ensino Fundamental e Ensino Médio da E.E.B.J.D., situada no bairro
Quarta Linha município de Criciúma. É importante salientar que os dados coletados
para o desenvolvimento deste trabalho foram obtidos através de conversas
informais, (sala dos professores), e dos acompanhamentos durante as aulas com as
respectivas professoras.
Para que pudéssemos analisar os dados obtidos, resultantes das
observações feitas nas aulas que mencionamos acima, efetuamos uma série de
leituras referente ao objeto pesquisado, com o intuito de adquirirmos fundamentação
teórica adequada, objetivando compreender e analisar tais informações com maior
aproximação possível para que pudéssemos identificar as perspectivas do ensino da
Matemática a partir da ação docente e quais concepções que as educadoras têm
com relação ao ensino e a Filosofia da Educação Matemática.
É importante salientar que estas informações foram evidenciadas na
prática pedagógica e na metodologia utilizada pelas professoras em sala de aula,
desta forma, destinamos o capitulo 3, intitulado:
Aulas de Matemática: Que
filosofia? para melhor elucidar os dados obtidos/analisados no decorrer do trabalho.
Enfim, com base em alguns comentários que expomos até aqui sobre a Filosofia da
Educação Matemática e seu arcabouço de significados, verificamos que não há
prática pedagógica que não seja influenciada por uma concepção filosófica sobre a
natureza desta ciência.
2 FILOSOFIA DA EDUCAÇÃO MATEMÁTICA
SIGNIFICAÇÕES QUE SERVEM
DE ESCLARECIMENTO PARA UMA FORMA DE PENSAR E CONCEBER A
EDUCAÇÃO MATEMÁTICA -
Antes de iniciarmos a elucidação do nosso objeto de estudo, procuramos
ilustrar o caminho que percorremos pelo pensamento filosófico
da Educação e Filosofia da Matemática
Filosofia, Filosofia
até encontrarmos uma via que nos
remetesse e ao mesmo tempo nos interligasse à Educação Matemática. Nossa
verdadeira intenção é estabelecer relações entre a Filosofia da Matemática e a
Educação Matemática, constituindo, assim, um novo olhar, (Filosofia da Educação
Matemática), que fundamentou a nossa pesquisa: A Filosofia da Educação
Matemática na formação de professores do ensino fundamental e médio.
Para que tal comentário fosse possível, abordamos separadamente,
Filosofia, Filosofia da Educação e Filosofia da Matemática, na tentativa de explicálas e averiguar seus pontos comuns, para que assim se justificasse o termo Filosofia
da Educação Matemática.
2.1 Filosofia
Quando se deu passagem do mundo mítico para a consciência racional,
apareceram os primeiros sábios. A palavra Filosofia surge na Grécia, séc.VI a.C. nos
escritos de Pitágoras, que não querendo definir-se como sábio
SOPHOS
em grego
prefere autodenominar-se Filos-sophos ou seja, amigo do saber ,
aquele que busca a sabedoria. Para ele, esta era uma denominação mais humilde e
fiel à sua postura de tentar compreender a realidade de seu tempo (COTRIM, 1996).
De acordo com Cyrino & Penha (1986), no séc. V a.C. Heráclito define
melhor o conceito original do vocábulo Filosofia: a busca de compreensão da
realidade total , em todas as suas formas, de maneira disciplinada. Opõe-se ao
conceito de polimathéia , ou seja, um saber comum, desconexo, fragmentado, no
nível de senso comum, geralmente preconceituoso e limitado, sobre a realidade
pessoal, social e da natureza.
Podemos observar que a filosofia desde sua definição originária, se faz
compreender como um saber sobre a condição humana pessoal e social, sobre a
cultura, sobre o mundo. Um processo sempre dinâmico de apreensão das
significações históricas da realidade humana de maneira humilde e processual.
Portanto, a filosofia não se trata de um saber abstrato, à margem da vida. O próprio
tecido do seu pensar é a trama dos acontecimentos, é o cotidiano; por isso a filosofia
se encontra no seio da história, enfatizando que não é um corpo de doutrina e nem
um saber acabado referindo-se a um determinado conteúdo, ou seja, não é um
conjunto de conhecimentos estabelecidos de uma vez por todas. (BORNHEIM,
1969)
Segundo Martins & Aranha (1986), nos seus primórdios, a ciência se
achava ligada à filosofia, sendo o filosofo aquele sábio que refletia, sobre todos os
setores da indagação humana. Por isso, é possível falar na teoria de Tales e
Pitágoras e na física e astronomia Aristotélica.
De acordo com as mesmas autoras, partir do século XVII, a revolução
cientifica iniciada por Galileu determinou a ruptura dessas duas formas de
abordagem do real. Lentamente apareceram as chamadas ciências particulares
matemática, física, astronomia, química, biologia, psicologia, sociologia, etc. -,
delimitando campos específicos de pesquisa. Na verdade, o que estava ocorrendo
era o nascimento mesmo da ciência, pois ela não existia propriamente antes disso.
Com este acontecimento, ocorre a fragmentação do saber, cada ciência se
ocupando de um objeto especifico.
Fica, então, a dúvida: o que resta à filosofia se ao longo dos tempos houve
um esvaziamento de seus conteúdos, decorrente do aparecimento das ciências
particulares, tornadas independentes?
Neste sentido, Martins & Aranha, (1986), corroboram com nossa resposta,
quando afirmam que na verdade a filosofia continua tratando desta mesma realidade
apropriada pelas ciências. A diferença é que, as ciências se especializam e
observam recortes do real, enquanto a filosofia jamais renuncia em considerar o
seu objeto do ponto de vista da totalidade. Desta forma, podemos compreender que
a alma da filosofia é uma visão de conjunto, ou seja, o problema tratado nunca é
examinado de modo parcial, mas sempre sob a perspectiva do todo, relacionando
cada aspecto com os outros do contexto em que está inserido. Em todos os setores
da ciência, a filosofia deve estar presente como reflexão crítica a respeito dos
respectivos fundamentos das diversas áreas de conhecimento.
Para Teles (1975), a filosofia propriamente dita tem condições de surgir no
momento em que o ato de pensar é posto em causa, tornando-se objeto de uma
reflexão. Por sua vez, refletir é retomar o próprio pensamento, pensar o já pensado,
voltar para si mesmo e colocar em questão o que já se conhece.
Se pensar o próprio pensamento e colocar em questão o que já se
conhece é refletir, então, podemos compreender a reflexão como o ato de filosofar?
Concordamos com o professor Dermeval Saviani, (1980), ao afirmar que a
reflexão é filosofia quando é radical, rigorosa e de conjunto.
Ou seja:
Radical: (primeira exigência) - exige-se que o problema seja colocado em
termos radicais (...), é preciso que se vá até as raízes da questão, até seus
fundamentos.
Em
outras
palavras,
exige-se
que
se
opere
uma reflexão
em profundidade.
Rigorosa: (segunda exigência) para garantir a primeira exigência, deve-se
proceder com rigor, ou seja, criticamente, segundo métodos determinados,
colocando-se em questão as conclusões da sabedoria popular e as generalizações
que a ciência pode ensejar.
De conjunto: (em terceiro lugar), o problema não pode ser examinado de
modo parcial, mas numa perspectiva de conjunto, relacionando--se o aspecto em
questão com os demais aspectos do contexto em que está inserido. È neste ponto
que a filosofia se distingue da ciência de um modo mais marcante.
Segundo Martins e Aranha (1986), é ela, a filosofia, que: permite o
distanciamento para a avaliação dos fundamentos dos atos humanos e dos fins a
que eles se destinam; reúne o pensamento fragmentado da ciência e o reconstrói na
sua unidade; retoma a ação pulverizada no tempo e procura compreendê-la.
Portanto, a filosofia é a possibilidade da transcendência humana, ou seja,
a capacidade que só o homem tem de superar a sua imanência, (que significa a
situação dada e não escolhida). Pela transcendência, o homem surge como um ser
de projeto, capaz de construir o seu destino, capaz de liberdade. Esta abordagem
dialética da filosofia quer dar ao homem uma consciência crítica de seu tempo. É
uma postura segura, reflete sobre o dogmatismo, permitindo uma compreensão mais
realista das estruturas sociais, retirando o espaço do moralismo, dos reformismos e
formalismos e nos remete para a exigente compreensão dos conflitos estruturais.
Terminam as ilusões de que a realidade seja alimentada por idéias, intenções,
afeições e vontades pessoais. (MARTINS & ARANHA, 1986)
Para Martins & Aranha (1986), o que a filosofia dialética propõe é a
interação entre teoria e prática, o que não acontece no pensamento formal. Desta
forma, o que buscamos é uma mediação para compreender as estruturas do nosso
sentir, pensar e agir. Com a mediação dialética (materialista), somos capazes de
evitar a consciência ingênua, funcionalista, utópica ou idealista.
Sendo assim, a filosofia não faz juízos de realidade, mas juízos de valor. O
filósofo parte da experiência vivida do homem trabalhando numa linha de montagem
repetindo sempre o mesmo gesto, mas vai além desta constatação não só o vê
como é, mas como deveria ser. Julga o valor da ação, sai em busca do significado
dela. Filosofar é dar sentido à experiência. (MARTINS & ARANHA, 1996)
De acordo com Bornheim (1969), a filosofia exige coragem. Filosofar não é
um exercício puramente intelectual. Descobrir a verdade é ter a coragem de
enfrentar as formas estagnadas do poder que tentam manter o status quo, é aceitar
o desafio da mudança. Saber para transformar.
Tudo muda, tudo passa, nada permanece...
(HERÁCLITO, apud, NUNES 1996, p.104)
2.2 Filosofia da Educação
Se a Filosofia da Educação tem alguma coisa a dizer de essencial, de
importante, à educação, é necessário que ela caminhe passo a passo com
a educação, com suas preocupações e suas inquietações, seus problemas.
(GADOTTI 1980, p. 35)
Iniciamos nossas considerações sobre Filosofia da Educação com a
citação de Moacir Gadotti, pois verificamos nela, uma definição simples sobre o ato
de filosofar, mediante as questões que se referem à educação.
De acordo com Saviani (2000), definir filosofia e filosofia da educação não
é uma questão simples, pois a sua multiplicidade conceitual varia de acordo com a
concepção epistemológica defendida pelos diferentes filósofos. Para alguns, a
filosofia deveria se preocupar com a essência, para outros a atenção deveria voltar
se para o fenômeno, uns acreditam que a busca da verdade é a função da filosofia.
Platão considerava a filosofia como o desenvolvimento do saber em benefício do
homem.
Bicudo e Garnica, (2003), afirmam que a Filosofia da Educação, faz uso
das análises e reflexões sobre a educação, a aprendizagem, o ensino, etc..., não os
olhando somente da perspectiva daqueles que estão preocupados com a educação
do outro, mas principalmente com o significado que a mesma assume ao ser
anunciada através de seu ensino e aprendizagem.
Para Bicudo e Garnica (2003), as questões que são cruciais para a
filosofia como: O que existe? , Como se conhece isto que existe? , O que é o
valor? são enfocadas pela filosofia da educação, porém diferenciando-se por
mencioná-las sempre em termos de educação, (neste caso, educação matemática),
ou seja, se a filosofia remete ao pensar analítico, critico e reflexivo, consideramos
correto discorrer que filosofia da educação partilha do mesmo núcleo constitutivo,
ainda que revele características próprias, principalmente no que se refere à
educação. Trata-se da ação de pensar sobre a educação, buscando esclarecer o
seu significado, ou seja, perguntar-se e ir à busca de respostas que justifique o que
é a educação? O que significa ela para o homem, para a sociedade, para a ciência,
arte, religião e estado? Para que educar e com que fim? É possível intervir no curso
dos acontecimentos humanos
históricos e sociais
pela definição e consecução
de metas educacionais? (SAVIANI, 1980). Sendo assim, acredita-se que a filosofia
da educação volta-se para questões que tratam de como se faz educação,
dos aspectos
ensino,
básicos
presentes
ao
ato
educador
como
é o caso do
da aprendizagem, de propostas político-pedagógicas, do local onde a
educação se dá e, de maneira sistemática e abrangente, as analisa buscando
entender seu significado para o mundo e para o próprio homem.
De acordo com Saviani (1980), a tarefa de Filosofia da Educação é de
oferecer aos educadores um método de reflexão que lhes permitam encarar os
problemas educacionais, penetrando na sua complexidade e encaminhando a
solução de questões tais como: conflito entre filosofia de vida e ideologia na
atividade do educador, a relação entre meios e fins da educação, a relação entre
teoria e prática, os condicionamentos da atividade docente, até onde se pode contálos ou superá-los. Neste sentido, o mesmo autor afirma que os educadores precisam
compreender que consciente ou inconscientemente toda prática pedagógica está
embasada numa teoria, numa filosofia, ou seja, numa concepção de mundo, de
educação e de homem que se pretende formar. Esta deveria ser a primeira definição
a ser feita, antes mesmo de se definir quais os objetivos da educação. Sendo assim,
para Saviani, (1980), o modo pelo qual a filosofia da educação procede varia
conforme os pressupostos filosóficos que assume.
Com relação a nossa pesquisa, ousamos afirmar que se fundamenta na
filosofia Marxista
materialismo dialético
e na teoria científica, materialismo
histórico.
Com o intuito de melhor explanar as peculiaridades referentes à Filosofia
da Educação que comunga dos pressupostos da Filosofia Marxista, iremos
considerar as concepções (de filosofia e de filosofia da Educação) de Demerval
Saviani (1980) e (2000) e Moacir Gadotti (1980) e (1995).
Para Saviani (1980) e (2000), podemos conceituar filosofia como uma
reflexão (radical, rigorosa e de conjunto) sobre os problemas que a realidade
apresenta. Sendo assim a Filosofia da Educação não seria outra coisa senão
uma reflexão (radical, rigorosa e de conjunto) sobre os problemas que a realidade
educacional apresenta.
De acordo com Gadotti (1980), a realidade educacional brasileira, nos
remete a contradições, pois ao mesmo tempo em que nossa educação tem sido
pautada pelos princípios do silêncio, da obediência, da passividade, da
dissimulação, (fingir o ensinar e o aprender) da omissão, da exclusão e da
desigualdade, espera-se como resultado dessa prática que o aluno seja um cidadão
crítico, atuante, participativo, honesto, solidário, criativo e humano. É neste contexto
que verificamos a grande contradição se revelando entre o discurso e o fazer
pedagógico.
Gadotti (1995), segue afirmando que a pedagogia do conflito é a teoria de
uma prática pedagógica que procura não esconder o conflito, mas afrontá-lo,
desmascarando-o. Para lutar contra as desigualdades, elas devem estar evidentes
para todos os membros de uma sociedade e não ser percebida como um fato natural
e universal. Os conflitos existem porque os interesses das classes sociais são
divergentes. Uns lutam pela manutenção do
status quo , outros querem a
transformação da estrutura social a fim de que se desenvolva maior igualdade
social. Nesse contexto, o papel do educador deve ser crítico e revolucionário, ou
seja, seu papel é o de inquietar, incomodar, perturbar. O mesmo autor ainda
acrescenta que o educador deve impregnar-se da consciência da contradição. Foi
isso que fizeram, por exemplo, Marx, Nietzsche, Gramsci entre outros grandes
nomes da história.
Libâneo comenta em sua obra Didática (1994),
que o monopólio do
conhecimento é o fator que contribui para a manutenção de uma estrutura social. A
possibilidade para mudança está na apropriação do conhecimento por parte
daqueles que estão à margem da sociedade. É este o princípio que irá reger a
Pedagogia Crítico Social dos Conteúdos, (como menciona na obra), que tem nos
pressupostos filosóficos de Marx, seus fundamentos. De acordo com o pensamento
de Libâneo, é através do domínio de conteúdos científicos, que os alunos poderão
formar consciência crítica face às realidades sociais e assim terão capacidade de
assumir no conjunto das lutas sociais a sua condição de agentes ativos das
transformações da sociedade e de si próprios.
Neste sentido, acreditamos que idéias filosóficas sobre a educação de
Moacir Gadotti, Dermeval Saviani e José Carlos Libâneo, contribuíram de forma
significativa para a formação da concepção da educação como um ato político e
transformador da realidade social.
Conforme Saviani (2000), cabe a filosofia da educação, interrogar os fins
e os meios da ação educadora, colocando a prática educacional do nível do saber
fazer em consonância com aquela do por que e para que fazer deste modo. Para o
mesmo autor, é esse o sentido da prática refletida.
2.3 Filosofia da Matemática
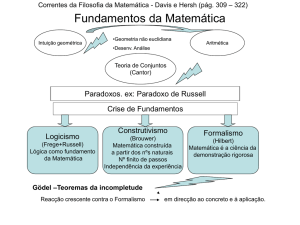
De acordo com Costa (1962), podemos dizer que a preocupação com a
filosofia da matemática constitui a característica que mais claramente marca a
filosofia ocidental das outras grandes tradições filosóficas. O interesse dos filósofos
pela matemática tem várias razões, porém, vamos enfatizar, neste caso, somente
duas (segundo o mesmo autor): em primeiro lugar, a matemática é o exemplo
original de um ramo do conhecimento cujas verdades não estão (ou não parecem
estar) alicerçadas na experiência e em segundo lugar, alguns dos mais profundos
problemas da filosofia encontram a sua formulação mais cristalina quando são
especializados para o domínio da matemática e seus fundamentos.
Segundo o mesmo autor, alguns matemáticos célebres também se
interessaram pelos fundamentos da sua disciplina. Isto foi especialmente verdade
durante o século XIX, quando Russel, Hilbert, Leibiniz, Brouwer, Kant, entre outros,
debateram apaixonadamente os fundamentos da matemática.
Segundo Costa (1962), as tentativas de reformar radicalmente a
Matemática acabaram por gerar as crises dos fundamentos.
De acordo com Davis & Hersh (1986), as crises dos fundamentos são:
A descoberta dos incomensuráveis, século VI aC.:
Por volta do século VI a.C., Pitágoras e seus discípulos descobriram que
nem sempre a cada segmento de reta estaria associado um número natural, ou a
razão entre dois deles que resultaria em um número Q*+.
Os pitagóricos tiveram uma decepção ao aplicarem essas informações ao
triângulo retângulo formado pelos lados e a diagonal de um quadrado de lado 1.
Chegaram a conclusão que a medida da diagonal, que segundo suas concepções
deveria ser um número racional, resultou em um número que elevado ao quadrado
resultava em dois. Os pitagóricos sabiam perfeitamente que aquele número não era
racional.
Mas, preferiram negar a descoberta feita dos números irracionais,
atrasando esta informação ao mundo em no mínimo 2000 anos.
Descoberta das Geometrias não Euclidianas;
No início do séc. XIX, emergiu um ponto de vista audacioso: arquitetar
geometrias autoconsistentes que diferissem da geometria de Euclides, (325 a.C./265
a.C.), em particular no que diz respeito às retas paralelas. As novas teorias
alteraram o centro de interesse da geometria especulativa, transportando-o do
conteúdo para a estrutura, da verdade extrínseca das proposições isoladas para a
coerência interna do sistema total.
Afirmações como esta: A soma dos ângulos internos de um triângulo é
igual a 180º, começavam a ser postas em causa e a merecer alguma atenção.
As
ideias
principais,
destas
novas
teorias,
independentemente por três grandes matemáticos:
foram
concebidas
János Bolay (1802/1860),
Nikolai Lobachevskii (1792/1856) e Gauss (1777/1855).
Introdução dos números Imaginários no Calculo Algébrico;
Ainda sem superar as dificuldades em lidar com os irracionais e os
números inteiros negativos, no século XVI os matemáticos ocidentais começam a se
ver às voltas com os hoje chamados números complexos
até então praticamente
ignorados. Surgidos inicialmente de problemas como achar dois números cuja soma
é 10 e o produto 40 , cuja solução é x1 5
15 e x2 5
15 , faziam jus, na
época, à frase de d Alembert (1717-1783): A álgebra é generosa; muitas vezes
fornece mais do que dela se espera . É que na época os números complexos
careciam de sentido e aplicabilidade.
A rigor sabe-se que a matemática está sempre em crises de fundamentos,
as quais deram início a algumas correntes filosóficas que são:
Logicismo
Formalismo
Intuicionismo
Vamos agora, com o auxilio de alguns autores, (através de suas reflexões
sobre a filosofia e a matemática), que serão citados no decorrer do texto, explanar
um pouco sobre as três correntes filosóficas, seus fundadores e o quais as verdades
matemáticas que defendiam.
2.3.1 Logicismo
Inicialmente, achamos conveniente traçar em linhas gerais a situação
histórica da qual surgiu o logicismo.
Segundo Costa (1962), no começo do século XIX a matemática havia se
desenvolvido muito, porém mostrava-se ainda frágil com relação aos seus
fundamentos, pois os pesquisadores da época preocupavam-se em desenvolver a
ciência tendo em vista somente suas aplicações e não seus alicerces. Verificando,
então, os erros do caminho que vinham seguindo Cauchy, Abel e Weierstrass,
iniciaram o retorno aos fundamentos da matemática com, o intuito de assentar o seu
desenvolvimento em bases sólidas. Tal fato caracterizou um movimento que
culminou com a chamada aritmetização de análise matemática (que engloba
álgebra, aritmética e calculo diferencial), onde paulatinamente foram eliminadas
algumas noções mais confusas como, por exemplo, de infinitésimo, concebida nos
moldes antiquados que estavam na base da análise matemática (fundamentada
unicamente no conceito de número natural).
De acordo com o mesmo autor, de semelhante forma houve renovação
nos fundamentos da geometria e com o advento da geometria não euclidiana,
passou-se a considerar a geometria não como o estudo do espaço real, mas como
estrutura lógica abstrata. Admitindo-se então a existência de várias estruturas
abstratas, concluiu-se que existem diversas geometrias matematicamente possíveis.
Para Costa (1962) todo esse movimento, apresentado aqui de forma
resumida, proporcionou as disciplinas dedutivas atingir um alto grau de perfeição
lógica. Neste sentido, observamos que ao mesmo tempo em que havia a
reestruturação nos fundamentos da matemática, também se processou um grande
progresso na lógica formal.
De acordo com Cotrim (1996), Boole foi o responsável por notável
desenvolvimento quando dotou a lógica de um simbolismo matemático permitindo
análises profundas das operações lógicas. Porém assim estruturada a lógica
apresentava
pouca importância para os fundamentos da matemática. Desta
forma, Peano em 1880, criou uma linguagem lógico-simbólica na qual tratou de
expor todas as disciplinas dedutivas, conseguindo assim, colocar a lógica como forte
contribuinte para a melhor compreensão dos problemas relativos aos fundamentos
da matemática.
Para completar este esboço, não poderíamos deixar de citar Cantor, que a
partir de 1872, começou a publicar trabalhos revolucionários com o intuito de
influenciar não somente nos fundamentos da matemática, mas também nas
concepções referentes a ela. Mencionaremos apenas algumas contribuições de
Cantor com sua obra relativa à Teoria dos Conjuntos. (COSTA, 1962)
Aritmética que engloba números infinitos;
Teoria dos Números Cardinais;
Mostrou como se definir os números infinitos para caracterizar conjuntos
infinitos;
Contribuiu para esclarecer conceitos matemáticos referentes à ordem
dimensão e contínuo.
De acordo com Davis & Herch (1986), mesmo apresentando algumas
teorias que acabaram sendo consideradas paradoxais, Cantor conseguiu incorporar
a Teoria dos Conjuntos definitivamente a matemática.
Em conformidade com o que foi escrito até o momento e ressaltando que
os fatos mencionados até aqui deixaram muitas interrogações, poderíamos afirmar
que a corrente Logicista nasceu ... como coroamento das indagações delineadas
atrás . COSTA (1962, p.11)
Prova disso é que na obra de Bertrand Russel, líder do logicismo,
aparecem as pesquisas de Cantor, Dedekind, Weierstrass, Boole e Peano. Russel
admite que sua tese é como o remate de tais investigações. (RUSSEL, 1974)
Conforme Costa (1971), é importante salientar que antes de Bertrand
Russel, o filósofo alemão Frege, já havia apresentado as teses centrais do
logicismo, porém devido a grande dificuldade de compreensão dos símbolos nela
colocados, a obra ficou praticamente ignorada, até Russel, independentemente
redescobrí-las. Desta forma seria justo e antes disso correto, considerarmos Frege o
precursor do logicismo, não obstante que alguns autores como Quine, apontam
Frege como o verdadeiro fundador da lógica simbólica. (COSTA, 1962)
Russel (1974), afirmou que a tese fundamental do logicismo poderia ser
resumida garantindo que a Matemática reduz-se à lógica, pois mesmo considerando
que historicamente ambas eram consideradas disciplinas distintas, onde a
matemática referia-se a ciência e a lógica ao pensamento, contudo, estas
desenvolveram-se de tal forma que a matemática tornou-se mais lógica e a lógica
mais matemática, ou seja, é impossível traçar divisões entre elas.
Essa assimilação da matemática pela lógica foi o leitmotiv do Logicismo,
uma corrente filosófica de peso da qual Russell é o representante
insigne.(...) Nesse terreno, a Matemática parece possuir um conteúdo
próprio, e é mais freqüente a subsunção da Lógica pela Matemática do que
a inversa, como pretendem os logicistas. Entretanto, resquícios de tal
pretensão podem ser detectados mesmo no senso comum, quando são
associados acriticamente o ensino da matemática com o desenvolvimento
do raciocínio lógico. (MACHADO, 1993, p.36)
De acordo com Chauí (1999), René Descartes introduziu a teoria do
método na ciência, conforme a necessidade que o mesmo apresentava em
organizar o pensamento que segundo ele estava confuso, carecendo desta forma de
organização. Para Descartes, era preciso que se instituísse uma metodologia
(estudo do método), que pudesse conduzir a razão ao conhecimento das coisas
tanto para instruir-se quanto para instruir os outros.(ABBAGNANO, 2000)
Segundo Abbagnano, (2000, p.669)
A Lógica foi interpretada como metodologia na fase póscartesiana.(...)...como a ciência de dirigir a faculdade cognoscitiva no
conhecimento da verdade. (...)...como ciência das operações do intelecto
que servem ´para a avaliação da prova.
Desta forma, podemos compreender que a lógica está intimamente ligada
com a linguagem, que por sua vez pode manifestar-se por símbolos (lógica artificial)
e ser utilizada pelos lógicos através da sintaxe (estudo das relações entre os
símbolos) e a semântica, (estudo dos significados que estes símbolos adquirem ao
relacionarem-se). (CYRINO & PENHA, 1986). Sendo assim, acreditamos que a
lógica visa superar as dificuldades e ambigüidades manifestadas pela linguagem
que devido a sua natureza vaga e metafórica, portanto confusa, (segundo
Descartes), poderia atrapalhar o rigor lógico do raciocínio.
Para Machado (1993, p.35):
Na própria Matemática, atendendo aos pressupostos cartesianos, Newton e
Leibniz, por exemplo, jamais poderiam ter desenvolvido o Cálculo
Diferencial e Intergral, como o fizeram, pois, justamente nesses domínios,
pouco progresso poder-se-ia esperar se se impusesse a classificabilidade
das sentenças em verdadeiras ou falsas como condição de possibilidade de
sua aceitação no arsenal dos resultados aceitáveis.
Neste sentido, verificamos que lógica sempre exercerá atração sobre
muitas mentes, simplesmente porque em um universo onde tanta coisa é incerta, ela
nos oferece maneiras de obtermos certezas com relação à validade ou falsidade das
afirmações. Desta forma, podemos enfatizar que utilizamos a lógica por todo
momento, ou seja, usamos a lógica quando argumentamos e argumentamos quando
tentamos convencer outras pessoas de algo ou quando tentamos nos defender de
alguma acusação que nos é feita. Assim sendo, não é de se estranhar que ao
argumentarmos, fazemos o uso de argumentos que nos permitam provar a verdade
(ou falsidade), que estamos colocando.(MARTINS & ARANHA, 1986)
Mas, qual o significado de um argumento para a lógica?
Primeiramente, vamos definir o termo argumento, com o auxílio de alguns
autores.
Para Abbagnano (2000), argumento é em seu primeiro significado,
qualquer razão, prova, demonstração ou indicio, ou seja, motivo capaz de captar a
aceitação ou de induzir a persuasão ou à convicção. O mesmo autor ainda destaca
que esta palavra foi usada por Frege, como sendo o que preenche um espaço vazio
de uma função ou aquilo a que uma função deve ser aplicada para que tenha
determinado valor.
Segundo Jolivet (1990), um argumento é um conjunto de proposições,
mas não um conjunto qualquer. Num argumento as proposições têm que ter uma
certa relação entre si e é necessário que uma delas seja apresentada como tese, ou
conclusão, e as demais como justificativa da tese, ou premissas para a conclusão.
Normalmente argumentos são utilizados para provar ou desprovar uma proposição
ou para convencer alguém da verdade ou da falsidade de alguma coisa.
Desta forma, para melhor expor o que foi dito por Jolivet no parágrafo
anterior, apontamos um conjunto de proposições, que segundo o autor mencionado,
não é na realidade um argumento:
Todos os bebês choram quando sentem dor.
Todos os anos cada um de nós faz aniversário.
Logo, o CAP é um bom colégio.
Neste caso, observamos que embora todas as proposições sejam (pelo
menos à primeira vista) verdadeiras, e embora elas se disponham numa forma
geralmente
associada com a de um argumento (premissa 1, premissa 2,
e conclusão, precedida por "logo"), não temos um argumento porque as proposições
não têm a menor relação entre si. Não devemos sequer afirmar que temos um
argumento inválido aqui, porque mesmo num argumento inválido as premissas e a
conclusão precisam ter uma certa relação entre si.
Por outro lado, o seguinte conjunto de proposições é um argumento:
Todos os homens são racionais.
Russel é homem.
Logo, Russel é racional.
Neste caso, temos um argumento válido. Nele, todas as premissas são
verdadeiras e a conclusão também (ou, pelo menos, parecem ser), à primeira vista.
Com o auxílio de Cyrino e Penha (1986), Cotrim (1993), Martins & Aranha
(1986), Jolivet (1990), Russel (1974) e Zimbarg (1973), elaboramos alguns exemplos
de argumentos e sua respectivas classificações, de acordo com o modo que se
apresentam.
1º Argumento:
Se você me amasse (p), não teria me deixado sozinha (q).
p
q
~q (você me deixou sozinha)
.
..
~p (logo, você não me ama)
Argumentos como o apresentado são tão comuns que "modus tollens" é o
nome latino dado a argumentos que têm essa forma.
[Forma do Argumento Válido Modus Tollens - Negação do Conseqüente]
Esse argumento, e todos os que possuem a mesma forma, é um
argumento válido. O raciocínio é correto. Resta saber se as premissas usadas,
especialmente
a
primeira,
são
verdadeiras.
Se
forem,
a
conclusão
é,
necessariamente, verdadeira. Se não forem, ou se pelo menos uma delas não for, a
conclusão não precisa ser verdadeira, mesmo que o argumento seja válido, como
este.
2º Argumento:
Se você me ama (p), você não me deixa aqui sozinha (q).
p
q
q (Você não me deixa aqui sozinha)
.
..
p (Logo, você me ama)
A forma desse argumento é a seguinte:
[Forma da Argumento Inválido (Falácia) de Afirmação do Conseqüente]
Todos os argumentos que têm essa forma são inválidos. Mesmo que as
premissas sejam verdadeiras, a conclusão pode ser falsa. Este argumento não
convence muita gente, pois você pode aceitar a premissa que Se você me ama,
você não me deixa aqui sozinha, e admitir que você não deixou ninguém sozinho,
sem aceitar a conclusão.
3º Argumento:
Se você não me deixa aqui sozinha (q), você me ama (p).
p
q
p (Você não me deixa aqui sozinha)
.
..
q (Logo, você me ama)
Este argumento,
"modus ponens":
válido,
tem a seguinte forma, chamada em latim de
[Forma do Argumento Válido Modus Ponens - Afirmação do Antecendente]
4º Argumento:
Se você me deixa aqui sozinha (p), então você não me ama (q).
p
q
~p (Você não me deixa aqui sozinha)
.
..
~q (Logo, você me ama)
Este argumento, inválido, provavelmente não convence ninguém, pois o
fato de não deixar alguém sozinho não quer dizer necessariamente que outro
alguém o ame. Sua forma é a seguinte:
[Forma do Argumento Inválido (Falácia) de Negação do Antecedente]
5º Argumento
Ou você faz o que eu quero (p), ou você não me ama (q)
p
q
~p (Você não faz o que eu quero)
.
..
q (Logo, você não me ama)
Esse argumento é válido e é conhecido como argumento Disjuntivo
Válido.
[Forma do Argumento Disjuntivo - Válido: Negação de um Disjunto]
6º Argumento
Ou você faz o que eu quero (p), ou você não me ama (q)
p (Você faz o que eu quero)
.
..
~ q (Logo, você me ama)
Esse argumento é inválido (Falácia) a forma dele é o Disjuntivo: Afirmação
de um Disjunto.
De acordo com Alencar Filho, (1978), a lógica não está interessada no
processo, e sim no produto: nos argumentos. Na verdade, ela se interessa pelos
princípios que permitem distinguir argumentos válidos dos inválidos. Conforme o que
mencionamos anteriormente, os argumentos são constituídos por proposições, e,
por isso, a lógica se interessa por proposições, enquanto componentes básicos de
argumentos. Em regra, a lógica não se interessa pela verdade ou falsidade das
proposições que compõem um argumento: interessa-se, sim, pelas relações que as
proposições têm umas com as outras, especialmente se o conjunto de proposições
que formam as premissas de um argumento implicam a proposição que é sua
conclusão. (CORBISIER, 1987)
Para Alencar Filho, (1978), embora a lógica não se interesse pela verdade
ou falsidade das proposições que compõem um argumento, quando a verdade ou
falsidade é contingente, ela estipula alguns princípios básicos que estabelecem as
condições básicas em que as noções de verdade e falsidade devem operar.
De acordo com o mesmo autor, os três princípios básicos da lógica são:
1ª - Princípio do Terceiro Excluído verdadeira ou falsa -- não há terceira alternativa
Uma proposição sempre é ou
2ª - Princípio da Não-Contradição - Uma proposição nunca é ambas as
coisas, verdadeira e falsa
3ª - Princípio da Identidade - Se uma proposição é verdadeira, ela é
verdadeira, sempre; se ela é falsa, ela é falsa, sempre.
De acordo com Machado (1993), Russel (1974), Cotrim (1996), Martins &
Aranha (1986), Jovilet (1990) vamos brevemente analisar cada um desses
princípios:
1º Princípio do Terceiro Excluído - O Princípio do Terceiro Excluído
estipula (afirma) que uma proposição é ou verdadeira ou falsa, sempre, sem
exceção. Tem que ser ou uma ou outra coisa, pois não há uma terceira
possibilidade. Por isso é que o princípio se chama "Terceiro Excluído". Em um certo
sentido isso parece até bastante óbvio.
Contudo, Jovilet (1990), Zimbarg ( 1973), Machado (1993) e Russel
(1974)), afirmam que muitos autores ainda têm tentado contestar a verdade desse
princípio, argumentado que as proposições que se referem a estados de coisas ou
eventos futuros não são nem verdadeiras nem falsas, visto que aquilo a que se
referem ainda não ocorreu, e que, portanto, existe uma terceira possibilidade, além
da verdade e da falsidade: a indeterminação.
Contrariando os autores acima citados, Alencar Filho (1978), afirma que
não há proposições simultaneamente verdadeiras e falsas. Por exemplo, na
proposição:
Hoje 18 de outubro faz sol, é dotada de uma verdade, pois é algo
perceptível. Por sua vez, a proposição:
Amanhã, dia 19 de outubro fará sol. Por se tratar de uma proposição de
previsão futura, é válido ou admiti-la como falsa ou verdadeira. No entanto, quando
chegar amanhã e pudermos comprova-la, tal proposição não será a mesma. Pois se
trata de um novo dia, sendo assim, uma nova proposição. Desta forma, as
proposições que os críticos chamam de indeterminadas são proposições,
verdadeiras ou falsas, cuja verdade ou falsidade não é possível determinar no
momento, porém, quando determinadas não se tratam mais da mesma proposição.
2º O Princípio da Contradição - O Princípio da Contradição estipula que
uma proposição nunca é verdadeira e falsa ao mesmo tempo, isto é, que ela não
pode ser ambas as coisas.
De acordo com Cotrim (1996), dois conceitos são contraditórios, quando
não podem não ser e ser ao mesmo tempo, ao analisarmos de um mesmo ponto de
referência. Desta forma o autor cita como exemplo de contradições:
O fracasso é o sucesso.
O circulo é quadrado.
O interior é o exterior.
Segundo Jovilet (1990), a milenar aceitação desse princípio não está
sujeita a ataques, ou seja, se afirmamos que esse princípio é verdadeiro, e outra
pessoa diz que é falso, não é possível que nós dois estejamos certos, ou seja, que
nós dois tenhamos a verdade. Um dos dois tem que estar errado. A própria negação
do princípio implica, portanto, sua aceitação.
3º O Princípio da Identidade
Segundo Cotrim (1996), este princípio formulado desde Parmênides, é de
uma tal evidencia e objetividade que sua formulação chega a ser extravagante. Para
este autor, tudo é idêntico a si próprio, ou seja: O ser é.
Sendo assim, o mesmo autor segue afirmando que o principio da
identidade é tautológico, (tauto = o mesmo). Isto significa que uma proposição pode
ter sujeito e predicado iguais, ou seja, com o mesmo conceito. Por exemplo:
Você é você. (sujeito e predicado com o mesmo conceito)
Conforme afirmam Martins & Aranha (1986), a lógica aristotélica baseia-se
no princípio da identidade, partindo, portanto de uma concepção estática da
realidade, a qual se explicaria por intermédio de noções absolutas, sendo assim, não
é possível a contradição.
2.3.2 Formalismo
Antes de iniciarmos as considerações sobre o formalismo na Matemática,
é oportuno fazer alguns comentários sobre o conceito forma , do ponto de vista da
Lógica Matemática , ou seja, Lógica Simbólica.
Segundo Abbagnano (2003, p.469):
...diz-se habitualmente que a matemática é uma ciência da forma (no
sentido formal), porque o que ela ensina não vale para certos conjuntos de
coisas mais sim para todos os conjuntos possíveis, já que versa sobre
certas relações gerais que constituem o aspecto formal das coisas. Neste
sentido, a palavra forma foi usada pela primeira vez por Tetens, para
indicar as relações estabelecidas pelo pensamento entre as
representações sensíveis, que por sua vez constituíram a matéria do
conhecer.
Para Davis & Hersh (1986), ainda que o sentido mais comum do termo
forma relacione-se com o feitio externo dos objetos materiais, também é costume,
na linguagem trivial, falar de forma em um sentido mais amplo, como por exemplo:
Quando se comenta que uma composição poética está em forma de soneto;
Quando verifica-se que uma composição musical está em forma de sonata.
Para o mesmo autor, o que se pensa nesse momento é nas propriedades
estruturais que podem ser observadas, sem ter em conta o significado dos versos
ou dos motivos que inspiraram a música. Da mesma maneira usa-se o termo
estrutura não só para indicar a composição de um corpo sólido, mas também se
referindo à estrutura de uma sociedade, de um discurso, e assim por diante.
Segundo Manno (s/d), do mesmo modo pode-se pensar em estruturas
lógicas ou formas lógicas, sendo que tais expressões representam um aspecto que
se reveste de fundamental importância: o aspecto formal. A lógica formal é um tipo
de investigação sobre a linguagem e analisando suas estruturas, pode-se perceber
que estas prescindem de conteúdos concretos que posteriormente sejam dados a
estas estruturas (gerando proposições concretas de um discurso falado ou escrito,
como acabamos de mencionar anteriormente durante as reflexões sobre a corrente
Logicista. A forma lógica diz respeito ao raciocínio dedutivo, ou seja, ao conteúdo
das coerências que organizam uma demonstração, prescindindo-se dos conteúdos
semânticos do discurso. A lógica, nesse caso, somente se ocupa do problema do
desenvolvimento dessa demonstração. O fato de prescindir dos conteúdos nos
mostra a possibilidade de utilizar-se estruturas dedutivas mediante símbolos, e isso
permite uma exatidão da análise estrutural que seria muito mais difícil de conseguir
sem o auxílio do simbolismo. (BARKER, 1976)
Para Corbisier (1987, p.104):
A lógica formal é formalista, ou tende fortemente ao formalismo, na medida
em que desinteressando-se do conteúdo, permanece no momento da
abstração que retira ou destaca do real, apenas um de seus aspectos, isto
é, a forma.
De acordo com Costa (1962), Hilbert (analista alemão, criador e principal
representante do formalismo e considerado um dos maiores matemáticos
contemporâneos) não tinha pretensões de reduzir a matemática à lógica,
(diferentemente
dos
matemáticos
da
escola
logicista),
porém,
pretendia
fundamentá-las conjuntamente. Ele e os outros seguidores da escola formalista
viam na matemática a ciência da estrutura dos objetos, sendo que os números são
as propriedades estruturais mais simples desses objetos constituindo-se, desta
forma, também em objetos.
Abbagnano (2003, p.471), define formalismo como:
Toda a doutrina que recorra à forma, em qualquer das significações do
termo.(...). em matemática, foi chamado de formalismo o procedimento que
pretende prescindir dos significados dos símbolos matemáticos,
especialmente a corrente filosófica de Hilbert.
Segundo Barker (1976), o matemático pode estudar as propriedades dos
objetos somente por meio de um sistema apropriado de símbolos, reconhecendo e
relevando os aspectos destituídos de importância dos sinais que utiliza, pois, uma
vez que se tenha um sistema de sinais adequados, não é mais necessário se
preocupar com seus significados, sendo assim, os próprios símbolos possuem as
propriedades estruturais que interessam. Neste sentido, o matemático deve apenas
investigar, segundo os formalistas, as propriedades estruturais dos símbolos, e,
portanto dos objetos, independentemente de seus significados. Assim como na
geometria ou na álgebra, para simplificar e padronizar determinadas questões, são
introduzidos conceitos não reais que são apenas convenções lingüísticas, também
se justifica a introdução, na matemática, de conceitos e princípios sem significado
dos conteúdos.
De acordo com Barker (1976), o que mencionamos anteriormente acabou
sendo um dos pontos chaves da metamatemática de Hilbert. Sendo assim, o filósofo
e matemático procurou estabelecer um método para se construir provas absolutas
de consistência (ausência de contradição) dos sistemas, sem dar por suposta a
consistência de algum outro sistema. Para isso, Hilbert estabeleceu alguns passos a
serem dados.
Sendo assim, nos apoiamos em Barker (1976), Manno (s/d), Costa (1962)
e Davis & Hersh (1986), para destacar alguns passos que Hilbert estabeleceu. São
eles:
1. A completa formalização de um sistema dedutivo. Isto implica tirar todo
significado das expressões existentes dentro do sistema, sendo assim,
estes sistemas devem ser considerados puros sinais vazios .
2. Combinar expressões. (Expressão é o nome que se dá às palavras do
sistema, que por sua vez são compostas de símbolos abstratos, também
chamados alfabeto do sistema.) A forma como se devem combinar
essas expressões deve estar impregnada em um conjunto de regras de
formação e regras de inferências enunciadas com toda precisão, que
especificam como uma expressão pode ser formada ou transformada
em outra. A finalidade deste procedimento é construir um cálculo que
não oculte nada e que somente apresente o que expressamente se
tenha colocado nele.
3. Tomar um número finito de expressões como sendo o conjunto de
axiomas do sistema. A idéia de prova num sistema formal consiste em
começar com um dos axiomas e aplicar uma seqüência finita de
transformações, convertendo o axioma em uma sucessão de novas
expressões, onde cada uma delas ou é um dos axiomas do sistema ou é
derivada deles pela aplicação das regras de formação.
4. Obter a totalidade dos teoremas, e desta forma constituir o que pode
ser provado no sistema. Os axiomas e os teoremas de um sistema
completamente formalizado são portanto sucessões finitas de símbolos
sem significados.
Segundo Costa (1962, p.35):
...o método axiomático encontra aplicação prática em toda a matemática,
constituindo-se hoje, na técnica básica desta ciência. O formalismo em
poucas palavras, deseja transformar o método axiomático, de técnica que
é, na essência mesma da matemática.
Conforme o mesmo autor, o método axiomático não serve somente para
economizar pensamento e sistematizar teorias. Ele constitui um ótimo instrumento
de trabalho e de pesquisa no domínio da matemática. Assim por exemplo, grandes
avanços feitos no séc. XX feitos em álgebra, topologia e em outros ramos da
matemática, encontram-se correlacionados, de modo intimo, com o método
axiomático.
Sendo assim achamos conveniente apontar um exemplo de sistema
formal relacionado a linguagem computacional e da mesma forma um exemplo de
sistema formal utilizado na demonstração de um teorema matemático.
De acordo com Carvalho & Oliveira (1998, p.121), vamos mostrar um
exemplo de sistema formal utilizado na linguagem computacional:
Um sistema formal é uma tupla < ,L,A,R>, onde:
é um alfabeto;
L é um conjunto recursivo em , chamado de linguagem do sistema
formal;
A é um subconjunto recursivo de L, chamado de Axiomas;
R é um conjunto recursivo de relações em L.
Seja um sistema formal, onde o alfabeto, as palavras, os axiomas e as
relações estejam definidos abaixo:
= {+,*}
L = { *}
A = {+,*}
R = {r1,r2}, onde:
r1 = {<x+,x*> | x
*
}
r2 = {{<x+*,x*+> | x
*
}U
*
{<x+**,x*++> | x
{<x*,x++> | x
}U
*
}}
As relações r1 e r2 são binárias, e seus pares ordenados possuem uma lei
de formação bem definida.
Conforme Davis & Hersh (1986), uma axiomática formalizada converte-se,
em resumo, em uma espécie de jogo grafo-mecânico, efetuado com símbolos
destituídos de significado e regulado por meio de regras determinadas. E isso tem
uma valiosa finalidade: revelar com clareza a estrutura e a função, de maneira
análoga a um manual esquemático e de funcionamento de uma máquina. Quando
um sistema está formalizado, tornam-se visíveis às relações lógicas existentes entre
as proposições matemáticas, como se combinam, como permanecem unidas, etc.
Uma página inteira preenchida com os sinais sem significados não afirma nada: é
simplesmente um desenho abstrato que possui determinada estrutura. No entanto é
perfeitamente possível descrever as configurações de um sistema assim
especificado e formular declarações de acordo com as configurações e suas
diversas relações entre si. Hilbert observou que tais declarações pertencem a
metamatemática, isto é, declarações a respeito dos símbolos e expressões
existentes dentro de um sistema matemático formalizado.
Segundo Davis & Hersh (1986, p.169-170):
Um texto formal é uma cadeia de símbolos. Quando manipulada por um
matemático ou por uma máquina, é transformada em uma outra cadeia de
símbolos.tais manipulações de símbolos podem, elas próprias, ser o objeto
de uma teoria matemática. Quando se considera a manipulação como
sendo feita por uma máquina, a teoria é chamada de teoria dos automata
pelos informáticos ou teoria de recursividade pelos lógicos. Quando a
manipulação é considerada como sendo efetuada por um matemático, a
teoria é chamada de teoria da demonstração .
Da mesma forma que procedemos para o sistema formal computacional,
(teoria automata), vamos agora exemplificar um sistema formal na matemática, ou
seja, uma demonstração matemática (teoria da demonstração).
Para Davis & Hersh (1986), nada melhor do que demonstrar o mais
famoso teorema da história da matemática. Estamos nos referindo ao Teorema de
Pitágoras, como ocorre na proposição 47, do livro I dos Elementos de Euclides
(300 aC).
Proposição 47. Nos triângulos retângulos, o quadrado sobre o lado que subentende
o ângulo reto é igual aos quadrados sobre os lados que contêm o ângulo reto.
Seja ABC um triângulo retângulo que tem o ângulo BAC reto;
Afirmo que o quadrado sobre BC é igual aos quadrados sobre BA, AC.
Pois tracemos sobre BC o .quadrado BDEC, e sobre BA, AC, os
quadrados GB, HC; [I,46] por A, seja AL paralela a 'BD ou CE e unamos AD, FC.
Então, como cada um dos ângulos BAC, BAG é reto, seguese que as
retas AC, AG, passando por A, e de lados distintos de BA, formam corri BA ângulos
iguais a retos, e, portanto, estão em linha reta, isto é, CA está em linha reta com
AG. [1,46]
Pela mesma razão BA está também em linha reta com AH. E como o
ângulo DBC é igual ao ângulo FBA, pois cada um deles é reto: seja o ângulo ABC
adicionado a cada um; portanto, todo o ângulo DBA é igual ao ângulo FBC. [N.C. 2]
E, como DB é igual a BC, e FB a BA, os dois lados AB, BD são iguais aos
dois lados FB, BC respectivamente, e o ângulo ABD é igual ao ângulo FBC:
portanto, a base AD é igual à base FC, e o triângulo ABD é igual ao triângulo FBC.
[1,4]
Ora, o paralelogramo BL é o dobro do triângulo ABD, pois têm a mesma
base BD e estão sobre as mesmas paralelas BD, AL. [I, 41]
E o 'quadrado GB é o dobro do triângulo FBC, pois mais uma vez têm a
mesma base FB e estão sobre as mesmas paralelas FB, GC. [I, 41]
[Mas os dobros de iguais são iguais entre si].
Portanto, o paralelogramo BL é também igual ao quadrado GB.
Semelhantemente, se AE, BK foram unidos, pode-se também demonstrar
que o paralelogramo CL é igual ao quadrado HC; portanto, todo o quadrado BDEC é
igual aos dois quadrados GB, HC. [N.C. 2].
E o quadrado BDEC está descrito sobre BC, e os quadrados GB, HC
sobre BA, AC.
Portanto, o quadrado sobre o lado BC é igual aos quadrados sobre os
lados BA, AC.
Segundo Fiorentini (1995), o que mencionamos até o momento sobre o
formalismo, inclusive nas demonstrações do sistema formal computacional e do
teorema de Pitágoras, tem raízes fortemente marcadas no formalismo clássico que
predominou o ensino, no Brasil, até os anos 50.
De acordo com o mesmo autor, as principais características do formalismo
clássico no ensino da matemática são:
1. O ensino da Aritmética e da Álgebra é baseado em teorias constituídas
de regras prontas, demonstrações, como o exemplo que colocamos
acima, deduções de fórmulas e a busca de teoremas e axiomas para
fundamentar o conteúdo trabalhado, em Geometria; as verdades são
logicamente organizadas.
2. Ênfase no aspecto computacional, visto que a finalidade do ensino
pautava-se em desenvolver habilidades computacionais, bem como o
desenvolvimento do pensamento lógico dedutivo; sendo assim, o
processo ensino-aprendizagem
se resumia em transmissão
e
memorização dos conteúdos;
3. O importante é a teoria, as significações e aplicações, ficam em
segundo plano;
Conforme com as características mencionadas, verificamos que a
corrente formalista clássica é a-histórica e estática, compreendendo a ensino da
matemática como transmissão de uma saber pronto e acabado.
Se,
anteriormente
apresentamos
uma
demonstração
com
bases
marcadas na tendência formalista clássica, acreditamos que seria conveniente
apresentarmos um exemplo de demonstração matemática pautada na tendência
formalista moderna que se manifestou no Brasil por volta dos anos 60/70. Sendo
assim, recorremos novamente, a Davis & Hersh (1996), para representar tal
tendência com os axiomas de Zernelo-Fraenkel-Skolem- (teoria dos conjuntos):
De acordo com Fiorentini (1995), o uso de axiomas e símbolos
matemáticos com ênfase na teoria dos conjuntos é uma das maiores características
do formalismo moderno. Entre esta característica citada por Firentini (1995),
destacamos:
1. Sistema logicamente estruturado e unificado pela teoria dos conjuntos;
2. Fortemente
axiomatizada,
dando
assim,
ênfase
aos
aspectos
estruturais e lingüísticos que fundamentam a matemática.
3. O processo ensino-aprendizagem se resumia em transmissão e
memorização dos conteúdos;
4. O processo ensino aprendizagem era baseado na transmissão e
assimilação da linguagem e dos processos de sistematização e
estruturação lógica da matemática.
Segundo Pavanello (2003), um dos problemas que encontramos no
processo ensino aprendizagem da matemática, é o formalismo. O formalismo
consiste em repetir fórmulas vazias nas aulas, que os estudantes copiam
diligentemente para os cadernos, decorando-as na véspera dos exames.
Para Vianna (1995), o formalismo se encarrega de desunir a historicidade
do processo ensino aprendizagem da matemática, uma vez que, para os
formalistas, não há historicidade para ser abordada no desenvolvimento dos
conceitos. Neste sentido o formalismo é considerado o suporte da filosofia
positivista.
2.3.3 Intuicionismo
Deus nos deu os números naturais, o resto, é obra dos homens...
(KRONEKER, apud Costa, 1962,p.21)
Começamos nossas reflexões e apontamentos sobre a corrente filosófica
do intuicionismo com a fala de Kroneker, pois, entendemos que é a melhor maneira
de caracterizar o pensamento dos filósofos matemáticos que defendem a corrente
Começamos nossas reflexões e apontamentos sobre a corrente filosófica do
intuicionismo com a fala de Kroneker, pois, entendemos que é a melhor maneira de
caracterizar o pensamento dos filósofos matemáticos que defendem a corrente
intuicionista.
Segundo Costa (1962), Kroneker com tal afirmação, queria na verdade,
mencionar que em matemática, tudo deve ser intuitivo e efetivamente construído
pelo matemático (partindo dos números naturais, tidos como claros e intuitivos),
sendo que tal edificação significa a uma ação livre da mente. Sendo assim, o
intuicionismo na filosofia da matemática, significa uma abordagem matemática de
acordo com a atividade mental construtiva dos humanos. Ou seja, qualquer objeto
matemático é considerado um produto da construção da mente humana e, portanto,
a existência de um objeto é equivalente à possibilidade de sua construção.
Para Costa (1971, p. 156):
...a intuição é uma faculdade da mente que conhece imediatamente; isto é,
a intuição não depende de qualquer meio para fazer o conhecimento. Em
particular, a intuição é independente da razão e da linguagem, (estes
elementos passam a ser somente uma ajuda a memória. O resultado da
atividade construtiva da mente, porém é conhecido absolutamente certo e
evidente (porque construído).
Segundo Abbagnano (2003), o termo intuicionismo é utilizado para indicar
atitudes filosóficas ou científicas diversas, que tem em comum o uso da intuição no
sentido mais geral do termo. Neste caso, a relação imediata com um objeto
qualquer, sendo assim considerada por Descartes, como o caminho que leva ao
conhecimento. Todavia, quando Abbagnano se reporta a corrente filosófica da
matemática, o referido autor faz a seguinte afirmação:
...corrente matemática fundada por L.E.J.Brower, inspirada nas idéias de L.
Kroneker (...), ...as teses típicas do intuicionismo de Brower são as
seguintes: 1º a existência dos objetos matemáticos é definida pela sua
possibilidade de construção(...);2º o principio da terceiro excluído não é
válido(...); 3º as definições impredicativas não são válidas. (ABBAGNANO,
2003, p.583)
De acordo com Costa (1962), alguns matemáticos, como Poincaré e Weyl,
comungaram das mesmas teses de Kroneker, porém mostraram-se menos radicais.
Contudo, Brower, um geômatra holandês, resolveu levar as teses de Kroneker ao
extremo, elaborando desta forma uma nova corrente filosófica na matemática
conhecida como intuicionismo.
De acordo com o mesmo autor, Brouwer insiste que a matemática não se
compõe de verdades eternas, semelhantes às idéias platônicas. Opondo-se, ele
procura demonstrar que o saber matemático escapa a toda e qualquer
caracterização simbólica e se forma em etapas sucessivas que não podem ser
conhecidas de antemão. A matemática, em resumo, pertence à categoria das
atividades sócio-biológicas e se destina a satisfazer certas exigências vitais do
homem. Esta atividade pode ser prolongada, mas é pura ilusão querer sintetizá-la
em grupo de fórmulas previamente estabelecidas, como pretendem os logicistas e
os formalistas, aos quais Brouwer se opõe fortemente.
De acordo com os
intuicionistas, o matemático não descobre as entidades matemáticas, pois é ele
próprio quem cria as entidades que estuda. O matemático intuicionista, enquanto
matemático, não se oporá a qualquer filosofia que sustente que o espírito humano,
em sua atividade criadora, reproduza os seres de um mundo transcendente, mas
considerará semelhante doutrina como excessivamente especulativa para servir de
fundamentos a matemática pura. Sendo assim, a matemática, de acordo com o
intuicionismo, originou-se, historicamente, da experiência, através dos sentidos.
Conforme afirma Körner (1985), os intuicionistas acreditam que a
matemática é uma atividade totalmente autônoma e auto-suficiente. Em decorrência
disto, os filósofos do intuicionismo, não aceitam como válidas certas demonstrações
que tem por objetivo provar a
veracidade
dos
objetos
matemáticos
(características de outras correntes filosóficas). Sendo assim, Brower defende que
os juízos matemáticos são sintéticos, pois é uma construção livre e criativa do
espírito humano, e a priori, porque consiste de intuições puras, isto é, intuições
destituídas de todo o conteúdo sensorial. Em resumo, a intuição matemática
estrutura o material empírico. Ao elaborar desta forma a questão da veracidade
matemática coloca-se como um problema interno seu e não como decorrência de
sua relação com o mundo exterior. Tal concepção nos remete a Kant, ao procurar
justificar as leis matemáticas recorrendo ao espaço e tempo como formas de intuição
pura.
Desta forma, nos apoiamos em Machado (1985), para exemplificar o que
mencionamos no parágrafo anterior:
Exemplo: É comum, principalmente em matemática, deduzirmos através
do raciocínio que um número y existe, e desta forma, sua não existência
implicaria em uma contradição. De acordo com o principio do terceiro
excluído, poderíamos então concluir que y existe, já que não temos uma
terceira alternativa. Porém, como a afirmação de que y existe, para
Kroneker significa que o mesmo foi construído, a demonstração
considerada anteriormente não significa nada.
Corbisier (1987), ainda afirma que a intuição é um bom instrumento que
pode ser utilizado para obter, a partir da observação, possíveis interpretações dos
fatos. Enfatiza que a mesma representa um conhecimento imediato, direto da
realidade, acreditando-se, então, que o percebido é verdade, sem fazer uso de
análises prévias. Contudo, o mesmo autor salienta que deve-se ter cuidado, pois
muitas vezes a intuição pode enganar.
Confirmando o que foi mencionado, Soares (1995, p. 65) completa:
Intuições são aquelas idéias que parecem tão evidentes que são aceitas
como verdadeiras, sem questionamentos. Por exemplo, Euclides apresenta,
em Os Elementos, livro 1, em seguida às definições e postulados, algumas
noções comuns (intuitivas!). Uma delas diz: O todo é maior que a parte .
Essa noção comum é uma proposição intuitiva que foi aceita como
verdadeira até o século XIX.
Neste sentido, tomamos como exemplo os apontamentos de Soares
(1995) para ilustrar o que foi mencionado por Corbisier:
Exemplo: Considere a soma S de infinitas parcelas: 1+2+3+4+5.....= S,
como esperamos, certamente a soma S cresça indefinidamente e nesse
caso é exatamente isso que ocorre.
Consideremos agora, admitimos a soma R =
1 1 1 1 1
+ + + + +...
2 4 8 16 32
Intuitivamente, espera-se o mesmo comportamento da soma S para a
soma R. Porém, a soma R resulta em 1. Isto pode ser verificado em parte, com o
uso de uma calculadora, aumentando-se suficientemente o número de parcelas.
Para Manno (s/d), a intuição matemática consiste nas representações dos
objetos matemáticos. Tais representações, são formadas com base em situações
empíricas. Como estas contêm apenas processos e grandezas finitas, é natural que
a maioria das intuições no contexto infinito seja enganosa. Isso ocorre porque o
primeiro juízo dado sobre uma idéia é baseado no que é conhecido e naquilo que já
se tem experiência.
O mesmo poderá, acontecer com alunos acostumados a efetuarem
multiplicações entre números naturais.
S=5x5
S = 25
A tendência do resultado desta operação, obviamente,
é aumentar.
Sendo assim, o resultado será maior que os números que se multiplicam.
Contudo, ao solicitarmos que multipliquem números racionais ou decimais,
1 1
1
x
=
2 2
4
ou
0,5 x 0,5 = 0,25
verificamos que estes mesmos alunos esperam que o resultado continue
aumentando, porém a resposta apresentada é um número menor do que as parcelas
multiplicadas.
Baseando-se, então no que foi mencionado por Corbisier (1987), Soares
(1995) e Manno (s/d), constatamos que mais uma vez, e de acordo com o que
ocorreu no exemplo anterior, o pensamento intuitivo driblou os alunos.
De acordo com Machado (1993), Brower afirma que a matemática é pura,
independente da linguagem especial (lógica) e do formalismo
mesmo admitindo
que ambos são meros acessórios resultantes de uma atividade autônoma. Desta
forma, não admitia em hipótese alguma que um sistema axiomático fosse um
instrumento utilizado com a finalidade de transmitir conhecimento. Portanto o
conhecimento matemático deveria girar em torno de atividades que conduzissem os
alunos a fazerem suas próprias construções
Para Costa (1962), a crítica intuicionista com relação à matemática
tradicional, tão destrutiva e severa, obrigou os filósofos de outras correntes
filosóficas, menos radicais, a desenvolverem métodos novos, na esperança de
reabilitarem as teorias clássicas. Um bom exemplo disso é a corrente formalista, que
progrediu grandemente motivada pelas polêmicas com o intuicionismo.
Segundo Corbisier (1987), a concepção brouweriana quase torna
impossível considerar a matemática como ciência, pois insistia demasiadamente nos
caracteres intuitivo e construtivo das indagações matemáticas, bem como no papel
secundário da linguagem e do simbolismo em geral. Assim, o intuicionismo
transforma essas indagações em atividades estritamente individuais. Levando-se a
tese intuicionista ao pé da letra, chega-se à conclusão de que, surpreendentemente,
cada pessoa tem sua própria matemática (COSTA, 1962).
De acordo com Soares (1995), a intuição é um ponto de partida para o
acesso à realidade. No entanto, é desejável fazer uso do raciocínio dedutivo (da
formalização), para fundamentar e complementar as conclusões de um pensamento
intuitivo. Prova disso, é que muitas teorias, como por exemplo, a geometria
euclidiana, tiveram seu ponto de partida em conceitos intuitivos.
Descartes (apud, SOARES, 1995, p.66), em O Discurso do Método,
estabelece alguns preceitos metodológicos e dentre estes, afirma que, a intuição,
unida ao método dedutivo, serve de critério universal para estabelecer ou não a
evidência de um fato. Diz ele:
O primeiro (preceito) era de jamais receber alguma coisa por verdadeira se
eu não a conhecesse evidentemente ser tal; isto é, de evitar
cuidadosamente a precipitação e a prevenção, e de não compreender nada
a mais em meus juízos do que se apresentasse tão clara e tão
distintamente a meu espírito que eu não tivesse ocasião alguma de o pôr
em dúvida.
Na verdade, Descartes propõe o uso de um método, cujo mecanismo
assegura o emprego adequando da razão, aliando duas importantes atividades
intelectuais: a intuição e a dedução. (SOARES, 1995)
Para Körner (1985) e Machado (1985), freqüentemente nos deparamos
com o desejo de combinar as intenções intuicionistas, com a precisão formalista. No
entanto, uma das conseqüências desta mútua interação é que a nítida divisão dos
matemáticos
e filósofos em logicistas, formalistas e intuicionistas, tende a
perder muito do seu valor e tornar-se mais um artifício pedagógico.
Com relação ao pensamento de Körner (1985), Machado (1985) e Soares
(1995), afirma que é desejável estabelecer uma compreensão intuitiva dos conceitos
antes de expor a definição formal destes. Com isso, possibilita-se ao aluno que
deixe seu raciocínio fluir, completando-o com o raciocínio dedutivo. Desta forma, é
possível dizer que as idéias intuitivas formam a etapa inicial do raciocínio. Isto posto,
é fundamental estar atento para o fato de que, numa primeira etapa, as idéias
intuitivas devem ser submetidas ao processo de formalização, que é o caminho para
se decidir sobre o grau de veracidade da intuição, dentro do contexto em que ela é
considerada. Ou seja, é fundamental estabelecer e formular, juntamente com os
princípios próprios da teoria à qual a intuição fornece de algum modo a matéria
inicial, os princípios formais pelos quais será explorado esse fornecimento inicial.
Desse modo, a formalização, mesmo parecendo apenas um jogo, enquanto age de
acordo com determinadas regras, é um bom método para desvendar as instituições.
O uso da intuição é verificado no trabalho de Bassanezi (1994), ao utilizar
do raciocínio indutivo, para chegar a um modelo matemático que justificasse a
distância necessária e exigida no momento do plantio, entre os pés de batatas.
Tal idéia é compartilhada por Cardoso (anotações durante as aulas de
análise matemática no curso de especialização), quando diz que o princípio da
indução matemática pode nos auxiliar na procura do modelo matemático que
representa, por exemplo, a soma dos n primeiros números ímpares:
Os números ímpares formam a relação:
1 + 3 + 5 + 7 + 9 .... = ?
Onde: a1 = 1
an = 2n
Sn = (a1 + an) . n
1
Sn = ( 1 + 2n
2
1).n
Sn = 2n2
2
Sn = n2
2
Segundo Davis & Hersh, a matemática intuicionista corresponde à
categoria experimental do conhecimento matemático, podendo ser representado
pelo seguinte esquema:
Mundo
Físico
Modelagem
matemática
do mundo
Transformação
e operações
matemáticas
Aplicações
ao Mundo
Físico
O que acabamos de explicitar, são algumas formas de identificar o
intuicionismo, na prática pedagógica do professor de matemática. Não pretendemos,
aqui, apresentar conceituações definitivas sobre a concepção intuicionista para o
ensino da Matemática, porém, refletir algumas considerações sobre o conceito de
intuição e seu uso na educação Matemática.
3 AULAS DE MATEMÁTICA: QUE FILOSOFIA ?
Antes de começarmos as explanações referentes às observações das
aulas de Matemática, achamos conveniente que fizéssemos alguns comentários
com relação à escola em que se realizou a pesquisa.
Assim sendo, estaremos destacando as principais características da
escola, (localização, fundação, concepções de ensino aprendizagem explicita no
PPP, etc...), para que posteriormente, frente à análise de dados possamos traçar
alguns encontros e desencontros com relação à proposta de ensino (teoria) e a ação
pedagógica (prática docente), um dos aspectos do nosso objeto de estudo.
3.1 Caracterização da escola
A Escola de Educação Básica João Dagostim é uma escola pública
estadual, localizada no bairro Quarta Linha no município de Criciúma. Atualmente, a
escola conta com 769 alunos, distribuídos nos seguintes cursos: Ensino
Fundamental (1ª a 8ª série) e Ensino Médio (1º, 2º e 3º ano). O Ensino Fundamental
funciona nos turnos matutino e vespertino, com matricula atual de 558 alunos e o
Ensino Médio, no período noturno, com um total de 211 alunos. A matricula da
escola prioriza aqueles que residem ou trabalham na área geográfica onde o colégio
esta localizado. O quadro efetivo de docentes é composto por vinte e cinco
professores. Todos com formação de nível superior, e destes, dezenove possuem
curso de especialização (pós-graduação). Os demais professores, (treze) são
admitidos em caráter temporário. Além destes, a escola possui uma diretora geral e
uma diretora adjunta, uma secretária e seis merendeiras / serventes.
A Escola de Educação Básica João Dagostim, tem uma história de 99
anos. Começou modestamente com uma sala de aula e somente no ano de 1977 foi
transformada em Escola Básica com o nome que mantém, até os dias de hoje,
homenageando uma pessoa da comunidade.
O Projeto Político Pedagógico da escola vem sendo elaborado ao longo
dos últimos dez anos. Antes disso, já havia um regimento escolar e da mesma forma
um planejamento de conteúdos. A partir de 1996, com um evento chamado de DIA
D , a escola iniciou uma série de discussões envolvendo suas necessidades. Foram
abordadas questões relacionadas com aspectos físicos e pedagógicos, sendo que o
segundo item foi mais enfatizado. Fizeram parte do projeto algumas etapas
fundamentais, tais como: discussão das necessidades, elaboração propriamente
dita, execução e avaliação.
O referencial teórico seguido pela escola, baseia-se na Filosofia do
materialismo dialético e na teoria científica do materialismo histórico, cujas
concepções de homem, (partindo do pressuposto de que tudo o que diz respeito à
condição humana tem origem nas relações sociais), sociedade (síntese das relações
sociais de produção
produto e produtor dela) e educação (processo de
humanização do homem em uma sociedade), entendem que os seres humanos
fazem a sua história num mesmo tempo em que são determinados por ela . (MARX,
1978, apud PPP)
No que se refere à concepção pedagógica, a escola pretende seguir a
abordagem Histórico-Cultural, (o termo pretende está entre aspas, porque os
próprios professores admitem que a prática pedagógica está distante do que foi
idealizado). Ainda com relação à prática pedagógica, os professores e os gestores
se reúnem no inicio do ano letivo para delinear os objetivos a serem alcançados. A
partir daí, são realizados encontros com certa freqüência para discussão das
atividades desenvolvidas em sala de aula e na escola, e encontros trimestrais para
elaboração das atividades de aprendizagem que compõem o projeto interdisciplinar
desenvolvido a cada trimestre.
A diretora da escola salienta a cada encontro que são poucos os
professores que se dedicam ou se interessam no aprofundamento teórico, de forma
espontânea. Os espaços pedagógicos se articulam da mesma forma, na
espontaneidade,
em relação aos conceitos que estão sendo desenvolvidos. A
escola vê o saber científico como decorrência de uma boa proposta pedagógica e de
fatores externos (sociais). Consta no Projeto Político Pedagógico que apropriação de
novos conceitos se faz necessária para a evolução da humanidade.
A diretora da escola, nas reuniões pedagógicas, deixa claro que a
produção do conhecimento, nesta escola, se efetiva parcialmente, pois muitos são
os profissionais que confundem mera informação com apropriação de conceitos. Os
alunos são avaliados através de testes, trabalhos e demais atividades desenvolvidas
no decorrer dos bimestres.
Ainda com relação à produção de conhecimento, a diretora, Iracema
Rosso de Souza, em uma das reuniões pedagógicas desabafa: ...a produção de
conhecimento se reverte no maior problema de uma escola, quando se vive em
conflito e não conseguimos encontrar mecanismos suficientes que nos permitam
alcançar nossos objetivos, quando estes mesmos objetivos não coincidem com os
manifestados pelos alunos, quando não conseguimos pensar uma forma de utilizar o
que o aluno traz e sim somente o que achamos que se faz necessário: é como se o
aluno nunca soubesse nada... .
Tal manifestação expressa que há algo estagnado na prática docente dos
professores da escola que precisa ser rompido. A estagnação tem seus valores e
concepções que precisam ser estudados e entendidos para que se possa fazer algo.
3.2 Primeira Aproximação
Após terminarmos o pré-projeto de pesquisa, (que serviu como requisito
parcial para aprovação na disciplina do professor Ricardo Luiz de Bitencourt
Metodologia e Método da Pesquisa em Educação) e do contato com o orientador
(professor Dr. Ademir Damazio), algumas questões, como, por exemplo, contato
com a escola, conversa com as professoras que fariam parte da pesquisa, turmas
que seriam observadas, etc..., começaram a exigir providências.
Sendo assim, no mês de julho de 2004, por meio de conversas informais,
solicitamos autorização para as colegas de escola, (J, professora de 5ª a 8ª série do
ensino Fundamental e A, professora do 1º, 2º e 3º ano do Ensino Médio), para que
observássemos algumas de suas aulas, com a finalidade de responder a questões
pertinentes às atividades da pós-graduação (especialização). É necessário enfatizar
que, inicialmente, não contamos que seria a pesquisa da monografia, pois
preferimos evitar acanhamentos. Salientamos, da mesma forma, que não utilizamos
questionários como instrumento para coleta de dados, em primeiro momento, porque
não estávamos medindo o conhecimento das colegas referente à filosofia da
educação matemática. Por outro lado, não gostaríamos que as profissionais
manifestassem qualquer constrangimento por acreditarem que estavam sendo
avaliadas ou analisadas. Não combinamos nada, conforme a oportunidade
estaríamos presentes nas aulas. Na mesma semana, a professora J precisou se
ausentar da escola e aproveitamos a ocasião para substituí-la. Estava estabelecido
o primeiro contato com os alunos. Eram duas turmas, uma sétima e uma quinta
série. Inicialmente, não foram feitas anotações, pois queríamos verificar quais os
conteúdos estudados, as manifestações dos alunos, as dificuldades apresentadas e
como se comportavam frente às dúvidas
apresentadas
nas
aulas.
Naquele
mesmo dia, a professora A tinha cinco aulas no período noturno. Aproveitamos a
ocasião e nos fizemos presentes em algumas delas. Após o final das aulas,
confesso que me sentia perdida, sem saber que rumo tomar. Na sétima série, o
conteúdo estudado era grau de polinômios, os alunos demonstravam tamanha
confusão. Na quinta série, resolução de problemas, ninguém se entendia. No ensino
médio 1º ano, função polinomial do segundo grau (quadrática), os alunos estavam
mais calmos, algumas dúvidas foram manifestadas, a professora fez algumas
intervenções e logo em seguida a aula terminava.
Após algumas reflexões, concluímos que nos faltavam leituras que
pudessem servir de embasamento para nossas observações. Decidimos então, dar
início à fundamentação teórica e, desta forma, determinamos que começaríamos a
fazer novas observações em agosto, no retorno das férias.
3.3 Acompanhamento das aulas
Observações, investigações, dúvidas
Que
Filosofia é esta?
Quando retornamos das férias, iniciamos as observações.
Porém,
preferimos escolher somente uma turma do ensino fundamental (sétima série) e
outra do ensino médio (1º ano).
Começamos nossas observações com a sétima série. A professora J, foi
para sala de aula e, em seguida, fomos ao seu encontro.
No quadro verde estavam as seguintes figuras:
1
A = X . X = X2
X
X
A=X.1=X
1
A = 1.1= 1
X
1
Observamos
que a professora J, estava
estabelecendo uma relação entre
as áreas encontradas nas figuras geométricas com a representação de adição de
polinômios.
A lei era a seguinte: figuras azuis
sinal positivo
figuras vermelhas
sinais negativos
A alerta era de que: não se poderia somar figuras diferentes, pois estas
não representam a mesma área; figuras com cores diferentes, se anulam.
Terminada a explicação, a professora propôs uma série de atividades para
que os alunos resolvessem em aula. A atividade era a seguinte:
1) Represente geometricamente os seguintes polinômios:
(citamos somente a questão a, pois as demais são similares)
a) 2x2 + 3x + 5
A resposta de grande parte dos alunos foi esta:
1
X²
X²
X
X
X
1
1
1
1
Não precisou de muito tempo para que os alunos completassem as
atividades com êxito.
Então a professora J colocou a seguinte questão no quadro verde:
2) Qual o polinômio resultante da adição representada abaixo:
+
O número de acertos havia diminuído, com relação à atividade anterior.
Observamos que algumas dúvidas começaram a surgir, porém se referiam as
operações com números relativos.
Com relação a este fato, Kline (1976), comenta que ao formar matemática
construtivamente, o principio genético se manifesta útil como um guia. Este princípio
diz que a ordem histórica é geralmente a ordem certa e que as dificuldades
experimentadas pelos próprios matemáticos são justamente as dificuldades que os
estudantes experimentarão. Nisso inclui-se principalmente os números irracionais,
negativos e complexos.
A aula chega ao final. Saímos conversando sobre o assunto. A professora
J nos confessava que ainda se sentia um pouco insegura ao trabalhar polinômios
representando-os geometricamente. Percebemos nela certo constrangimento.
Sendo
assim,
perguntamos
se
incomodávamos
ou
atrapalhávamos
o
desenvolvimento das aulas ao que ela respondeu negativamente.
De acordo com os fatos ocorridos já na primeira aula com J, verificamos a
importância de salientar que a referida professora estava fora da sala de aula por
mais de dezesseis anos. Nesse período, ocupava o cargo de diretora da escola.
Outra questão que não podemos perder de vista é que as aulas das duas turmas de
sétima série do período vespertina eram ministradas pela professora em questão, e
nas sétimas séries do período matutino, somos nós os mediadores do processo de
ensino aprendizagem.
Na aula seguinte, a minoria dos alunos demonstrou interesse em
responder a questão proposta na aula anterior. A professora começou a desenhar as
figuras geométricas no quadro verde com o objetivo de dar início às explicações.
Neste momento, um aluno pede para fazer a atividade no quadro e a
professora permite. O procedimento adotado pelo aluno foi o seguinte:
+
Resposta: 7x2
3x
2
A professora perguntou:
Profª : Como obteve a resposta?
Aluno: Cancelei todo positivo com o negativo.
Profª: O que significa cancelar?
Aluno (já parecendo arrependido de estar ali): cancelar..., acho que é
anular...
Profª: E com as figuras da mesma cor, o que você fez ?
Aluno: Somei porque tinham a mesma cor...
A professora pediu ao aluno que sentasse, perguntou aos demais alunos
da turma se apresentavam alguma dúvida. Como não responderam nada, começou
a passar mais atividades no quadro.
A atividade era a seguinte:
3) Utilizando as figuras, faça a adição de polinômios abaixo, transformando-os
para a forma algébrica e em seguida encontrando o seu valor numérico,
conforme o valor de x em cada questão.
a)
+
Para x = 2
Colocamos como exemplo somente um item da atividade proposta, pois as
demais apresentavam as mesmas características desta.
Chamou-nos a atenção o fato de que ao trabalharem do geométrico para o
algébrico (intuição para formalização) os alunos não manifestavam dúvidas. Porém,
no momento em que tinham que calcular o valor numérico da expressão, quando
x=2 (algébrico para o aritmético), não conseguiram chegar na resposta.
Lembramos, nesta ocasião da fala de Costa (1971, p.156), quando
menciona:
...a intuição é uma faculdade da mente que conhece imediatamente; isto é,
a intuição não depende de qualquer meio para fazer o conhecimento. Em
particular, a intuição é independente da razão e da linguagem, (estes
elementos passam a ser somente uma ajuda à memória). O resultado da
atividade construtiva da mente, porém é conhecido absolutamente certo e
evidente (porque construído).
Sendo assim, não é difícil de perceber que os alunos utilizaram a intuição
na busca de respostas aos exercícios propostos. Mas, ao se depararem com uma
atividade formalizada que exigia conhecimentos matemáticos, não conseguiram
discernir o resultado esperado.
O intuicionismo na filosofia da matemática significa uma abordagem à
matemática de acordo com a atividade mental imediata e construtiva dos humanos.
Desta forma, não objetiva conduzir os alunos às múltiplas significações dos
conceitos. Verificamos, então, que atividade mental imediata, ou seja, a intuição
poda o desenvolvimento do pensamento matemático, visto que este se fundamenta
em reflexões e pensamentos profundos que não se limitam aos imediatos.
O que mencionamos, anteriormente, não quer dizer que as atividades
desenvolvidas com figuras geométricas são indicadas como errôneas, porque
conduzem os alunos ao pensamento intuitivo, mas sim porque não se verifica a
apropriação de conceitos em sua totalidade.
Na aula seguinte, a professora J propôs o inverso, ou seja, a atividade
consistia em passar do algébrico para o geométrico. Os alunos não manifestaram
dificuldades. Nas aulas que se seguiram, verificamos que os estudantes
apresentavam mais segurança em adicionar e subtrair polinômios sem a ajuda das
figuras geométricas. Podemos, então, inferir que tais estudantes chegaram a
concretizar o processo de formalização. Ou seja, fazer uso de símbolos e regras
aleatoriamente, sem compreender as significações matemáticas envolvidas no
processo.
Porém, quando a professora J começou a ensinar multiplicação de
polinômios, a história começou a mudar de rumo.
A professora J começou a aula com as seguintes figuras geométricas,
dispostas no quadro:
Como:
x2 =
x=
1=
A atividade consistia no seguinte:
Ao prolongarmos as extremidades de cada figura, fazendo com que as
mesmas se encontrem obteremos a resposta da multiplicação dos polinômios,
através das figuras formadas no cruzamentos de ambas projeções. Logo, a resposta
da multiplicação de 2x. (2x + 3) = 4x2 + 6x
O resultado foi, momentaneamente muito bom, pois todos os alunos
conseguiam multiplicar polinômios geometricamente. Com o desenrolar das aulas,
sem o auxilio geométrico, pouquíssimos chegaram a respostas satisfatórias. Neste
sentido, percebemos que o processo de formalização não se concretizou, muito
menos a apropriação de significação de conceitos.
Para Kline (1976), ensinar intuitivamente não é tarefa indicada, porém, no
hábil emprego do processo de descoberta, despertamos no aluno o prazer da
realização. Além disso, colaboramos para que os mesmos encontrem um resultado
independente dos meios. Contudo, esta descoberta não bastará por muito tempo. A
prova dedutiva é o que viabiliza a aceitação de um resultado para o corpo da
matemática. Sendo assim, se a mesma não se concretizar, (formalização), voltamos
à estaca zero.
Continuamos nossas observações, agora no 1º ano do Ensino Médio, com
a professora A. Não podemos deixar de apontar que em todos os momentos que
conversávamos com a professora J, a professora A, estava presente. Isto se deve
principalmente por termos atividades de aprendizagens em comum, (éramos
professoras do 1º ano do ensino médio no turno matutino
turma especial).
Quando entramos na sala de aula a professora já havia começado a
passar atividades. O conteúdo era função polinomial do 2º grau.
Uma atividade que nos chamou a atenção foi a seguinte:
3) Encontre os zeros de cada uma das funções, em seguida, classifiqueas em polinomial do 1º grau ou quadráticas. Logo após, construa seus respectivos
gráficos:
Na questão d , ocorreu o seguinte fato:
d) f(x) = x2
x2
4
4=0
x2 = 4
x=
O aluno pergunta:
4
x=±2
Aluno: Professora porque a resposta é ± 2 ?
A professora responde gentilmente:
Profª: Por que (-2)2 = 4 e da mesma forma 22 = 4.
A esta observação, chamamos de formalismo vulgar, por se tratar de uma
formalização simplória, ou seja, que não exige e não faz uso do rigor das provas
axiomáticas.
O procedimento formalista correto a ser adotado para explicação ao aluno
seria:
f(x) = x2
x2
4
4=0
( x + 2 ) . (x
x = -2
2) = 0
x = +2
Ainda em cada passo ou afirmação seria ideal justificar indicando a
propriedade ou a definição utilizada.
Da mesma forma, surpreendemo-nos ao verificar que os alunos,
objetivando encontrar os zeros da equação de primeiro grau, procederam da
seguinte forma:
c) f(x) = 3x - 12
3
12 ² 4.( 3 ).0
2 .1
3
x´=
3 12
2.1
144 0
2 .1
9
2
e
x´´=
15
2
Os alunos procuraram os zeros de uma equação do primeiro grau, com os
procedimentos formais utilizados para resolver uma equação do segundo grau. Isto
nos mostra que tais alunos, não compreendem o sentido da palavra Grau de uma
equação.
Uma definição, bastante formal, porém exata, seria a seguinte:
O grau de uma equação é indicado pelo maior expoente da incógnita e
indica o número de raízes que possui. Assim:
* A equação x2
4 = 0, constitui uma equação polinomial do 2º grau, pois
x apresenta grau 2, sendo assim, possuirá duas raízes;
* A equação 3x
9 = 0, constitui uma equação do 1º grau, pois x
apresenta grau 1, sendo assim, possuirá uma raiz real.
Segundo Costa (1962), o método axiomático encontra aplicação prática em
toda a matemática, constituindo-se hoje, na técnica básica desta ciência. O
formalismo, em poucas palavras, deseja transformar o método axiomático, de
técnica que é, na essência mesma da matemática.
Moisés (1997) afirma que, embora no campo da Educação Matemática se
debatam novas propostas para um ensino de Matemática que proporcione realmente
seu aprendizado, no Ensino Fundamental e Médio, uma quantidade enorme de
informações é ainda despejada sobre os estudantes como se os mesmos fossem
seres desprivilegiados de raciocínio e capacidade de pensar. Esse tipo de prática
pedagógica, que é adotada quase que unanimemente nas escolas, tem o efeito
perverso
de
oferecer
e
fortalecer
uma
única
concepção
de
ensino
(positivista/formalista).
Algumas aulas se passaram e nós continuamos observando-as
atentamente, na busca de informações que contribuísse significativamente com
nossa pesquisa. Entre alguns intervalos, mantínhamos conversas que denunciavam
a decepção dos resultados obtidos com relação à aprendizagem dos alunos durante
o ano letivo vigente. Aproveitamos a oportunidade para confessarmos às colegas
que a pesquisa em foco se tratava da monografia de pós-graduação. Tanto a
professora J, quanto a professora A, confessaram o desencanto pela profissão em
seus discursos.
Algumas destas falas demonstraram importância incalculável
para nossa pesquisa. A professora J mencionou o seguinte:
Profª: ...eu tento, mas não sei mais o que fazer. Procuro atividades
diferenciadas, não agüento mais carregar tantos livros. Não sei, acho que
desaprendi de dar aula, ou sei lá, talvez nunca tenha aprendido...
A outra professora completa afirmando:
Eu também tento, tô sempre correndo atrás, me dedico sempre que
posso, ás vezes chego a ficar até as 2:00h da manhã preparando atividades e
tentando encontrar uma maneira de fazer esses alunos aprender. Parece que falta
alguma coisa nas aulas. Tenho a impressão que elas estão sempre incompletas. No
tempo em que nos formamos, não tínhamos as informações que hoje o pessoal
mais novo tem .
Neste momento, uma série de lembranças me ocorreram durante minha
formação discente. Acreditávamos que tínhamos encontrado um dos personagens
principais responsáveis pelo caos da educação desde muitos tempos, até a
atualidade: a formação dos professores.
Isto mesmo, aquela formação marcada pela extrema linearidade
positivista incutida a muito em nossa sociedade e impulsionada pelo método
rigoroso de Descartes, desde o século XVI / XVII.
Cabe-nos, desta forma, as seguintes perguntas:
Como tentar fugir desta linearidade, que se apresenta nas reuniões
pedagógicas da escola, nos projetos interdisciplinares, nas atividades de
aprendizagem e inclusive nos cursos de capacitação de professores?
Como casar teoria, (que também se manifesta com falhas, desde o
Projeto Político Pedagógico até a Proposta Curricular), com a tão sonhada prática
pedagógica
constituída
de
sólida
fundamentação
teórica
alicerçada
em
pressupostos filosóficos coerentes de forma que não vise à educação como
elemento de hierarquia social?
Um(a) professor(a), certamente gostaria de transcender sua prática
pedagógica pela construção de um referencial teórico norteador de suas atividades
escolares. Porém a efetivação do desejo, tropeça na falta de tempo disponível para
percorrer calmamente uma reflexão continuada. A sociedade bloqueia o professor
no caminho a ser percorrido em busca de sua profissionalização como intelectual,
quase que o obrigando a ser um mero repassador de conteúdos e impedindo-o de
participar do exercício da pesquisa.
Percebe-se, então, como a prática pedagógica enfadonha, ao lado de
outros fatores, impede que a maioria dos professores das escolas públicas adquirir
uma visão intensa e plena sobre os aspectos psico-pedagógico-culturais de seu
trabalho. Por sua vez, esta falta de visão não lhes permite elaborar propostas
cientifico-didáticas praticáveis para superar as dificuldades, deficiências e
impropriedades encontradas no ato pedagógico de ensinar.
4
CONCLUSÃO
Nesta
pesquisa,
apresentamos
nossas
entendimentos que duas professoras de Matemática
investigações
acerca
dos
uma do Ensino Fundamental
e outra do Ensino Médio - apresentam com relação ao ensino de Matemática e a
formação de professores, tendo como base algumas concepções de Filosofia da
Educação Matemática.
Nossas observações foram feitas em duas turmas, uma do Ensino
Fundamental (7ª série), com a professora J e outra no Ensino Médio (1º ano), com a
professora A, durante o terceiro bimestre do ano letivo de 2004.
Para que pudéssemos analisar os dados obtidos, nos apoiamos em
Bicudo, Garnica e Miguel (2003), quando afirmam que a Filosofia da Educação
Matemática se refere a uma abordagem filosófica da educação matemática, que nos
permite avaliar intenções, finalidades, propósitos e valores subjacentes à educação
matemática, tematizando criticamente seus objetos, objetivos, métodos, a sua
significação e relevância social.
Em reuniões destinadas ao planejamento de atividades de aprendizagem
procurávamos fazer do questionamento um fato sempre presente. Para nós,
questionamento , significava perguntar-se: Como ensinar?, O que ensinar?, Qual o
significado disso, (a matemática), para o aluno?
Durante as aulas de Matemática, apesar de todos os esforços para promover o
abandono à pedagogia fundamentada numa formalidade, (que preferimos chamar de
formalismo vulgar, pois não apresenta axiomas ou postulados para provar as
verdades matemáticas), verificamos que posturas e valores, próprios da filosofia
positivista insinuam-se, são reproduzidos, fortalecidos e legitimados.
A realidade da sala de aula mostrava-se com estranheza. As atividades
preparadas tomavam formas diferentes ao serem aplicadas na prática da sala de
aula. Na escola, parece ser natural que a forma de argumentação utilizada para
garantir a validade do conhecimento matemático seja, na maioria das vezes, a
demonstração formal.
Percebemos, desta forma, como a prática pedagógica
rotineira ,
impregnada da formalidade vinda da filosofia positivista, impede que os professores
adquiram uma visão global sobre os aspectos pedagógicos e sociais do seu
trabalho. Esta falta de visão, não lhes permite elaborar propostas de atividades
pedagogicamente
favoráveis
para
superar
as
dificuldades,
deficiências
e
impropriedades, encontradas na prática pedagógica.
Ficou evidente, então, que não adiantava prepararmos inúmeras
atividades com vistas a uma metodologia que não comungava com a filosofia e a
concepção de ensino que as professoras apresentavam. Não bastava querer se
inserir numa concepção pedagógica, sem acreditar, apostar, defender e, sobretudo,
lutar por ela. É como uma filosofia de vida, que você defende e mantém porque é
assim que você prefere e gosta de viver.
Verificamos, então, que a impregnação de uma formação linear, não
permitiu que as professoras, mesmo com muito esforço, delineassem um caminho
pedagogicamente articulado, que as permitissem, aos poucos, se libertarem de um
método ou de uma forma de ver a ciência imposta para a sociedade desde o
século XVII, (Discurso do Método
René Descartes).
Não seria nenhuma surpresa, desta forma, anunciar a presença marcante
das correntes em filosofia da matemática nas atividades pedagógicas desenvolvidas
em sala de aula.
Tudo se combinava, a linearidade explicita na formação das professoras, e
a filosofia formalista e intuicionista que se evidenciava a cada atividade. Ambas
frutos do mesmo pomar .
Cabe-nos apontar, que não estamos criticando ninguém, na verdade
estamos analisando os fatos, apontando concepções de ensino, traçando um perfil
da formação na qual também somos vítimas. Afinal, o sistema e a metodologia no
domínio da educação têm se caracterizado por um processo consistindo em fornecer
respostas a questões que jamais foram postas pelos participantes. Um processo
imitativo e acrítico no qual as respostas não são produzidas a partir da reflexão de
um indivíduo, ou grupo deles, sobre sua ação em uma dada realidade. Assim sendo,
esse processo e suas respostas ignoram a característica diversa e multiforme da
realidade e incorrem, geralmente, no erro de identificar método e modelo.
Os professores de matemática apontam as suas dificuldades no
enfrentamento das questões que não satisfazem seus ideais a respeito da relação
com seus alunos e a conseqüente aprendizagem. Eles têm consciência de que há
algo errado e até buscam alternativa de apresentação de conteúdos para seus
alunos como, por exemplo, ensinar operações de polinômios com figuras
retangulares. No entanto, revelam uma certa ingenuidade em acreditar que aquele
ato daria resposta imediata as suas angústias. Não há um entendimento de que
subjacente àquela apresentação de conteúdo, aos alunos, existe uma concepção de
matemática, de ensino e de aprendizagem que penetra com a maior facilidade nas
concepções já arraigadas. Portanto, não oportuniza a problematização do real
pedagógico estabelecido a luz de algo
teoria - já assumido com conhecimento de
causa. Fica evidente que é a característica externa da ação de expor um conteúdo
que proporciona aprendizagem do aluno e a conseqüente superação dos problemas
a que ela veio. Questões internas da matemática e do processo pedagógico são
despercebidos pelos professores. Para estes, a
matemática
é um
todo
inquestionável.
De modo algum admitem que os fundamentos da matemática estão
constantemente sendo colocados em xeque a ponto de emergirem explicações
filosóficas para apagar o incêndio. Assim formalismo, logicismo e intuicionismo não
fazem parte do vocabulário e, conseqüentemente, do referencial teórico dos
professores.
Nesse contexto produzido, historicamente, gerou-se professores com
convicções acirradas e, contraditoriamente, geradora de ingenuidade teórica que os
levam a viver pedagogicamente sempre em estado de angústia e de impotência. É
impossível, pois, não fazer o questionamento: Então, os professores de matemática
vivem num obscurantismo que impede de entender as múltiplas determinações da
sua docência? A resposta a ser construída, na certa, exigirá estudo futuro mais
aprofundado.
Porém, nada impede de apontarmos as possibilidades de uma pedagogia
que contribua para crítica efetiva dos sujeitos sobre o processo de significar e
ressignificar conceitos. Tal pedagogia deveria fundamentar-se numa concepção que
recupere o sentido social, humano e solidário do ato de conhecer. Precisamos sair
da menoridade, como sabiamente afirmava Kant. Para isso, precisamos acreditar
que - antes do educador instituir objetivo ou atividade teórica ou prática em que a
finalidade seja o ensino da matemática - o educador precisa saber responder as
questões filosóficas sobre a natureza e a finalidade da ciência que fundamenta a
disciplina que leciona e da educação. Só assim, estará alerta paro fato de que o
modo como é manifestado o fazer educativo, pode estar colaborando para a
formação de um indivíduo com ideais transformadores ou pode ser também a
reprodução da alienação. (DUARTE, 1993)
Diante desse contexto de consciência frágil a respeito das questões sobre
a matemática e de seu ensino, adotamos como tema do nosso projeto de mestrado
as concepções de educação e de filosofia da educação matemática inseridas no
contexto da formação de professores durante sua formação universitária.
Isso
significa dizer que desponta uma nova etapa da presente pesquisa que se edificará
nas reflexões sobre a prática pedagógica no ensino superior, com um olhar da
filosofia da educação matemática.
REFERÊNCIAS
ABBAGNANO, Nicola. Dicionário de filosofia. 4 ed. São Paulo: Martins Fontes,
2000.
ALENCAR FILHO, Edgard de. Iniciação à lógica matemática. 10 ed. São Paulo:
Nobel, 1978.
ARANHA, Maria Lúcia de Arruda; MARTINS, Maria Helena Pires. Filosofando:
introdução à filosofia. 2. ed. rev. e atual. São Paulo: Moderna, 1986.
BARKER, Stephen F. Filosofia da Matemática. Rio de Janeiro: Zahar, 1970.
BASSANEZI, Rodney. Modelagem matemática.Dynamis, Blumenau,v.1, n. 7,
abr/jun. 1994.
BICUDO, Maria Aparecida Viggiani. Filosofia da educação matemática
concepções e movimento. Brasília: Plano, 2003.
________. Pesquisa em educação matemática: concepções e perspectivas. São
Paulo: UNESP, 1999.
BICUDO, Maria Aparecida Viggiani; GARNICA, Antonio Vicente Marafioti. Filosofia
da educação matemática. Belo Horizonte: Autêntica, 2003.
BORNHEIM, Gerd A. Introdução ao filosofar. 7 ed. Porto Alegre: Globo, 1969.
CARAÇA, B.de Jesus.Conceitos fundamentais da matemática. Lisboa: Gradiva,
1998.
CARVALHO, Roberto Lins de; OLIVEIRA, Cláudia Maria G.M. de. Modelos de
computação e sistemas formais. Rio de Janeiro: DCC/IM, COPPE/Sistemas,
NCE/UFRJ, 11a Escola de Computação, 1998.
CHAUÍ, Marilena de Sousa. Convite à filosofia. 11 ed. São Paulo: Ática, 1999.
CORBISIER, Roland. Enciclopédia filosófica. 2 ed. Rio de Janeiro: Civilização
Brasileira, 1987.
COSTA, Manoel Amoroso. As idéias fundamentais da matemática e outros
ensaios. São Paulo: Grijalbo, 1971.
COSTA, Newton Carneiro A. Introdução aos fundamentos da matemática. Porto
Alegre: Globo, 1962.
COTRIM, Gilberto. Fundamentos da filosofia: ser, saber e fazer. 8 ed. São Paulo:
Saraiva, 1993.
CYRINO, Hélio; PENHA, Carlos. Filosofia hoje. 3 ed. Campinas: Papirus, 1986.
DAVIS, Phiplip J; HERSH, Reuben. A experiência matemática. Rio de Janeiro:
Francisco Alves, 1986.
DUARTE, Newton. A relação entre o lógico e o histórico no ensino da
matemática elementar. 1987. 185 f. Dissertação. (Mestrado em Educação e
Ciências Humanas) Programa de Pós-Graduação em Educação PPGE
Universidade Federal de São Carlos São Carlos.
________. A individualidade para-sí. Campinas: Autores Associados , 1993.
E.E.B.JOÃO DAGOSTIM. Projeto político pedagógico. Criciúma, 2004.
FALVETTA, Ricardo. A Matemática pulsa no dia-a-dia. Revista Nova Escola, São
Paulo: Abril, dez./ 2004, p. 18-22.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino de matemática no
Brasil. Revista Zetetiké, Campinas, ano 3, n 4, 1995.
FROTTA, Paulo Rômulo de O. Em busca de um novo paradigma para a formação de
licenciados em ciências. In FROTTA, Paulo R. de O. (org). Do cotidiano a
formação de professores. Teresina: UFPI, 2003.
GADOTTI, Moacir. Concepção dialética de educação: um estudo introdutório.
9 ed. São Paulo: Cortez, 1995.
_________. Educação e poder introdução a pedagogia do conflito. São Paulo:
Cortez, 1980.
JOLIVET, Regis. Curso de filosofía. 18 ed. Rio de Janeiro: Agir, 1990.
KLINE, Morris. O fracasso da matemática moderna. São Paulo: Ibrasa, 1976.
KÖRNER, S. Uma Introdução à Filosofia da Matemática. Rio de Janeiro:
Zahar,1985.
LIBÂNEO, José Carlos. Didática. São Paulo: Cortez, 1994.
MACHADO, Nilson José. Matemática e língua materna: análise de uma
impregnação mútua. 4.ed. São Paulo: Cortez, 1993.
_________. Matemática e realidade. São Paulo: Cortez, 1985.
MANACORDA, Mário Alighiero. Marx e a pedagogia moderna. 2 ed. São Paulo:
Cortez, 1996.
MANNO, Ambrosio Giacomo. A Filosofia da matemática. Lisboa: Edições 70, sd.
MOISÉS, Lúcia. Aplicações de Vygotsky á Educação Matemática. Campinas:
Papirus, 1997.
NUNES, César Aparecido. Aprendendo Filosofia. Campinas: Papirus, 1996.
PAVANELLO, Regina Maria. A pesquisa na formação de professores de matemática
para a escola básica. Educação Matemática em Revista. São Paulo: SBEM, p. 8
13. dez. 2003.
REVUZ, André. Matemática Moderna, matemática viva. Portugal : Livros
Horizontes, sd.
RUSSEL, Bertrand. Introdução à filosofia da matemática. 3 ed. Rio de Janeiro:
Zahar, 1974.
SANTA CATARINA. PROPOSTA CURRICULAR. Educação infantil, ensino
fundamental e ensino médio. Disciplinas Curriculares. Florianópolis:
SED/COGEN/DIEF, 1998.
SAVIANI, Dermeval. Educação: do senso comum à consciência filosófica. São
Paulo: Cortez e Autores Associados, 1980.
_________. Escola e democracia: polêmicas do nosso tempo. São Paulo: Autores
Associados, 2000.
SCHEIBE, Leda; DARÓS, Maria das Dores. Formação de professores em Santa
Catarina. Florianópolis: Centro de Ciências da Educação da UFSC Núcleo de
Publicação NUP, 2002.
SOARES, Eliana Maria do Sacramento. Formalização e intuição no contexto do
conhecimento do conhecimento, do ensino e da atuação social. Revista Zetetiké,
Campinas: ano 3, n. 3, 1995.
TELES, Antônio Xavier. Introdução ao estudo de filosofia. 13 ed. São Paulo: Ática,
1975.
VASCONCELLOS, Claudia Cristina C. A filosofia da matemática. Disponível em 15
jan. 2001, (http://www.ipv.pt/millenium/millenium_9.htm)
VIANNA, Carlos Roberto. Matemática e História: Algumas relações e implicações
pedagógicas. 1995. 178 f. Dissertação. (Mestrado em Educação) Programa de
Pós-Graduação em Educação. Universidade de São Paulo, São Paulo.
ZIMBARG, Jacob. Introdução à lógica matemática. São Paulo: Instituto de
Matemática Pura e Aplicada, 1973.
This document was created with Win2PDF available at http://www.win2pdf.com.
The unregistered version of Win2PDF is for evaluation or non-commercial use only.