Fundamentos da Didáctica da Matemática
2006/2007
Professor Doutor João Pedro da Ponte
A Experiência Matemática
Davis, P.J., & Hersh, R.
Trabalho realizado por:
Cláudia Gardete nº 26009
Evangelina Romano nº 34251
Sandra Cadima nº 34242
A Natureza da Matemática
Dogmas
Platonismo:
Os objectos matemáticos
são reais.
A existência desses
Formalismo:
Não há qualquer
objecto matemático.
A Matemática é um
objectos é um facto objectivo
conjunto de axiomas,
e independente do nosso
definições e teoremas.
conhecimento.
São imutáveis – não
foram criados, não se
alterarão ou desaparecerão.
Sucessão de
fórmulas.
Construtivismo
Matemática
genuína é só a que
pode ser obtida por
construção finita.
Mito de Euclides
Crença de que os livros de Euclides contêm verdades sobre o Universo
que são claras e indubitáveis
Até fins do século XIX
Não tinha discussão
Era inatacável
Todos acreditavam nele
“Até hoje parece que todas as pessoas cultas acreditam no mito de
Euclides.”
(Davis & Hersh, 1995, p. 305)
Matemática per si
Geometria (até séc. XIX)
Descoberta de geometrias
Desenvolvimento da análise
não euclidianas
Perda da certeza na geometria
Perda de qualquer certeza no
conhecimento humano
Mudança dos
fundamentos para a
aritmética
Teoria dos conjuntos
Russel (Paradoxos)
Lógica intuitiva mais arriscada que a
Matemática Clássica
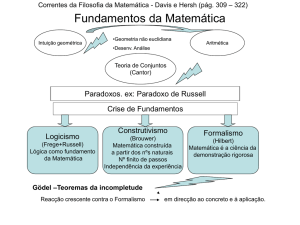
A crise dos Fundamentos
Fim do século XIX
Discrepância
Ideal tradicional da Matemática
Mito de Euclides
A realidade da Matemática
Prática real da actividade matemática
num determinado período
Platonismo
Geometria
Escolasticismo
Racionalismo
Razão como característica inata da
mente humana.
A Matemática e a Religião são os
melhores exemplos do conhecimento.
Ajudou à evolução da Ciência.
Materialismo
Empirismo
Todo o conhecimento
provém da observação
excepto o matemático.
Surgem 3 escolas:
Logicismo
Fracassou
1884 – Frege
1910 – Russell & Whitehead
“Principia Mathematica”
Construtivismo
Desprezado
1908 – Brouwer
Intuicionismo
Formalismo
Derrotado por Gödel
1910 - Hilbert
A Matemática consiste
apenas em axiomas,
definições e teoremas
Logicismo
Construtivismo
Formalismo
Guerrearam entre si durante trinta ou quarenta anos.
Nenhuma podia fazer muito pelos fundamentos.
Não existem conclusões quando terminam.
Logicismo
A Matemática Clássica era parte da Lógica.
Iniciou-se com Frege e Russell.
Reformulação da teoria de conjuntos que evitasse o paradoxo
de Russell e assim salvar o seu projecto de estabelecer a
Matemática tendo a Lógica como fundamento.
Estrutura demasiado complexa.
Afasta-se da Lógica ao excluir os paradoxos da
teoria de conjuntos.
Construtivismo
L. C. J. Brower – 1908
Intuicionismo - forma mais conhecida do Construtivismo.
É a intuição que determina a coerência e a aceitabilidade das
ideias e não a experiência, nem a lógica.
Os números naturais são-nos dados a conhecer por uma intuição
fundamental que é o ponto de partida para toda a Matemática.
Formalismo
Iniciou-se com Hilbert (1910).
Objectivos de Hilbert:
Encontrar uma técnica matemática por meio da qual se demonstrasse
que a Matemática estava livre de contradições.
Defender a Matemática da crítica de Brouwer.
O formalismo contemporâneo descende do formalismo de Hilbert
Acreditava na realidade matemática finita
Inventou a metamatemática
Matemática como a ciência da demonstração rigorosa.
Domínio do formalismo deveu-se à sua ligação com o positivismo lógico.
A Matemática é vista não como uma ciência mas como uma linguagem
para as outras ciências.
Recentemente tem crescido uma reacção contra o formalismo.
A investigação direcciona-se para o concreto e para a aplicação.
Menos rigidez na exposição formal.
A Filosofia formalista está em vias de perder o seu estatuto privilegiado.
Lakatos e a teoria da falibilidade
Mostra a desadequação do formalismo e
cria a imagem de uma matemática viva e
em desenvolvimento.
Não cumpre o
programa de
reconstruir a
filosofia da
O Logicismo e o
Proofs and refutations
matemática
É possível uma Filosofia
como uma
Popperiana da Matemática.
epistemologia da
falibilidade.
Formalismo são inaceitáveis.
Esquema não adequado
para explicar o
desenvolvimento de todos
os ramos da matemática.
Matemática Real
Versus
Demonstrações:
Estabelecidas através
do consenso de pessoas
Metamatemática
Lógica de primeira ordem
Como actividade faz
parte da Matemática.
“qualificadas”.
Verificáveis dentro
do contexto.
O seu conteúdo retrata
uma estrutura de
demonstrações que é
Se é aceite os resultados são
considerados verdadeiros.
Gerações até serem detectados
erros.
realmente infalível «em
principio».
“Quais são os dados, as «afirmações básicas», do assunto em estudo
que constituem falsificadores potenciais das teorias propostas pela
Matemática Informal?”
(in Davis & Hersh, 1995, p. 326)
É a questão fundamental que tem que ser respondida se
queremos ir mais além na construção de uma epistemologia da
falibilidade ou não dogmática da Matemática.
Lakatos não arriscou e escreveu:
«A resposta, muito provavelmente não será monolítica. Estudos históricocríticos cuidadosos conduzirão a uma solução sofisticada e complexa.»
(in Davis & Hersh, 1995, p. 328)
A Matemática é uma coisa só
Platonistas
Formalistas
Construtivistas
Perspectivas diferentes de um todo.
Cada uma das quais é errada por si só.
Compatíveis no seu todo, quando encaradas sem
preconceito.
Mais recentemente e na linha de Lakatos, proposto por matemáticos, filósofos e
historiadores, surge o quasi-empiricismo.
Questões para debate:
Qual a importância da Filosofia da Matemática nas nossas práticas ?
Qual a influência da evolução dos Fundamentos da Matemática ao nível
do currículo actual?
Existem muitos modos diferentes de olharmos para a Matemática. No
início do século XXI como a encaramos? Qual a que melhor se ajusta à
nossa ideia de Matemática?
Quais os prós e contras da evolução dos Fundamentos para as
práticas? Ter-se-á perdido algo com as incessantes mudanças?