Noções de lógica matemática Conceitos Básicos Noções de lógica

Noções de lógica matemática
Conceitos Básicos
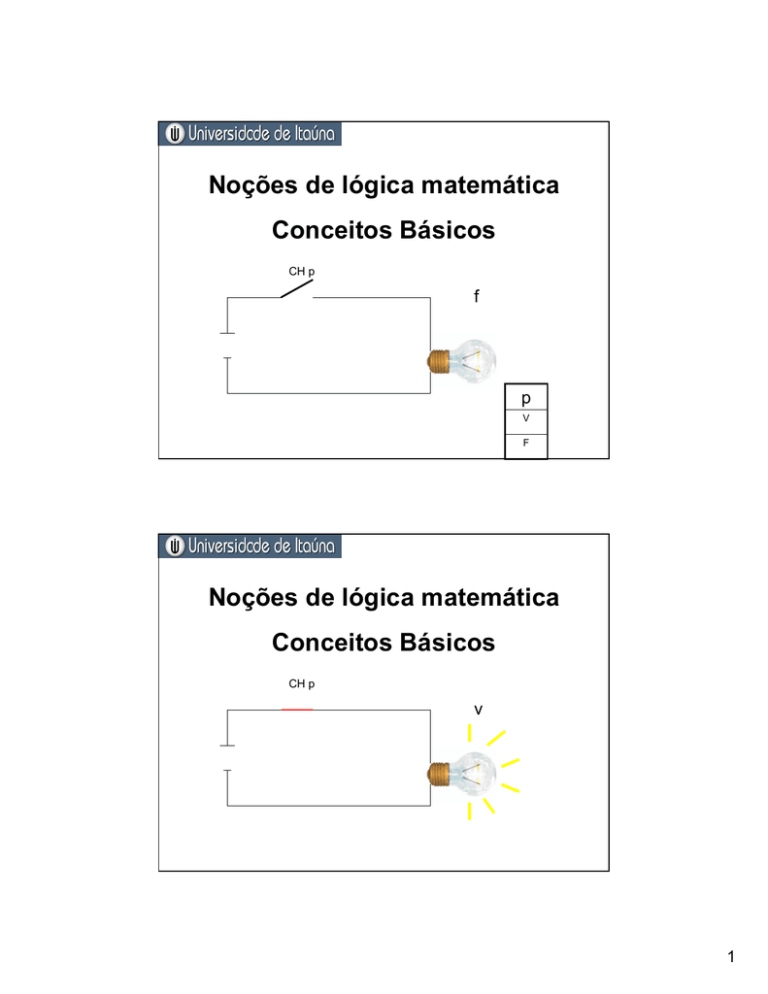
CH p
f
p
V
F
Noções de lógica matemática
Conceitos Básicos
CH p
v
1
Noções de lógica matemática
Conceitos Básicos - E
CH p
CH q
f
p
q
p^q
V
V
V
V
F
F
F
V
F
F
F
F
Noções de lógica matemática
Conceitos Básicos - E
CH p
CH q
v
p
q
p^q
V
V
V
V
F
F
F
V
F
F
F
F
2
Noções de lógica matemática
Conceitos Básicos - OU
CH q
CH p
f
p
q
pvq
V
V
V
V
F
V
F
V
V
F
F
F
Noções de lógica matemática
Conceitos Básicos - OU
CH q
CH p
v
p
q
pvq
V
V
V
V
F
V
F
V
V
F
F
F
3
Noções de lógica matemática
Conceitos Básicos - OU
CH q
CH p
v
p
q
pvq
V
V
V
V
F
V
F
V
V
F
F
F
Noções de lógica matemática
Conceitos Básicos - OU
CH q
CH p
v
p
q
pvq
V
V
V
V
F
V
F
V
V
F
F
F
4
Noções de lógica matemática
Conceitos Básicos
Proposições
Definição: Conjunto de palavras ou símbolos que exprimem um
pensamento de sentido completo. São expressões a respeito das quais tem
sentido dizer que são verdadeiras ou falsas.
Proposição
Valor lógico
O sol é menor do que a Terra
F
Belo Horizonte é a capital de Minas Gerais
V
0.5 é um número inteiro
F
cos(45)=sen(45)
V
A lua é o satélite da Terra
V
Princípios Adotados como Regras Fundamentais do
Pensamento, na Lógica Matemática
Princípio da não contradição - uma proposição não pode ser verdadeira e
falsa ao mesmo tempo.
Princípio do terceiro excluído - toda proposição ou é verdadeira ou é falsa,
isto é, verifica-se sempre um destes casos e nunca um terceiro.
Valores Lógicos das Proposições - chama-se valor lógico de uma proposição
a verdade se a proposição é verdadeira e a falsidade se a proposição é falsa.
Valor Lógico
Símbolo de Designação
Verdade
V
Falsidade
F
Toda proposição tem um e um só dos valores V , F (de acordo os dois princípios citados).
Exemplo:
a) o mercúrio é mais pesado que a água; valor lógico da proposição : verdade (V)
b) o sol gira em torno da Terra; valor lógico da proposição : falsidade (F)
5
Tipos de Proposição
Simples ou Atômicos - é a proposição que não contém nenhuma outra
proposição como parte integrante de si mesma. As proposições simples são
geralmente designadas por letras minúsculas p, q, r, s ..., chamadas letras
proposicionais.
Exemplo:
p : Oscar é prudente;
q : Mário é engenheiro;
r : Maria é morena.
Composta ou Molecular - é a proposição formada pela combinação de
duas ou mais proposições. São habitualmente designadas por letras
maiúsculas P, Q, R, S ..., também denominadas letras proposicionais.
Exemplo:
P : Walter é engenheiro E Pedro é estudante;
Q : Mauro é dedicado OU Pedro é trabalhador;
R : SE Flávio é estudioso ENTÃO será aprovado.
Conectivos
Definição: Palavras utilizadas para formar novas proposições a partir de outras.
Exemplos:
P: É dia ou é noite
Q: Não está chovendo
R: Se Jorge é engenheiro, então sabe matemática
S: O número 6 é par e 8 é um cubo perfeito
T: O triângulo ABC é eqüilátero se e somente se for eqüiângulo
Os conectivos utilizados acima foram “ou”, “não”, “se...então”, “e” e “... se e somente se...”.
Notação
O valor lógico de uma proposição simples p indica-se por V(p). Assim indica-se que p é
verdadeira por V(p)=V. De maneira análoga, exprimi-se que p é falsa por V(p)=F.
Exemplos
p: O sol é verde
q: Um quadrado tem 4 lados
V(p)=F; V(q)=V; V(r)=F; V(s)=V.
r: A moeda do Brasil é o dólar
s: 4 é raiz da equação x2-3x-4=0
6
Operadores
Negação
Chama-se negação de uma proposição p a proposição representada por
“não p”, cujo valor lógico é verdadeiro quando p é falsa e falso quando p é
verdadeiro. Simbolicamente, a negação de p é indicada por “~p”, que se
lê “não p”.
Conjunção
Chama-se conjunção de duas proposições p e q a proposição
representada por “p e q”, cujo valor lógico é verdadeiro quando as
proposições p e q são ambas verdadeiras e falso nos demais casos.
Simbolicamente, a conjunção de proposições p e q é indicada por “p 
q”, que se lê “p e q”.
Disjunção
Chama-se disjunção de duas proposições p e q a proposição
representada por “p ou q”, cujo valor lógico é verdadeiro quando pelo
menos uma das proposições p e q é verdadeira e falso quando ambas
as preposições são falsas. Simbolicamente, a disjunção de proposições
p e q é indicada por “p  q”, que se lê “p ou q”.
p
~p
V
F
F
V
p
q
pq
V
V
V
V
F
F
F
V
F
F
F
F
p
q
pq
V
V
V
V
F
V
F
V
V
F
F
F
Operadores
Negação
Chama-se negação de uma proposição p a proposição representada por
“não p”, cujo valor lógico é verdadeiro quando p é falsa e falso quando p é
verdadeiro. Simbolicamente, a negação de p é indicada por “~p”, que se
lê “não p”.
Conjunção
Chama-se conjunção de duas proposições p e q a proposição
representada por “p e q”, cujo valor lógico é verdadeiro quando as
proposições p e q são ambas verdadeiras e falso nos demais casos.
Simbolicamente, a conjunção de proposições p e q é indicada por “p 
q”, que se lê “p e q”.
Disjunção
Chama-se disjunção de duas proposições p e q a proposição
representada por “p ou q”, cujo valor lógico é verdadeiro quando pelo
menos uma das proposições p e q é verdadeira e falso quando ambas
as preposições são falsas. Simbolicamente, a disjunção de proposições
p e q é indicada por “p  q”, que se lê “p ou q”.
p
~p
V
F
F
V
p
q
pq
V
V
V
V
F
F
F
V
F
F
F
F
p
q
pq
V
V
V
V
F
V
F
V
V
F
F
F
7
Operadores
Disjunção exclusiva
Chama-se disjunção exclusiva de duas proposições p e q a proposição
representada por “ou p ou q mas não ambos”, cujo valor lógico é verdadeiro
somente quando p é verdadeiro ou q é verdadeiro, mas não quando ambos
são verdadeiros, e falso quando ambas as preposições são verdadeiras ou
falsas. Simbolicamente, a disjunção exclusiva de proposições p e q é
indicada por “p  q”, que se lê “ou p ou q mas não ambos”.
p
q
pq
V
V
F
V
F
V
F
V
V
F
F
F
Condicional
Chama-se proposição condicional ou apenas condicional, uma proposição
representada por “se p então q”, cujo valor lógico é a falsidade no caso em
que p é verdadeira e q é falsa e verdadeiro nos demais casos.
Simbolicamente, a condicional de duas proposições p e q é indicada por
“pq”, que se lê de uma das duas formas:
i – p é condição suficiente para q
ii – q é condição necessária para p
Bicondicional
Chama-se proposição bicondicional ou apenas bicondicional, uma
proposição representada por “p se e somente se q”, cujo valor lógico é
verdadeiro quando p e q são ambas verdadeiras ou falsas, e é falso nos
demais casos. Simbolicamente, a bicondicional de duas proposições p e q
é indicada por “pq”, que se lê de uma das duas formas:
i – p é condição necessária e suficiente para q
ii – q é condição necessária e suficiente para p
p
q
pq
V
V
V
V
F
F
F
V
V
F
F
V
P
q
pq
V
V
V
V
F
F
F
V
F
F
F
V
8