VARIÁVEIS ALEATÓRIAS Dada uma experiência aleatória

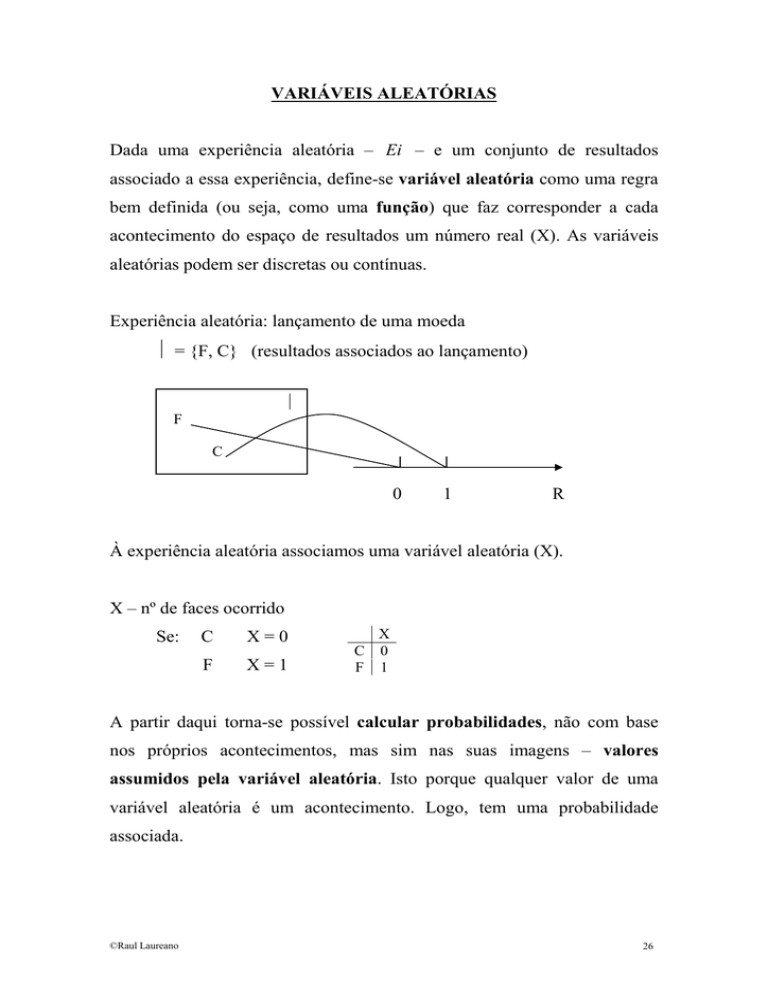
VARIÁVEIS ALEATÓRIAS
Dada uma experiência aleatória – Ei – e um conjunto de resultados
associado a essa experiência, define-se variável aleatória como uma regra
bem definida (ou seja, como uma função) que faz corresponder a cada
acontecimento do espaço de resultados um número real (X). As variáveis
aleatórias podem ser discretas ou contínuas.
Experiência aleatória: lançamento de uma moeda
Ω = {F, C} (resultados associados ao lançamento)
Ω
F
C
0
1
R
À experiência aleatória associamos uma variável aleatória (X).
X – nº de faces ocorrido
Se:
C
F
X=0
X=1
C
F
X
0
1
A partir daqui torna-se possível calcular probabilidades, não com base
nos próprios acontecimentos, mas sim nas suas imagens – valores
assumidos pela variável aleatória. Isto porque qualquer valor de uma
variável aleatória é um acontecimento. Logo, tem uma probabilidade
associada.
©Raul Laureano
26
Esquema do processo de construção do Modelo de Probabilidade
Experiência
aleatória
Espaço de
resultados
Listagem de todos
os resultados
Variável
aleatória
Atribuição de um
valor a cada
resultado
f(x)
Determinação da
probabilidade de
cada valor de X
X
Aplicação:
Considerando a experiência aleatória “controlo de qualidade” extraem-se,
de um vasto lote, três peças aleatoriamente e classifica-se cada uma das
peças em defeituosa (D) ou não defeituosa (N).
O espaço de resultados é:
Ω = { ( N , N , N ) ; ( N , N , D ) ; ( N , D , N ) ; ( N , D , D ) ; ( D , N , N ) ; ( D , N , D ) ; ( D , D , N ) ; ( D , D , D )}
Definindo, por exemplo, a variável aleatória:
X – número de peças defeituosas entre as três peças inspeccionadas.
A variável aleatória (V.A.) X tem como domínio Ω e como
contradomínio
{0,1, 2,3} .
Temos, portanto, uma variável aleatória
unidimensional e discreta (o seu contradomínio é um conjunto discreto,
isto é, finito ou infinito numerável).
©Raul Laureano
27
Considerando que 5 em cada 100 peças inspeccionadas são defeituosas,
podemos calcular as probabilidades:
P  X = 0  , P  X = 1 , P  X = 2  e P  X = 3 .
X
Ω
ℝ
(N,N,N )
( N ,N ,D)
0
Probabilidade
0,857375
( N , D, N )
( D, N , N )
( D, D, N )
1
0,135375
( D, N , D )
( N , D, D )
2
0,007125
( D, D, D )
3
0,000125
Cálculo da probabilidade condicional recorrendo à árvore de resultados:
N
(0,95)
N
(0,95)
N
(0,95)
D
(0,05)
0,95 x 0,95 x 0,95 = 0,857375
D
(0,05)
0,95 x 0,95 x 0,05 = 0,045125
N
(0,95)
0,95 x 0,05 x 0,95 = 0,045125
D
(0,05)
0,95 x 0,05 x 0,05 = 0,002375
N
(0,95)
D
(0,05)
N
(0,95)
D
(0,05)
0,05 x 0,95 x 0,95 = 0,045125
D
(0,05)
0,05 x 0,95 x 0,05 = 0,002375
N
(0,95)
0,05 x 0,05 x 0,95 = 0,002375
D
(0,05)
0,05 x 0,05 x 0,05 = 0,000125
©Raul Laureano
28
Assim,
P  X = 0  = 0,857375
probabilidade da V.A. X assumir o valor
zero (probabilidade de ter zero defeituosas)
P  X = 1 = 0,135375
P  X = 2  = 0, 007125
P  X = 3 = 0, 000125
A função de probabilidade da V.A. discreta X, que assume valores
x1 , x2 ,..., xn ,... , é representada por f ( x ) :
f ( x) =
P  X
 



0

= x 
se x = x j
j = 1, 2,..., n,...
se x ≠ x j
ou na forma tabular
x1
P  X = x1 
x
f ( x)
x2
P  X = x2 
...
...
xn
P  X = xn 
A função de probabilidade tem, pois, domínio ℝ e conjunto de chegada
 0,

1 e satisfaz as seguintes propriedades:
• 0 ≤ f ( x) ≤ 1
• sendo uma V.A. discreta finita
n
∑
j =1
n
( ) ∑ P  X = x j  = 1
j =1
f xj =
• sendo uma V.A. discreta infinita
∞
∞
∑ ( ) ∑ P  X = x j 
j =1
j =1
f xj =
©Raul Laureano
será uma série convergente de soma 1
29
Pode-se definir uma outra função – função de distribuição1 de uma
variável aleatória – como:
F ( x ) = P  X ≤ x 
A função distribuição tem, pois, domínio ℝ e conjunto de chegada  0, 1
e satisfaz as seguintes propriedades:
• 0 ≤ F ( x ) ≤ 1 , ∀x ∈ ℝ
F corresponde a uma probabilidade
• F ( x2 ) ≥ F ( x1 ) , ∀x1 , x2 com x2 > x1 F é monótona não decrescente
•
lim F ( x ) = 0
x →−∞
• lim F ( x ) = 1
x →∞
• P  x1 < X ≤ x2  = F ( x2 ) − F ( x1 ) , ∀x1 , x2 com x2 > x1
1
Frequentemente a função distribuição é também designada por função de probabilidade acumulada.
©Raul Laureano
30
No exemplo das peças defeituosas tem-se:
F ( 0 ) = P  X ≤ 0  = P  X = 0  = 0,857375
F (1) = P  X ≤ 1 = P  X = 0  + P  X = 1 = 0,99275
F ( 2 ) = P  X ≤ 2  = P  X ≤ 1 + P  X = 2  = 0,999875
F ( 3) = P  X ≤ 3 = 1
ou
F ( x) =
0



 0,857375



 0, 999875


 1
x<0
0 ≤ x <1
1≤ x < 2
x≥3
Representações gráficas das funções de probabilidade e de distribuição de
V.A. discretas:
Função de probabilidade: Y = f ( x )
f(x)
,9
Função de distribuição: y = F ( x )
F(x)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0 1 2 3
©Raul Laureano
x
0 1 2 3
x
31
Nas variáveis aleatórias contínuas X assume um número infinito de
valores pelo que não faz sentido falar da função de probabilidade – a
probabilidade de um ponto é sempre nula.
Então surge a função densidade de probabilidade (f.d.p.) de X, que tem
subjacente as probabilidades não nulas de intervalos ou, então, a taxa
instantânea de variação da probabilidade, definida por:
P  a < x ≤ b  =
b
∫a f ( x ) dx
o integral2 da f.d.p. entre os valores a e b
permite determinar P  a < x ≤ b  3
Note-se que a f.d.p., f ( x ) , corresponde, por analogia, ao polígono de
frequências relativas (de uma variável contínua) quando o número de
observações e o número de classes aumentam (e, portanto, diminui a
amplitude das classes). Desta forma, no limite, o polígono transforma-se
numa curva cuja equação define a f.d.p..
2
O integral é representado pelo símbolo
∫
e corresponde a uma função matemática que define a área
entre dois pontos de uma função. Como referem Maroco e Bisbo (2003), o integral é equivalente ao
somatório para as variáveis discretas e, por abuso, pode interpretar-se como sendo a soma de todos os
valores da função num determinado intervalo.
3
P [ a ≤ x ≤ b] = P [ a < x < b] + P [ x = a ] + P [ x = b] = P [ a < x < b] = P [ a ≤ x < b] .
©Raul Laureano
32
A f.d.p. verifica as propriedades:
• f (x) ≥ 0
•
não negatividade
∞
∫−∞ f ( x ) dx = 1
o integral em todo o domínio é 1
A função densidade de probabilidade (f.d.p.) corresponde à derivada da
função distribuição - F ( x ) , isto é,
f ( x) =
dF ( x )
, se a função de distribuição for derivável.
dx
A função de distribuição de uma V.A. contínua corresponde a:
F ( x ) = P  X ≤ x  =
x
∫−∞ f ( u ) du
4
E verifica as seguintes propriedades:
• É uma função contínua
• Se x < y , então F ( x ) ≤ F ( y ) , função crescente (em sentido lato)
• F ( −∞ ) = lim F ( x ) = 0
x →−∞
• F ( ∞ ) = lim F ( x ) = 1
x →∞
• P  a < x ≤ b  = F ( b ) − F ( a ) =
b
∫a f ( x ) dx
4
Como no integral o limite superior da integração é x , considera-se uma variável de integração diferente
de x , neste caso a variável u .
©Raul Laureano
33
Representações gráficas das funções densidade de probabilidade e de
distribuição de V.A. contínuas:
Função de distribuição: y = F ( x )
1
F(b)
F(a)
Função densidade de probabilidade: Y = f ( x )
Cálculo da probabilidade: P  a < x ≤ b  = F ( b ) − F ( a ) =
©Raul Laureano
b
f ( x ) dx
∫
a Recorrendo a
F( x )
Recorrendo a
f(x)
34
PARÂMETROS DAS VARIÁVEIS ALEATÓRIAS
Para se caracterizar, de uma forma reduzida, uma variável aleatória
(distribuição associada à população, definida pelas funções de distribuição
e de probabilidade, se discreta, e densidade de probabilidade, se contínua)
pode-se recorrer a algumas medidas (parâmetros).
Assim, as funções associadas às variáveis aleatórias podem ser
consideradas como representações de populações, ou sejam, evidenciam a
forma como os elementos de uma população de distribuem. De outra
forma, pode-se considerar que a função de probabilidade (ou a função
densidade de probabilidade) constitui um modelo para a representação da
distribuição dos elementos da população.
Os parâmetros5 mais comuns são:
• Valor esperado (ou esperança matemática ou média);
• Variância (ou variância esperada) e desvio-padrão;
• E quando se tem duas variáveis aleatórias, para analisar a relação entre
elas recorre-se às medidas de associação:
o Covariância;
o Coeficiente de correlação linear.
5
Recorde-se que as distribuições de frequências podem ser caracterizadas por estatísticas (números que
calculados com base em amostras sintetizam a configuração das distribuições e que variam de amostra
para amostra). No caso das variáveis aleatórias recorre-se a um conjunto de números (parâmetros, que são
fixos) para caracterizar as distribuições associadas às populações.
Podem-se calcular outros parâmetros, como sejam, a mediana e a moda. Verifica-se a existência de uma
correspondência entre as designações das estatísticas e dos parâmetros, podendo, em algumas situações,
acrescentar-se à designação, no caso das estatísticas, as palavras amostral ou da amostra, e, no caso dos
parâmetros, as palavras populacional ou da população.
©Raul Laureano
35
VALOR ESPERADO DE X – é um parâmetro de localização, representa-se por E  X  (ou por µ x ou por µ ) e, quando existe, define-se por:
• Se X é uma V.A. discreta
E  X  =
• Se X é uma V.A. contínua
E  X  =
n
∑ xi . f ( xi )
i =1
+∞
∫−∞ x . f ( x ) dx
VARIÂNCIA DE X – é um parâmetro de dispersão, representa-se por
VAR  X  (ou por σ2 x ou por σ2 ). A variância corresponde à média do
quadrado dos desvios em relação ao valor esperado:
(
VAR  X  = E  ( X − µ )2  = E  X 2  − E  X 




• Se X é uma V.A. discreta
VAR  X  =
• Se X é uma V.A. contínua
VAR  X  =
)
2
e define-se por:
n
∑ ( xi − µ )2 . f ( xi )
i =1
+∞
2
∫−∞ ( x − µ) . f ( x ) dx
Note-se que E  X 2  é dado por:


• Se X é uma V.A. discreta
E  X 2 


• Se X é uma V.A. contínua
E  X 2  =


=
n
∑ xi2 . f ( xi )
i =1
+∞ 2
∫−∞ x . f ( x ) dx
DESVIO-PADRÃO DE X – é um parâmetro de dispersão, representa-se
por σ (ou por σ x ). O desvio-padrão corresponde à raiz quadrada positiva
da variância, isto é, σ = + VAR  X  .
©Raul Laureano
36
Propriedades do valor esperado ( k , a e b são constantes e X e Y são duas
variáveis aleatórias - V.A.):
• E  k  = k - o valor esperado de uma constante k é a própria constante;
• E  kX  = k . E  X  - o valor esperado do produto de uma constante por
uma V.A. é igual ao produto da constante pelo valor
esperado da V.A.;
• E  aX + b  = a . E  X  + b - o valor esperado do produto de uma
constante por uma V.A. mais uma constante
é igual ao produto da constante pelo valor
esperado da V.A. mais a outra constante
(transformação linear);
• E  X ± Y  = E  X  ± E Y  - o valor esperado da soma algébrica de duas
V.A.
é
igual
à
soma
algébrica
dos
respectivos valores esperados;
• E  X .Y  = E  X  . E Y 
- se
X e Y forem independentes, o valor
esperado do produto de duas V.A. é igual ao
produto dos respectivos valores esperados.
Se
X eY
não
forem
independentes
E  X .Y  = E  X  . E Y  + cov ( X ,Y ) .
• E  g ( x )  =
©Raul Laureano








∑ g ( xi ) f ( xi )
se X discreta
i
+∞
∫-∞ g ( x ) f ( x ) dx
se X contínua
- valor esperado de uma
função de X
37
Propriedades da variância ( k , a e b são constantes e X e Y são duas V.A.):
• VAR  X  ≥ 0 ;
• Se VAR  X  = 0 então P  X = E  X   = 1;


• VAR  k  = 0 ;
• VAR  kX  = k 2 . VAR  X  ;
• VAR  aX ± b  = a 2 . VAR  X  ;
• VAR  X ± Y  = VAR  X  + VAR Y  ± 2. cov ( X ,Y )
-
Se
X e Y forem
independentes, então cov ( X ,Y ) = 0 (o recíproco não é verdadeiro);
Note-se que:
Se X é uma V.A. de média µ e variância σ2 então a V.A. W =
X −µ
σ
tem parâmetros: E W  = 0 e VAR W  = 1 .
Operando com as propriedades do valor esperado verifica-se que a variância
(VAR  X  ) pode ser obtida por:
(
)
2
VAR  X  = E  ( X − µ )2  ou VAR  X  = E  X 2  − E  X  .




2
2
E  ( X − E  X  )  = E  X 2  − 2 . X . E  X  + ( E  X  ) =




2
= E  X 2  + E  ( E  X  )  − 2 . E  X  . E  X  =




= E  X 2  + ( E  X  ) − 2 . ( E  X  )


2
= E  X 2  − ( E  X  )


2
=
2
em que:
X – variável;
E  X  – média;
quadrado; E  ( X − E  X  )

©Raul Laureano
2

( X − E  X  )
– desvio; ( X − E  X  )
2
– desvio
– média do desvio quadrado e E[X 2 ] = ∑ Xi 2 .P(Xi) .
k
i =1
38
COVARIÂNCIA – é uma medida de distribuição conjunta de X e Y , em
termos dos desvios face às respectivas médias. A covariância descreve a
relação linear entre duas variáveis e é dada por:
(

)(
cov ( X ,Y ) = E  X − E  X  . Y − E Y 
)  = E  XY  − E  X  . E Y 
COEFICIENTE DE CORRELAÇÃO LINEAR – descreve a relação
linear entre duas variáveis e tem a vantagem, em relação à covariância, de
ser independente da unidade de medida em que as variáveis estão
expressas.
ρ XY =
cov ( X ,Y )
VAR  X  . VAR Y 
Verifica-se que −1 ≤ ρ ≤ 1 .
O coeficiente de correlação indica o sentido da relação linear, relação
directa ou positiva (sinal +) ou inversa ou negativa (sinal -), e a intensidade,
quanto mais perto do 1 (relação perfeita), em valor absoluto, for o
coeficiente mais forte é a relação e quanto mais perto do 0 (ausência de
relação) mais fraca é a relação entre as duas variáveis.
©Raul Laureano
39
APLICAÇÃO:
Suponha que temos uma experiência aleatória que consiste no lançamento
sucessivo de duas moedas (não viciadas). Pretende-se saber qual o número
esperado de faces que irá ocorrer.
Passos a dar:
1º) Definir o espaço de resultados
Experiência aleatória – lançamento sucessivo de 2 moedas
Ω = {(F,F); (F,C); (C,F); (C,C)}
2º) Definir a variável aleatória
X – número de faces ocorrido
Se tivermos o resultado: (F,F)
X=2
(F,C) ou (C,F)
X=1
(C,C)
X=0
3º) Determinar a probabilidade de cada valor de X. Ou seja, constrói-se um
quadro em que a cada valor de X se faz corresponder a sua
probabilidade de ocorrência. A este quadro chama-se quadro de
distribuição de probabilidade de X, ou função de probabilidade de
X, que se representa por P ( xi ) ou f ( xi ) e deve satisfazer duas
condições:
• P ( xi ) ≥ 0 , ∀xi
•
©Raul Laureano
n
∑ P(xi ) = 1
i =1
40
Então, a função de probabilidade P ( xi ) é:
xi
P ( xi )
0
1
2
¼
2/4 = ½
¼
Facilmente se vê que P ( xi ) satisfaz as duas condições:
• P ( xi ) ≥ 0 para i = 0,1, 2 ;
•
2
∑ P ( xi ) =
i =0
1 + 2 + 1 =1
4
4
4
4º) Finalmente, pode calcular-se o valor esperado de X , ou seja, o número
de faces que, em média, se espera que ocorra.
O valor esperado de uma variável aleatória é uma medida que, de
forma sintética, dá informação relevante sobre o seu comportamento.
O valor esperado de uma variável aleatória X , que se representa por
E  X  , define-se como a média dos valores assumidos por X
ponderados pela respectiva probabilidade.
E  X  =
n
∑ x i .P(x i )
i =1
com
P ( xi ) ≥ 0 , ∀xi
n
∑ P(xi ) = 1
i =1
©Raul Laureano
41
Calcule-se o número esperado de faces a ocorrer (valor esperado):
xi
P ( xi )
0
1
2
¼
½
¼
E  X  =
x i .P(x i )
0
½
½
1
2
∑ x i .P(xi ) = 0 ×
i =0
1 + 1× 1 + 2 × 1 = 1
4
2
4
Assim, em termos médios, espera-se que no lançamento sucessivo de
duas moedas ocorra uma face.
5º) Para além do valor esperado, podemos também calcular, como medida
sintetizadora e auxiliar, a variância esperada (média do quadrado dos
desvios em relação ao valor esperado).

(
VAR  X  = E  X − E  X 


)
2



Xi
P ( Xi )
Xi . P ( Xi )
Xi 2 . P ( Xi )
0
1
2
1/4
1/2
1/4
0
1/2
1/2
1
0
1/2
1
3/2
então,
VAR  X  = E  X 2  − ( E  X  )


©Raul Laureano
2
=
3
1
− 12 =
2
2
42
VALOR ESPERADO: Outros exemplos
O conceito de valor esperado tem a sua origem nos jogos do acaso.
Exemplo 1:
No lançamento de um dado, não viciado, recebe-se um euro se sair número
par, perdem-se dois euros se sair 1 ou 3 e ganham-se três euros se ocorrer o
5.
A questão que se levanta é a de saber se vale a pena participar num jogo
com estas condições. De outro modo, quanto é que se pode ganhar?
Sabe-se que o espaço de resultados da experiência aleatória é:
Ω = {1, 2, 3, 4, 5, 6}
A probabilidade de cada resultado individual, sendo o dado não viciado
será P [Wi] = 1/6
1€ se ocorrer
2
4
6
3 € se ocorrer
5
2 € se ocorrer
1
3
Ganha-se
Perde-se
A questão para a qual se pretende obter resposta é de saber, em termos
médios quanto se espera ganhar? Para obter a resposta basta fazer a média
ponderada dos valores a perder ou receber. O coeficiente de ponderação é
dado pela probabilidade de ocorrência de cada um desses valores.
Representando o ganho por G, tem-se:
P [G = 1] = 3/6
P [G = 3] = 1/6
P [G = -2] = 2/6
Então, o valor esperado do ganho que se representa por E [G] virá:
E [G] = 1 . 1/2 + 3 . 1/6 + (-2) . 1/3 = 0,3(3) euros
©Raul Laureano
43
Note-se que este valor não é uma quantia que efectivamente se receba, mas
indica se o jogo é ou não favorável ao jogador. Se o valor esperado do
ganho fosse negativo o jogador concluiria que em termos médios perdia
mais do que se ganhava. Para participar no jogo, o jogador geralmente
entra com uma certa quantia. Representando por E a entrada, diz-se que o
jogo é equitativo, isto é, que não favorece nenhuma das partes se:
E [E] = E [G]
isto é, E [L] = 0
(i.e. o valor esperado do lucro), sendo L = G - E
Exemplo 2:
Suponha que entra numa livraria para comprar um livro que custa 36 euros.
Tem na carteira quatro notas de 10 euros e uma de 50 euros. O livreiro
propõe-lhe o pagamento com uma nota tirada ao acaso da carteira. Quem
poderia ficar favorecido?
− porque o livro custa 36 euros
E [G] = 36
− porque o comprador tem cinco notas, quatro de 10 e uma de 50 euros
E
Probabilidade

E [E] = 10  4
 5



+ 50
10
4/5



1
5



50
1/5
= 18 euros
− então, o jogo não é equitativo e favorece o comprador
©Raul Laureano
E [E] ≠ E [E]
(18 ≠ 36)
E [E] < E [G]
(18 < 36)
44
DISTRIBUIÇÕES TEÓRICAS MAIS IMPORTANTES
Existem alguns modelos probabilísticos (distribuições teóricas) que são
correntemente adaptáveis a um vasto conjunto de fenómenos aleatórios que
ocorrem no dia-a-dia.
As distribuições empíricas (ou distribuições de frequências) de variáveis,
discretas ou contínuas, com que se deparam frequentemente os
investigadores nos estudos empíricos, podem ser, muitas vezes,
representadas por distribuições teóricas que se ajustam ao comportamento
dessas variáveis aleatórias. Deste modo, também as distribuições teóricas
se dividem em distribuições discretas e em distribuições contínuas.
As principais distribuições discretas são:
• Distribuição uniforme;
• Distribuição binomial;
• Distribuição binomial negativa;
• Distribuição hipergeométrica;
• Distribuição de Bernoulli;
• Distribuição multinomial;
• Distribuição geométrica ou de
Pascal;
• Distribuição de Poisson.
As principais distribuições contínuas são:
• Distribuição uniforme;
• Distribuição exponencial;
• Distribuição normal e normal
padrão (ou estandardizada);
• Distribuição Gama.
Uma vez que são correntemente utilizados e para evitar o contínuo recurso
às funções de probabilidade, no caso das distribuições discretas, e às
funções densidade de probabilidade, nas distribuições contínuas, ou, ainda,
às funções de distribuição foram elaboradas tabelas estatísticas – tabelas
probabilísticas – (disponíveis em quase todos os livros de estatística) de
forma a facilitar os cálculos das probabilidades (sem ter, portanto, que
recorrer-se directamente às referidas funções).
©Raul Laureano
45
DISTRIBUIÇÕES TEÓRICAS DE VARIÁVEIS ALEATÓRIAS
DISCRETAS
DISTRIBUIÇÃO DE BERNOULLI
Prova de Bernoulli
Admita-se uma experiência aleatória com apenas dois resultados:
• A – sucesso, com P  A  = p
• A – insucesso, com P  A  = 1 − p = q


Este tipo de experiência aleatória designa-se por prova de Bernoulli
Sucessão de provas de Bernoulli: processo caracterizado por repetidas
provas nas seguintes condições:
1. Em cada prova só existem dois resultados possíveis (e mutuamente
exclusivos): sucesso e insucesso;
2. A probabilidade de sucesso, p , mantém-se constante de prova para
prova. A probabilidade de insucesso designa-se por q = 1 − p ;
3. As provas são independentes, ou seja, os resultados obtidos numa
certa prova ou sequência de provas não influenciam os resultados das
provas subsequentes.
©Raul Laureano
46
Distribuição de Bernoulli
Tem-se uma única prova de Bernoulli e define-se X com apenas dois
valores: 0 se insucesso e 1 se sucesso.
E tem-se que P  X = 1 = p e P  X = 0  = q = 1 − p .
Então, a V.A. X segue uma distribuição de Bernoulli se a sua função de
probabilidade for dada por:
1− x
f ( x ) = p x (1 − p )
,
x = 0,1
E, consequentemente, a função de distribuição ser dada por:
F ( x) =
0



1 −


1

x<0
p=q
0 ≤ x <1
x ≥1
E o valor esperado e a variância, são dados por:
• E  X  = p
• VAR  X  = p (1 − p ) = p.q
Diz-se que X, nestas condições, segue uma distribuição de Bernoulli de
parâmetro p e escreve-se X
©Raul Laureano
Bern ( p ) . Note-se que 0 ≤ p ≤ 1.
47
Exemplo 1:
X = número de 6 no lançamento de um dado perfeito, ganhando-se se sair
6. Assim, X representa o número de vitórias obtidas num lançamento do
dado.
X ∼ Bern ( p
f (1) =




1
6
1




=
1
6

. 1 −

)
1
6
1−1




= 1
6
E  X  = 1
6
F (1) = 1
VAR  X  = 1 × 5 = 5
6
6
36
Exemplo 2:
Considerando o lançamento aleatório de um dado 10 vezes e uma vitória se
sair um número superior 4.
Assim, a probabilidade de sucesso é p = 2 = 1 e, consequentemente, a
6
3
probabilidade de insucesso é q = 1 − p = 1 − 1 = 2 .
3
3
Está-se, pois, na presença de um processo de Bernoulli em que a prova se
repete 10 vezes, cada prova tem dois resultados possíveis (sucesso e
insucesso), a probabilidade de sucesso é igual em todas as provas e o
resultado de uma prova não vai afectar o resultado da prova seguinte (os
lançamentos são independentes).
©Raul Laureano
48
DISTRIBUIÇÕES TEÓRICAS DE VARIÁVEIS ALEATÓRIAS
CONTÍNUAS
DISTRIBUIÇÃO UNIFORME
Uma variável aleatória contínua segue uma distribuição uniforme quando a
sua função densidade de probabilidade é constante em todo o intervalo
a , b


e nula fora desse intervalo.
Assim, a função densidade de probabilidade é dada por:
f (x) =








1
b−a
0
se a ≤ x ≤ b
se x < a ou x > b
E a sua função de distribuição por:
F ( x) =
x
∫−∞ f ( u ) du =
0


 x

 b


 1
se x < a
−a
−a
se a ≤ x ≤ b
se x > b
O valor esperado e a variância, são dados por:
•
E  X  = a + b
2
• VAR  X  =
(b − a)
2
12
Diz-se que a V.A. X, nestas condições, segue uma distribuição uniforme
em  a , b  e escreve-se X ∩ U ( a , b ) .
©Raul Laureano
49
Representações gráficas de X ∩ U ( a , b ) :
• Função densidade de probabilidade
f ( x)
1
b−a
0
a
b
x
b
x
• Função de distribuição
F( x)
1
0
a
Exemplo (adaptado de Guimarães e Cabral, 1997, p.195):
Considere que o atraso (expresso em minutos) nas chegadas à estação de
uma cidade, dos comboios directos provenientes de outra cidade, segue
uma distribuição U ( 0 ,12 ) .
Qual a probabilidade de ocorrer um atraso compreendido entre os 5 e os 10
minutos?
P  5 ≤ x ≤ 10  = F (10 ) − F ( 5 ) =
P  5 ≤ x ≤ 10  =
10 − 0
5−0
10
5
5
−
=
−
=
= 0, 416
12 − 0
12 − 0
12
12
12
1. (10 − 5 )
5
=
= 0, 416
12 − 0
12
Em média, qual o atraso que se espera que ocorra na chegada à estação?
µ = E  X  =
©Raul Laureano
0 + 12
12
=
= 6 minutos
2
2
50
DISTRIBUIÇÃO NORMAL
Existe uma grande variedade de fenómenos na vida real que obedecem a
uma distribuição normal ou que se aproximam de forma significativa da
distribuição normal. Assim, esta distribuição assume especial relevância
quando se está na presença variáveis aleatórias contínuas, isto é, que podem
assumir um conjunto infinito não numerável de valores.
Realce-se que a importância desta distribuição ainda é mais acrescida pois,
mediante a verificação de certas condições, certas distribuições de variáveis
aleatórias discretas, tais como a distribuição binomial e a de Poisson,
podem ser aproximadas à distribuição normal.
Diz-se que uma V.A. X segue uma distribuição normal6 se a sua função
densidade de probabilidade for dada por7:
f ( x) =
1
2 πσ2
 x −µ
− 1 
.e 2  σ




2
, x ∈ ] − ∞ ; + ∞[
representando µ (miu) a média ( −∞ < µ < +∞ ) e σ (sigma) o desvio-padrão ( σ > 0 ).
E, consequentemente, se a função de distribuição for dada por8:
F ( x) =
 t −µ 

− 1 
x
1
2  σ  dt
e
∫
2 πσ2 −∞
6
Também designada por distribuição Gaussiana (ou de Gauss), em homenagem ao matemático alemão
Carl Gauss.
7
Recorde-se que e corresponde ao número de Napier e que e = 2 , 7182818... . Por sua vez, o π (pi)
tem o valor de π = 3,141519265... .
8
A função de distribuição não é integrável analiticamente, ou seja, não é possível determinar
explicitamente a sua primitiva, pelo que não se obtém uma expressão algébrica para os valores desta
função, sendo estes calculados por via numérica.
©Raul Laureano
51
O valor esperado e a variância são dados por:
•
E  X  = µ
• VAR  X  = σ2
Diz-se que a V.A. X, nestas condições, segue uma distribuição normal
de parâmetros caracterizadores µ e σ e escreve-se X ∩ n ( µ ; σ ) .
Representações gráficas de X ∩ n ( µ , σ ) :
• Função densidade de probabilidade (curva normal)
f ( x)
x
Fonte: Adaptado de Guimarães e Cabral (1997, p.199)
• Função de distribuição
F(x)
x
Fonte: Adaptado de Guimarães e Cabral (1997, p.199)
©Raul Laureano
52
Propriedades e características:
• É uma das distribuições mais utilizadas;
• A função densidade de probabilidade tem forma de sino e é unimodal
(um só máximo, correspondendo a x = µ );
• A função densidade de probabilidade é simétrica em torno da sua média.
Assim, a média é igual à mediana e igual à moda ( µ = Me = Mo );
• A função densidade de probabilidade tem pontos de inflexão para
x = µ ± σ e aproxima-se assimptoticamente do eixo das abcissas, ou
seja, lim f ( x ) = 0 ;
x →±∞
©Raul Laureano
53
• Quaisquer que sejam os parâmetros ( µ e σ ) da distribuição normal
verifica-se que existe uma proporção de observações constante (área
definida pela f.d.p.) entre a média e ± k desvios-padrão.
Para os intervalos µ ± σ , µ ± 2 σ e µ ± 3σ tem-se:
68,3%
µ
95,5%
µ
99,7%
µ
Fonte: Adaptado de Ramos (2004)
• A distribuição normal é adequada para caracterizar muitos fenómenos
físicos (pesos, …) e descreve bem a distribuição dos erros de medição,
para além de muitas outras aplicações em que é utilizada.
©Raul Laureano
54
• Qualquer transformação linear de uma V.A. com distribuição normal
resulta numa variável também com distribuição normal:
(
Se X ∩ n ( x ; µ ; σ ) então9 X '∩ n x ' = ax + b ; µ ' = aµ + b ; σ ' = a 2 σ2
)
em que a e b são constantes e a ≠ 0 ;
• Aditividade da distribuição normal:
Tendo
k
V.A.
Xi ∩ n ( µi ; σi ) então a variável T =
normal: T =
Xi ( i = 1, 2, 3,..., k ) ,
independentes
k
∑ ai Xi ∩
i =1

n 
i

k
que
k
∑ ai Xi
segue uma distribuição
k

i =1
∑ ai µi ; ∑
=1
em
i =1
ai2 .σi2 


Deste modo, conclui-se que:
o Sk = X1 + X 2 + ... + X k =
∑ Xi ∩ n ( k .µ ; σ.
k
i =1






o X1 + X 2 ∩ n  µ1 + µ2 ; σ12 + σ22

)
k ;
e
X1 − X 2 ∩ n  µ1 − µ 2 ; σ12 + σ22  ;


k
∑ Xi
o com X = i =1
k
9

se tem X ∩ n  µ ; σ
k


.


Recorde-se as propriedades do valor esperado e da variância: E [ aX + b ] = a . E [ X ] + b e
VAR [ aX + b ] = a 2 . VAR [ X ] .
©Raul Laureano
55
Cálculo das probabilidades de uma V.A. com distribuição normal
Uma vez que os parâmetros da distribuição normal, quer a média, quer o
desvio-padrão, podem assumir uma infinidade de valores não numeráveis,
torna-se impossível apresentar tabelas estatísticas para cada combinação
dos dois parâmetros.
Assim, recorre-se à chamada distribuição normal padrão (ou normal
reduzida, ou normal standard) para calcular as probabilidades de uma
variável aleatória X .
Assim, se X ∩ ( µ ; σ ) então a variável Z =
X −µ
(obtida a partir de X ,
σ
quaisquer que sejam os seus parâmetros) tem distribuição normal de
parâmetros 0 e 1, respectivamente, para a média e para o desvio-padrão.
Z =
X −µ
∩ n ( 0 ; 1)
σ
A variável aleatória contínua Z designa-se por variável estandardizada,
reduzida ou normal-padrão.
Apenas a função de distribuição F ( z ) = P  Z ≤ z  da distribuição normal-padrão se encontra tabelada10 e, usualmente, apenas para valores positivos
de Z , com 0 ≤ z ≤ 3, 49 , sendo que as probabilidades para os valores
negativos de Z são calculadas tendo em conta a simetria da distribuição
normal.
10
F(Z)
Para
=
a
z
∫ −∞
distribuição
1
−
normal-padrão
tem-se
que
f (z) =
1
2π
.e
−
z2
2
e
t2
2
dt . É usual representar a função densidade de probabilidade por φ (phi
.e
2π
minúsculo) e a função de distribuição por Ф (phi maiúsculo).
©Raul Laureano
56
O Excel disponibiliza as funções NORMDIST e NORMSDIST, para o cálculo das
probabilidades, respectivamente, de uma variável com distribuição normal e de uma
com distribuição normal-padrão:
=NORMDIST(x - nº para o qual se pretende a distribuição; µ – média da distribuição;
σ – desvio-padrão da distribuição; tipo de função). O argumento tipo de função deverá
ser um valor lógico, 0 para f ( x ) e, por exemplo, 1 para F ( x ) .
=NORMSDIST(z - nº para o qual se pretende a distribuição). Só calcula a função de
distribuição.
Paralelamente, o Excel disponibiliza as funções NORMINV e NORMSINV que
permitem determinar o valor para o qual se tem a distribuição, conhecida a respectiva
probabilidade acumulada, respectivamente, de uma variável com distribuição normal e
de uma com distribuição normal-padrão:
=NORMINV(F – probabilidade acumulada; µ – média da distribuição; σ – desvio-
-padrão da distribuição)
=NORMSINV(F – probabilidade acumulada)
Então, vejam-se os seguintes exemplos de cálculo de probabilidades:
• Se X ∩ n (15 ; 3) tem-se:

P  X ≤ 18  = P  X − 15 ≤ 18 − 15
3
3




= P  Z ≤ 1 = 0,8413
Note-se que o valor de Z = 1 significa que 18 se encontra
1 desvio-padrão acima da média (18 = 3 + 15)!
©Raul Laureano
z
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
0,00
0,5000
0,5398
0,5793
0,6179
0,6554
0,6915
0,7257
0,7580
0,7881
0,8159
0,8413
0,8643
0,8849
0,9032
0,01
0,5040
0,5438
0,5832
0,6217
0,6591
0,6950
0,7291
0,7611
0,7910
0,8186
0,8438
0,8665
0,8869
0,9049
57
0,02
0,5080
0,5478
0,5871
0,6255
0,6628
0,6985
0,7324
0,7642
0,7939
0,8212
0,8461
0,8686
0,8888
0,9066
• Se X ∩ n (100 ; 35 ) tem-se:

P  X < 100  = P  X − 100 < 100 − 100
35
35


P  X < 30  = P  Z < 30 − 100
35







= P  Z < 0  = 0,5
= P  Z < −2  = 1 − P  Z < 2  = 1 − 0, 9772 = 0, 0228

P  X > 150  = 1 − P  X ≤ 150  = 1 − P  Z ≤ 150 − 100
35




=
= 1 − P  Z ≤ 1, 4286  = 1 − P  Z ≤ 1, 43 = 1 − 0, 9236 = 0, 0764

P  60 < X < 140  = P  60 − 100 < Z < 140 − 100
35
35

(



= P  −1,14 < Z < 1,14  =
)
= P  Z < 1,14  − 1 − P  Z < 1,14  = 0,8729 − (1 − 0,8729 ) = 0, 7458

P  X ≥ 80  = P  Z ≥ 80 − 100
35

©Raul Laureano



= P  Z ≥ −0, 57  = P  Z ≤ 0, 57  = 0, 7157
58
Recorde-se:
• P  Z ≤ z  = P  Z < z  ;
• P  Z ≤ − z  = P  Z ≥ z  ;
• P  Z ≥ − z  = P  Z ≤ z  ;
• P  Z ≥ z  + P  Z ≤ z  = 1 ;
• P  Z ≤ − z  = 1 − P  Z ≤ z  ;
• P  Z ≥ z  = 1 − P  Z ≤ z  ;
• P  µ − σ < X < µ + σ  = P  µ − σ − µ < Z < µ − σ + µ

σ
σ

 =

P  −1 < Z < 1 ≈ 0, 68
• P  µ − 2 σ < X < µ + 2σ  = P  −2 < Z < 2  ≈ 0,95 ;
• P  µ − 3σ < X < µ + 3σ  = P  −3 < Z < 3 ≈ 0,99 ;
•
P [ Z < z ] = 0 , 3336
⇔
P [ Z > − z ] = 0 , 3336
⇔
P [ Z < − z ] = 1 − 0 , 3336
⇔
P [ Z < − z ] = 0 , 6664
pelo que consultando a tabela se obtém z : − z = 0, 43 ⇔ z = − 0, 43 ;
•
P [ Z < z ] = 0 , 9881 .
Pela tabela obtém-se z = 2, 26 ;
•
P [ Z > z ] = 0 , 484
⇔
P [ Z < z ] = 1 − 0 , 484
⇔
P [ Z < z ] = 0 , 516
pelo que consultando a tabela se obtém z = 0, 04 .
©Raul Laureano
59
BIBLIOGRAFIA CONSULTADA
Guimarães, Rui e Cabral, José (1997) Estatística, Edição Revista,
McGraw-Hill.
Maroco, João e Bispo, Regina (2003) Estatística aplicada às ciências
sociais e humanas, Manuais Universitários, Climepsi Editores.
Murteira, Bento, Ribeiro, Carlos, Silva, João e Pimenta, Carlos (2002)
Introdução à Estatística, McGraw-Hill.
Pedrosa, António e Gama, Sílvio (2004) Introdução Computacional à
Probabilidade e Estatística, Porto Editora.
Pinto, J. Carlos e Curto, J. (1999) Estatística para Economia e Gestão –
Instrumentos de Apoio à Tomada de Decisão, Edições Sílabo.
Ramos, Madalena (2004) Acetatos sobre Probabilidades e Distribuição
Normal para apoio às cadeiras de Estatística, ISCTE, não publicado.
Reis. Elizabeth, Melo, Paulo, Andrade, Rosa e Calapez, Teresa (2001)
Estatística Aplicada, Vol. 1, 4ª Edição Revista, Edições Sílabo.
Reis. Elizabeth, Melo, Paulo, Andrade, Rosa e Calapez, Teresa (2003)
Exercícios de Estatística Aplicada, Vol. 1, Edições Sílabo.
©Raul Laureano
60
TABELAS ESTATÍSTICAS
DISTRIBUIÇÃO NORMAL PADRÃO (OU REDUZIDA OU STANDARD)
(Função de distribuição)
X ∩ n ( µ = 0; σ = 1 )
F(Z )
= P[Z ≤ z] =
z
∫ −∞
1
2π
.e
−
t2
2
dt
z
0,0
0,1
0,2
0,3
0,4
0,00
0,5000
0,5398
0,5793
0,6179
0,6554
0,01
0,5040
0,5438
0,5832
0,6217
0,6591
0,02
0,5080
0,5478
0,5871
0,6255
0,6628
0,03
0,5120
0,5517
0,5910
0,6293
0,6664
0,04
0,5160
0,5557
0,5948
0,6331
0,6700
0,05
0,5199
0,5596
0,5987
0,6368
0,6736
0,06
0,5239
0,5636
0,6026
0,6406
0,6772
0,07
0,5279
0,5675
0,6064
0,6443
0,6808
0,08
0,5319
0,5714
0,6103
0,6480
0,6844
0,09
0,5359
0,5753
0,6141
0,6517
0,6879
0,5
0,6
0,7
0,8
0,9
0,6915
0,7257
0,7580
0,7881
0,8159
0,6950
0,7291
0,7611
0,7910
0,8186
0,6985
0,7324
0,7642
0,7939
0,8212
0,7019
0,7357
0,7673
0,7967
0,8238
0,7054
0,7389
0,7704
0,7995
0,8264
0,7088
0,7422
0,7734
0,8023
0,8289
0,7123
0,7454
0,7764
0,8051
0,8315
0,7157
0,7486
0,7794
0,8078
0,8340
0,7190
0,7517
0,7823
0,8106
0,8365
0,7224
0,7549
0,7852
0,8133
0,8389
1,0
1,1
1,2
1,3
1,4
0,8413
0,8643
0,8849
0,9032
0,9192
0,8438
0,8665
0,8869
0,9049
0,9207
0,8461
0,8686
0,8888
0,9066
0,9222
0,8485
0,8708
0,8907
0,9082
0,9236
0,8508
0,8729
0,8925
0,9099
0,9251
0,8531
0,8749
0,8944
0,9115
0,9265
0,8554
0,8770
0,8962
0,9131
0,9279
0,8577
0,8790
0,8980
0,9147
0,9292
0,8599
0,8810
0,8997
0,9162
0,9306
0,8621
0,8830
0,9015
0,9177
0,9319
1,5
1,6
1,7
1,8
1,9
0,9332
0,9452
0,9554
0,9641
0,9713
0,9345
0,9463
0,9564
0,9649
0,9719
0,9357
0,9474
0,9573
0,9656
0,9726
0,9370
0,9484
0,9582
0,9664
0,9732
0,9382
0,9495
0,9591
0,9671
0,9738
0,9394
0,9505
0,9599
0,9678
0,9744
0,9406
0,9515
0,9608
0,9686
0,9750
0,9418
0,9525
0,9616
0,9693
0,9756
0,9429
0,9535
0,9625
0,9699
0,9761
0,9441
0,9545
0,9633
0,9706
0,9767
2,0
2,1
2,2
2,3
2,4
0,9772
0,9821
0,9861
0,9893
0,9918
0,9778
0,9826
0,9864
0,9896
0,9920
0,9783
0,9830
0,9868
0,9898
0,9922
0,9788
0,9834
0,9871
0,9901
0,9925
0,9793
0,9838
0,9875
0,9904
0,9927
0,9798
0,9842
0,9878
0,9906
0,9929
0,9803
0,9846
0,9881
0,9909
0,9931
0,9808
0,9850
0,9884
0,9911
0,9932
0,9812
0,9854
0,9887
0,9913
0,9934
0,9817
0,9857
0,9890
0,9916
0,9936
2,5
2,6
2,7
2,8
2,9
0,9938
0,9953
0,9965
0,9974
0,9981
0,9940
0,9955
0,9966
0,9975
0,9982
0,9941
0,9956
0,9967
0,9976
0,9982
0,9943
0,9957
0,9968
0,9977
0,9983
0,9945
0,9959
0,9969
0,9977
0,9984
0,9946
0,9960
0,9970
0,9978
0,9984
0,9948
0,9961
0,9971
0,9979
0,9985
0,9949
0,9962
0,9972
0,9979
0,9985
0,9951
0,9963
0,9973
0,9980
0,9986
0,9952
0,9964
0,9974
0,9981
0,9986
3,0
3,1
3,2
3,3
3,4
0,9987
0,9990
0,9993
0,9995
0,9997
0,9987
0,9991
0,9993
0,9995
0,9997
0,9987
0,9991
0,9994
0,9995
0,9997
0,9988
0,9991
0,9994
0,9996
0,9997
0,9988
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9995
0,9996
0,9997
0,9990
0,9993
0,9995
0,9996
0,9997
0,9990
0,9993
0,9995
0,9997
0,9998
1,282
0,90
0,20
1,645
0,95
0,10
1,960
0,975
0,05
2,326
0,99
0,02
2,576
0,995
0,01
3,090
0,999
0,002
3,291
0,9995
0,001
3,891
4,417
0,99995 0,999995
0,0001 0,00001
z
F(z)
2 [1 - F(z) ]
©Raul Laureano
61