a interpretação geométrica e programas desenvolvidos no mathcad

A INTERPRETAÇÃO GEOMÉTRICA E PROGRAMAS
DESENVOLVIDOS NO MATHCAD PARA REFINAR RAÍZES DE
FUNÇÕES TRANSCENDENTES E POLINOMIAIS
RETZLAFF, Eliani – URI
[email protected]
CONTRI, Rozelaine de Fátima Franzin – URI
[email protected]
PRESTES, Rosangela Ferreira – URI
[email protected]
Eixo Temático: Comunicação e Tecnologia
Agência Financiadora: não contou com financiamento
Resumo
Este trabalho tem como proposta contribuir ao processo educativo, especificamente, no ensino
e aprendizagem de zeros de funções, com ênfase no uso de tecnologias, estudados na
disciplina de Cálculo Numérico, do curso de matemática. Para tal, foram efetuadas pesquisas
sobre conteúdo de zeros de funções polinomiais e transcendentes, que tinham como base a
interpretação geométrica, estudo de procedimentos para posterior construção de algoritmos e
elaboração de programas por meio do software Mathcad, cuja linguagem é própria. Com o
uso da tecnologia computador pode-se possibilitar os acadêmicos de cursos de graduação
desenvolverem a habilidade de organizar sequências de passos para utilização de diferentes
métodos numéricos para refinar raízes de funções, tornando possível avaliar a escolha do
método a ser utilizado, observando desde a facilidade da construção de gráficos até o processo
do programa e seus resultados, que são fornecidos sob a forma de tabela. O objetivo de
elaborar algoritmos dos principais métodos estudados, implementá-los em computador e fazer
aplicações é fornecer condições para que se possa conhecer, calcular, utilizar e aplicar os
métodos numéricos na solução de problemas reais, onde manualmente seria trabalhoso e de
difícil visualização gráfica, permitindo desta forma o uso adequado da ferramenta no ensino e
melhor análise de resultados calculados.
Palavras-chave: Zeros de funções, MathCad, Algoritmo, Programas, Interpretação
Geométrica.
7175
Introdução
Este trabalho justifica-se pelo fato de que o crescente uso e facilitado acesso da
ferramenta computador, onde diferentes linguagens de programação e softwares Matemáticos
com suas linguagens próprias são capazes de tornar possível resolver alguns entraves de apelo
de cálculos exaustivos e repetitivos necessários para resolução de problemas reais contendo
zeros de funções polinomiais e transcendentes, em que condições manuais não possibilitariam
sua prática e precisões. Cálculos repetitivos e extensos, estes, como os métodos numéricos
que são estudados na disciplina de Cálculo Numérico, ministrada no oitavo semestre da
graduação em Matemática, da URI campus de Santo Ângelo, usados para resolver problemas
aos quais não existem métodos analíticos ou são dados fornecidos por meio de tabelas, que
quando não utilizados os recursos computacionais podem diminuir sua aplicabilidade.
Desta forma, por meio do conteúdo zeros de funções, procurou-se entender os métodos
numéricos (Bisseção, Iteração Linear e Newton-Raphson) pela interpretação geométrica,
elaboração de algoritmos e execução de programas para desenvolver outras habilidades
matemáticas e assim permitir o uso adequado do software para o ensino e aprendizagem do
conteúdo em questão, bem como proporcionar um maior contato do licenciado em
Matemática para a solução de um problema real de forma que se utilize o software Mathcad,
que, não requer aprendizado demorado para o início da utilização e dentre outros, é o que
apresenta facilidade de plotar gráficos e as equações são apresentadas como se escreve no
papel.
Os programas elaborados têm o objetivo de automatizar a manipulação de cálculos
matemáticos, expressões, fórmulas e equações. Com relação a facilidade de elaboração de
rotinas computacionais, tem uma linguagem matemática associada que torna capaz de o
acadêmico relacionar melhor o programa a ser construído com o algoritmo. Também, torna-o
ferramenta para o cálculo numérico possibilitando resultar erros devido a suas características
intrínsecas, podendo quantificar os erros e encontrar formas de se não eliminá-los, minimizálos.
A Matemática e a Iteração com o Computador
Sabe-se que apenas conhecimentos gerais de informática não são o suficiente para o
uso adequado da tecnologia computador, eles devem ser acompanhados pelo domínio da
7176
informação, ou seja, que o indivíduo tenha a capacidade de reunir informações, avaliá-las e
tomar uma decisão fundamentada, pois os computadores representam um papel importante em
nossa sociedade, porém, não produzem nada por si sós.
Segundo BASSANEZI (2002);
[...] eles constituem um meio educacional auxiliar para apoiar a aprendizagem dos
alunos e permitem criar situações de aprendizagem estimulante. É outra maneira de
buscar e viabilizar a construção do conhecimento, de maneira mais autônoma e
independente, em um novo ambiente, onde os movimentos e as interações são
diferentes e obedecem a modelos. Além disso, abrem um novo leque de
possibilidades em função das inúmeras simulações que podem ser realizadas e dos
questionamentos que podem ser estabelecidos.
Desta maneira, o uso das ferramentas computacionais pode trazer grandes benefícios
ao ensino da matemática, mas para isso é necessário escolher programas e metodologia
adequados que tire proveito das características positivas do computador. Um bom exemplo
desse benefício, são as interfaces gráficas contidas em softwares matemáticos.
Na matemática, nem todos os problemas podem ser resolvidos através de fórmulas
prontas, por isso utilizam-se os métodos numéricos, os quais são técnicas matemáticas usadas
na solução de problemas matemáticos que não podem ser resolvidos ou que são difíceis de
resolver analiticamente. Assim, uma solução analítica é uma resposta exata na forma de uma
expressão matemática escrita em termos das variáveis associadas ao problema que está sendo
resolvido. Já uma solução numérica é um valor numérico aproximado para a solução, ou seja,
um número.
Embora soluções numéricas sejam uma aproximação, elas podem ser muito precisas.
Em muitos métodos numéricos, os cálculos são executados de maneira interativa até que a
precisão desejada seja obtida, ou seja, com o grau de precisão requerido. Como os métodos
numéricos de aparência fácil e de formulação teórica simples podem se revelar extremamente
difíceis quando executados manualmente, o computador revela a sua importância no auxílio
destes, por meio de softwares, pela capacidade de aceitar e executar automaticamente um
conjunto de instruções registradas internamente.
Porém, o uso do computador como ferramenta do cálculo numérico requer o
entendimento dos seus princípios de operação e de como eles interferem nos resultados
obtidos. Eles não resolvem todos os problemas, pois as máquinas produzem resultados que
determinadas instruções são fornecidas. Estas instruções podem provocar erros, e caso isso
7177
aconteça poderão ser quantificados, excluídos ou minimizados pelo usuário, provocando uma
maior análise e avaliação dos resultados esperados.
Segundo BARROS (1981, p. 4):
[…] Devido suas características, os computadores causaram um forte impacto nas
técnicas numéricas, provocando o abandono de algumas, reabilitação de outras e o
desenvolvimento de novas. O computador é um instrumento e, como tal, a qualidade
dos resultados que produz depende diretamente da capacidade e inteligência de
quem o usa [...]
Logo, os computadores, que cada vez mais auxiliam o cálculo numérico, são de suma
importância na resolução de problemas reais. Um exemplo disso é a previsão do tempo. O
problema a ser resolvido é grande, e os métodos numéricos utilizados são muito complicados,
pois a simulação numérica da previsão do tempo não pode ir além do período no qual a
previsão é necessária.
Os softwares matemáticos disponíveis têm potencialidades pedagógicas bastante
diversificadas, advém então a necessidade de escolha. O presente artigo utiliza-se software
Mathcad, pois não requer aprendizado demorado para o início da utilização e porque, dentre
outros, é o que apresenta características singulares: facilidade de elaboração de gráficos; as
equações são apresentadas como se escreve no papel, tem o objetivo de automatizar a
manipulação de cálculos matemáticos, expressões, fórmulas e equações, inclusive textos e
animações e facilidade de elaboração de rotinas computacionais.
Pela facilidade e excelentes ferramentas que este software disponibiliza será utilizado
para a elaboração de rotinas computacionais, a fim de resolver problemas envolvendo zeros
de funções polinomiais e transcendentes.
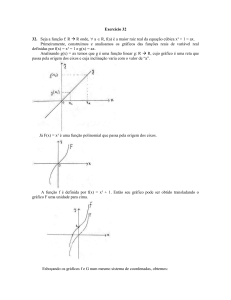
Resolução de Equações Algébricas e Transcendentes
Em muitos problemas práticos de aplicação matemática de Ciências e Engenharia, é
impossível determinar analiticamente a raiz de uma equação, ou seja, um número xr para o
qual:
f ( x r ) = 0 ⇒ x r é raiz de f(x)
Como a solução numérica de uma equação f(x) = 0 é um valor de x que satisfaz à
equação de forma aproximada, significa que quando o x é substituído na equação, o valor de
f(x) é próximo de zero, mas não exatamente zero.
7178
Considerando os problemas a seguir:
1) O preço à vista de um carro é de R$ 36.400,00, mas pode ser vendido à prazo em 48
prestações mensais de R$ 1297,95. Nessas condições, qual a taxa de juros mensal que estaria
sendo cobrada?
 (1 + i ) n − 1 
Da matemática financeira tem-se: PV = PMT .
n 
 i.(1 + i ) 
Logo:f(i) = 0 f (i) =
36400
.i.(1 + i) 48 − (1 + i) 48 + 1
1297,95
(1)
Pode-se observar que a função (1) acima descreve uma situação real, onde necessita
determinar a taxa (i), que dentre as várias, é uma delas a qual seja realmente a taxa utilizada
na operação, pois se sabe que como se trata de uma taxa que será cobrada ela não será zero
nem negativa, logo é necessário observar o intervalo positivo que contenha a raiz da referida
função.
Observando a função acima, pode-se concluir que tem-se uma equação algébrica (ou
Polinomial), pois, a variável aparece submetida a operações algébricas, repetidas um número
finito de vezes.
Desta forma, se x é esta variável, tem-se uma equação da forma:
Pn ( x ) = a n x n + a n −1x n −1 + an − 2 x n − 2 + ... + a 2 x 2 + a1x + a 0
onde: n ∈ Ν e a i ∈ R
2) A
área
As
da
parte
sombreada,
com
em
radianos,
é
dada
por:
7179
Então, pode-se escrever que
e,
(2) Se A = 3,6m²
e r = 3m, para determinar o ângulo θ, a equação deve ser resolvida para θ. Desta forma, temse:
Na equação (2), observa-se que a variável aparece submetida a operações não
algébricas em pelo menos um termo da equação, a qual é trigonométrica. Nestas equações, em
que pelo menos um termo, aparecem funções como: exponenciais, logarítmicas,
trigonométricas, etc., são denominadas equações transcendentes.
Embora esses métodos não determinem as soluções exatas, as raízes podem ser
calculadas com a exatidão que o problema requer desde que certas condições da função sejam
satisfeitas.
Observa-se que as funções (1) e (2) produzidas acima não possibilitam o procedimento
de obtenção de uma solução de forma analítica, e sim é necessário o processo de solução
numérica, que começa com a determinação de uma solução aproximada e é seguido de um
procedimento numérico no qual se determina uma solução mais precisa. Essa solução
numérica inicial pode ser estimada com o traçado de um gráfico, via tabela ou procedimento
analítico. Para tanto, à priori, é necessário considerar o teorema que segue.
Teorema de Bolzano e o Refinamento de Soluções
Para que uma função contínua y =
f(x) tenha no mínimo uma raiz no intervalo
[a, b], é suficiente, que ele tenha valores de
sinais opostos nos limites deste intervalo,
ou seja, f(x) assume valores de sinais
opostos nos pontos extremos do intervalo
fechado [a,b].
7175
•
Se f (a).f (b) < 0 , então o intervalo conterá no mínimo uma raiz (ou um n° ímpar de
raízes).
•
Se f (a ).f (b ) > 0 , então, a f(x) não tem nenhuma raiz real no intervalo ( ou o n° de
raízes será par).
•
A raiz x será definida e única se a derivada f`(x) for contínua e conservar o sinal
dentro do intervalo [a, b].
y = f(x)
f(a).f(b) < 0
xr∈ [a, b] ⇒ f(xr) = 0
Para o refinamento de uma solução, tem-se que Isolar a raiz, ou seja, achar um
intervalo [a,b], o menor possível, que contenha uma e somente uma raiz da equação f(x) = 0 e
em seguida melhorar o valor da raiz aproximada por meio de métodos iterativos.
Interpretação Geométrica dos Métodos e Procedimentos para Elaboração de Algoritmos
para Elaboração de Algoritmos para Refinar Raízes de Função
Refinar a raiz de uma função é melhorar o valor da raiz aproximada, isto é, refiná-la até o
grau de exatidão requerido, através de métodos iterativos, que são as sequências de instruções
que são executadas passo a passo, algumas repetidas em ciclos (iterações).
Os métodos Iterativos para se obter Zeros de Funções Algébricas e Transcendentes, são
métodos numéricos para determinação de raízes. Serão considerados a seguir os métodos da
Bisseção, Newton-Raphson e Iteração Linear.
Método da Bisseção (ou Dicotomia) – Método de quebra:
Dados f(x) uma função contínua no intervalo [a,b].
y
f(x)
x3 = xr
a
X0
X2
X1
b
x
7176
como : f (a ).f (b ) < 0
a+b
x0 =
2
f ( x 0 ).f (b) < 0
x1 =
x0 + b
2
f ( x 0 ).f ( x1 ) < 0
x2 =
x 0 + x1
2
f ( x 0 ).f ( x 2 ) < 0
x3 =
x0 + x2
= xr , com ε dado.
2
Critério de Parada:
Existem diferentes critérios de parada para assumir um resultado do zero de uma
função, basicamente são medidas distâncias sobre o eixo x, sobre o eixo y, determinado
número de iterações ou o erro relativo. Considerou-se para todos os métodos a serem
utilizados na resolução do problema de zeros de função o critério da medida da distância em
y, ou seja, |f(xn)| < ε.
Algoritmo do Método da Bisseção:
Dada função f(x):
Se
faça
(
recebe
Enquanto
)
> erro faça:
se
(
Senão
...
(
passa a ser )
Fim se;
Fim enquanto;
Programa Completo
Considerando o problema 2, com precisão de 10-4.
f( x) := 3.6 − 4.5⋅ ( x − sin ( x) )
passa a ser )
7177
4
2
f( x)
0
0.5
1
1.5
2
2
x
Por meio do software é possível visualizar o intervalo ao qual se encontra o zero da
função (a = 1,5 e b = 2). Esses dados, juntamente com a precisão pré-estabelecida e a função,
são considerados dados de entrada para os programas desenvolvidos a seguir. Por meio do
contador i e mat com seus índices de linha e coluna, é possível incrementar a variável linha,
possibilitando mostrar as iterações sob a forma de matriz.
7178
As variáveis que estão entre aspas, fornecem o cabeçalho da tabela, e as demais
mostram os resultados de cada iteração.
7179
Métodos de Ponto Fixo
São métodos que começam suas iterações de uma aproximação inicial x0, como
Newton-Raphson e Iteração Linear.
Método de Newton-Raphson (ou Método das Tangentes):
Graficamente, tem-se:
O método de Newton é equivalente a substituir um pequeno arco da curva y = f(x) por
uma reta tangente, traçada a partir de um dos pontos (a ou b) da curvatura.
Neste caso, é traçado a partir de Bo[xo, f(xo)], uma reta tangente a curva y = f(x), que
intercepta o eixo x no ponto x1. Do ponto B1 traçamos outra reta tangente a curva e o processo
se repete até que se encontre xr = xn, com tolerância requerida.
Geometricamente, pode-se mostrar que:
tg (α ) = f ' ( x0 ) =
f ( x0 )
x0 − x1
tg (β ) = f ' ( x1 ) =
f ( x1 ) , onde:
x1 − x2
Por indução:
, daí tem-se:
x 0 − x1 =
f ( x0 )
f ' ( x0 )
=> x1 = x0 − f ( x0 )
f ' ( x0 )
x 2 = x1 −
∴ x n +1 = x n −
f ( xn ) ,
f ' ( xn )
f ( x1 )
f ' ( x1 )
para n = 0,1,..
7180
Observe que ao partir do ponto A, o ponto x11 ∉ [a, b], então o método não
convergiria por A.
Logo, o método garante convergência desde que:
1. f’(x) e f’’(x) sejam não nulas e preservem o sinal em [a, b];
2. xo seja tal que f(x).f’’(x) > 0
Dados f(x) uma função contínua no intervalo [a,b].
Programa Básico
f( x) := 3.6 − 4.5⋅ ( x − sin ( x) )
f´( x) :=
f''( x) :=
d
f( x) → ( −4.5) + 4.5⋅ cos ( x) → ( −4.5) + 4.5⋅ cos ( x)
dx
d
2
2
f( x) → ( −4.5) ⋅ sin ( x)
dx
New( a , b , erro) :=
if f( a) ⋅ f( b) < 0
xo ← a if f( a) ⋅ f''( a) > 0
xo ← b otherwise
while f( xo) > erro
xn ← xo −
f( xo)
f´( xo)
xo ← xn
xn
New( 1.5, 2 , 0.0001) = 1.778506
Método da Iteração Linear:
Busca-se a intersecção da reta x com a curva g(x), e assim o método transforma o
problema de se encontrar uma raiz da equação f(x) = 0 na busca do ponto em que x = g(x).
7181
Y2=
g(x)
Sendo x0 a primeira aproximação da raiz xr, calcula-se g(x0). Faz-se então, x1 = g(x0), x2 =
g(x1), x3 = g(x2) e assim gera-se uma sequência de aproximação para a raiz pelo algoritmo:
x n = g( x n−1 ) para n = 0, 1, 2, ...
Programa Básico
f( x) := 3.6 − 4.5⋅ ( x − sin ( x) )
g( x) := 0.8 + sin ( x)
g´( x) :=
d
g( x) → cos ( x)
dx
MIL( a , b , erro) :=
if f( a) ⋅ f( b ) < 0
xn ← a if
g´( a) < g´( b )
xn ← b otherwise
while f( xn) > erro
x ← g ( xn)
xn ← x
xn
7182
MIL( 1.5, 2 , 0.0001) = 1.7785
Considerações Finais
Optou-se, para os estudos dos métodos do cálculo numérico, por uma função
transcendente e como critério de parada, a medida da distância em função do eixo das
ordenadas, ou seja, |f(xn)| < erro.
Para validar os programas desenvolvidos no Mathcad, o mesmo problema foi
resolvido manualmente com auxílio de calculadora científica para perceber o processo de
cálculo e posterior utilização da Planilha Excel. Desta forma, tornou-se possível o
desenvolvimento dos programas e avaliação da matriz de resultados dos métodos estudados
para a solução de zeros de funções polinomiais e transcendentes.
Ao término do desenvolvimento desse trabalho, constata-se que a utilização dos
programas na solução de problemas que envolvem zeros de funções torna possível, por meio
de alterações com relação aos dados de entrada: função, gráfico, intervalo e precisão e
também comparações quanto ao número de iterações, convergência, uso de derivadas, entre
outros, estudar desde modificações na visualização gráfica do problema bem como nos
possíveis resultados como a precisão desejada pertinentes aos cálculos. Seguem então
algumas conclusões: Comparando-se o resultado obtido pelos métodos da Bisseção, Iteração
Linear e de Newton-Rapshon observa-se que: No método da Bisseção a convergência é
garantida, porém, lenta; a aproximação não sai do intervalo inicial, esse intervalo é cada vez
dividido por dois; não exige o conhecimento de derivadas. O método de Newton requer o
conhecimento da forma analítica da derivada da função, mas sua convergência é
extraordinária. Já com relação ao método de Iteração Linear a maior dificuldade neste método
é encontrar uma função de iteração que satisfaça à condição de convergência; A velocidade de
convergência dependerá de |g'(x)|, quanto menor este valor maior será a convergência.
Assim, utilizando-se dos programas dos métodos numéricos desenvolvidos, pode-se
encontrar de maneira fácil as soluções de diferentes funções modificando apenas seus dados
de entrada, já na planilha Excel teriam que ser refeitos todos os cálculos.
7183
Considerando as conclusões citadas acima dos diferentes métodos numéricos para
encontrar zeros de funções, pode-se, por meio dos programas elaborados no Mathcad produzir
os mesmos resultados independente do uso de derivadas ou não, pois são calculadas
automaticamente pelo software.
REFERÊNCIAS
BARROS, Ivan de Queiroz. Introdução ao Cálculo Numérico. São Paulo: Editora Edgard
Blucher, 1972.
BASSANEZI, Rodney Carlos. Ensino Aprendizagem com Modelagem Matemática. São
Paulo: Contexto, 2002.