Raízes Complexas da Unidade

Raízes Complexas da Unidade
Conceito principal
A raiz da unidade, também conhecida como número de Moivré, é um número complexo z que
satisfaz
, para um inteiro positivo n.
Resolvendo para
a raiz da unidade
Note que o Maple usa a letra maiúscula I, ao invés da minúscula i, para apresentar a unidade
imaginária:
.
A representação
é um polinômio com coeficientes complexos e um grau de n, ele possui
raízes reais e complexas de acordo com o Teorema Fundamental da Álgebra.
Para resolver toda a
raiz da unidade, usamos o teorema de Moivré:
, onde x é um número complexo e n é um inteiro
(neste caso, em particular, x será qualquer número real e n qualquer número inteiro positivo).
Primeiro, converta o número complexo z a sua forma polar:
, onde
é
o modulo de z e é o ângulo entre o eixo positivo real (Re) e o segmento da reta que liga o ponto z
a origem do plano. Como
, é verdadeira para
, assim a equação anterior torna-se
simplesmente
.
Além disso, a conversão do número real
para qualquer número inteiro k.
, obtemos
Agora,
Moivré, esta equação torna-se
e assim usando o Teorema de
. Dessa
forma, pela equação veremos que,
Portanto, o
, ou equivalente a,
.
raíz da unidade pode ser expressa por esta fórmula
, para
Usando a fórmula de Euler:
.
, podemos escrever essa formula para
raíz da unidade na sua forma mais comum:
, para
a
.
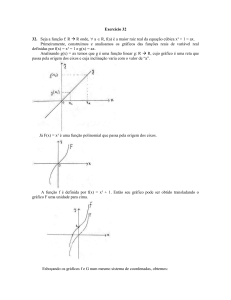
Quando o
raiz da unidade é traçada sobre o plano complexo (com a parte real [Re] no eixo
horizontal e a parte imaginária [Im] no eixo vertical), podemos ver que todas elas se encontram dentro
do círculo unitário e formam os vértices de um polígono regular de n lados.
>
Grau do polígono, n
0
5
10 15 20
Mostrar Polígo...
Links
updates/Maple17/MathApps