Exercício 32

Exercício 32
32. Seja a função f: R  R onde,  a  R, f(a) é a maior raiz real da equação cúbica x³ + 1 = ax.
Primeiramente, construímos e analisamos os gráficos das funções reais de variável real
definidas por f(x) = x³ = 1 e g(x) = ax.
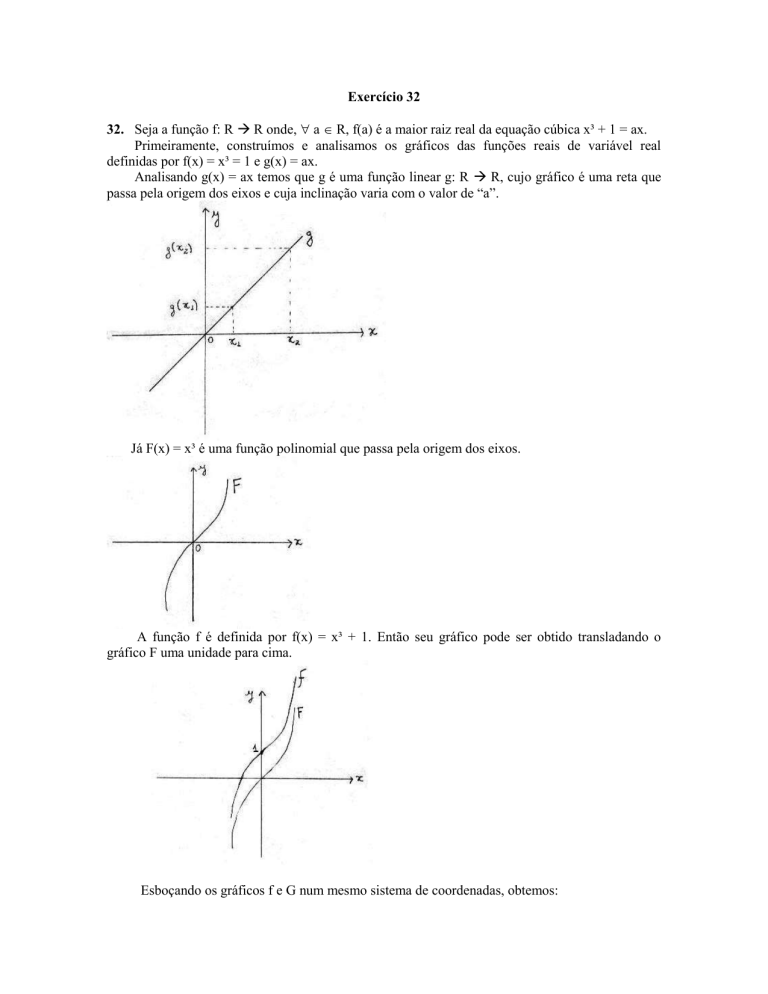
Analisando g(x) = ax temos que g é uma função linear g: R  R, cujo gráfico é uma reta que
passa pela origem dos eixos e cuja inclinação varia com o valor de “a”.
Já F(x) = x³ é uma função polinomial que passa pela origem dos eixos.
A função f é definida por f(x) = x³ + 1. Então seu gráfico pode ser obtido transladando o
gráfico F uma unidade para cima.
Esboçando os gráficos f e G num mesmo sistema de coordenadas, obtemos:
Obs.: Dependendo da inclinação de g haverá mais de um ponto de intersecção, mas como f(a)
é a maior raiz, consideremos apenas uma delas, a maior.
Analisando os gráficos verificamos que eles se interceptam em pelo menos um ponto, cuja
abscissa é a raiz da equação f(x) = g (x), definindo a função para a regra x³ + 1 = ax.
Desta forma, sempre haverá intersecção dos gráficos (pelo menos um ponto), sendo possível
indicar a maior raiz real da equação x³ + 1 – ax = 0.
Juntando os fatos:
1) Para todo “a” pertencente aos reais, existe f(a) porque, no mínimo em um ponto, as curvas
irão se interceptar.
2) Para todo “a” pertencente aos reais, existe e é única f(a), pois quando temos mais de um
ponto de intersecção tomamos apenas o que representa a maior raiz real.
Daí estabelecemos uma função por 1 e 2.