Lógica e teoria de conjuntos

matA10 – lógica e teoria de conjuntos
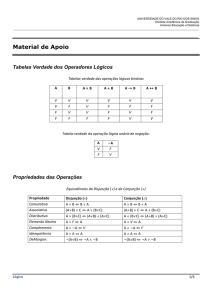
Proposições



Uma proposição é toda a expressão p suscetível de ser verdadeira ou falsa.
Uma proposição verdadeira tem o valor lógico de V ou 1 (verdade).
Uma proposição falsa tem o valor lógico de F ou 0 (falsidade).
Operações com proposições
Negação
Conjunção
p
~ p
p
q
pq
p
q
p q
V
F
F
V
V
V
F
F
V
F
V
F
V
F
F
F
V
V
F
F
V
F
V
F
V
V
V
F
Implicação
p
V
V
F
F
Disjunção
Equivalência
q
pq
V
F
V
F
V
F
V
V
p
V
V
F
F
Disjunção exclusiva
q
pq
p
q
p q
V
F
V
F
V
F
F
V
V
V
F
F
V
F
V
F
F
V
V
F
Propriedades das operações lógicas
Princípio da não contradição
Princípio do terceiro excluído
p ~ pF
p ~ pV
Comutatividade
pq  q p
Associatividade
pq  q p
Elemento neutro
pV  p
pF p
 p  q  r  p  q  r 
 p  q  r  p  q  r 
Elemento absorvente
pF F
pV  V
Distributividade
Leis de De Morgan
p  q  r    p  q   p  r 
~  p  q   ~ p ~ q
~  p  q  ~ p ~ q
p  q  r    p  q   p  r 
Implicação e disjunção
Negação da implicação
 p  q  ~ p  q
~  p  q   p ~ q
Implicação contrarrecíproca
Transitividade da implicação
 p  q    ~ q ~ p 
 p  q  q  r    p  r 
Dupla implicação
Dupla negação
 p  q  q  p   p  q
~ ~ p  p
Operação lógica e expressões
Operação
Conjunção   
Expressão
não
não é verdade que …
…e…
Disjunção   
… ou …
Negação  ~ 
www.matematicaonline.pt
[email protected]
Operação
Expressão
Implicação   
se … então …
Equivalência   
… se e somente se …
… se e só se …
1/2
matA10 – lógica e teoria de conjuntos
Expressão proposicional ou condição
Uma expressão proposicional ou condição é uma expressão p  x  envolvendo a variável x, tal que, substituindo a variável
por um objeto a, obtém-se uma proposição p  a  .
Quantificadores
Quantificador universal: 
Se p  x  é uma condição universal em U, a expressão x  U , p  x  é uma proposição verdadeira.
Quantificador existencial: 
Se p  x  é uma condição possível em U, a expressão x  U , p  x  é uma proposição verdadeira.
Condições
Representação
x U , p  x   x,  x U  p  x  
Impossíveis
Condições
Não universais
x  U : p  x   x : x  U  p  x 
Possíveis
Universais
Propriedades
Negação de uma condição
Se p  x  é uma condição qualquer, u  x  é uma condição
 A negação de uma condição impossível é uma condição
universal e i  x  é uma condição impossível, verifica-se:
universal.
p  x  u  x  u  x
p  x  u  x  p  x
 A negação de uma condição universal é uma condição
impossível.
p  x  i  x  p  x
p  x  i  x  i  x
 ~ x  U , p  x   x U : ~ p  x 

Segundas leis de De Morgan
~ x, p  x   x : ~ p  x 
~ x  U : p  x   x  U , ~ p  x 
Negação de uma implicação
~  x, p  x   q  x    x : p  x   ~ q  x 
~ x : p  x   x, ~ p  x 
Dupla implicação
x,  p  x   q  x     q  x   p  x    x,  p  x   q  x  
Contrarrecíproco
x,  p  x   q  x    x,  ~ q  x  ~ p  x  
Contraexemplo
Para provar que x  U , p  x  é uma proposição falsa, basta apresentar um contraexemplo, isto é, a  U , tal que p  a  é
falsa.
Conjuntos e condições
Condições definidas em U
a  x
Relações entre conjuntos-solução em U
A
b  x
B
~ a  x
negação
A
complementar
a  x  b  x
conjunção
A B
interseção
a  x  b  x
disjunção
A B
reunião (ou união)
a  x  b  x
implicação
A B
inclusão
a  x  b  x
equivalência
A B
igualdade

A  B   x : x  A  x  B

A  B   x : x  A  x  B

A \ B   x, x  A  x  B
www.matematicaonline.pt
[email protected]

A  B  x,  x  A  x  B 
 A BB  A A B
 Se B  A , então A \ B  B é o complementar de B em A
2/2