Lógica Proposicional

Lógica Proposicional
UESC
Disciplina: Fundamentos Matemáticos para Computação
Professor: Rogério Vargas
Alunos:
Álvaro Maciel, Caíque Martins, Diógenes Victor,
Giovanne Almeida, Leandro Oliveira.
Conceito
Lógica proposicional é um sistema no qual as fórmulas representam proposições
que podem ser formadas pela combinação de proposições atômicas usando
conectivos lógicos e um sistema de regras de inferência.
Conectivos lógicos
Conectivo
Significado
¬
não
^
e
v
ou
->
se... então
<->
se e somente se
∀
para todo
∃
existe
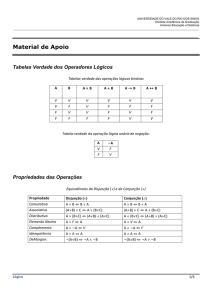
Tabela-Verdade
Tabela-verdade é um tipo de tabela matemática usada em Lógica para determinar
se uma fórmula é válida ou se um sequente é correto.
As principais Operações do Cálculo Proposicional:
•
•
•
•
•
Negação
Conjunção (E)
Disjunção (OU)
Condicional (Se... Então)
Bi-condicional (Se e somente se)
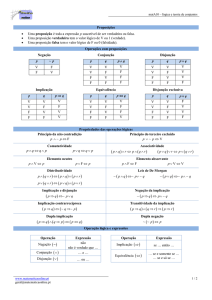
Regras de inferência
• Regras de negação: O operardor 'não é caso que' prefixa uma sentença para
formar uma nova sentença a qual é chamada negação da primeira. Assim, a
sentença 'Não é o caso que ele é fumante' é a negação da senteça 'Ele é
fumante'.
• Regras do condicional: Os enunciados formados por 'se... então' chamam-se
condicionais. O enunciado subsequente a 'se' é chamado antecedente; o
enunciado restante, consequente.
• Regras do bi-condicional: Os enunciados formados por 'se e somente se'
chamam-se bi-condicionais. Um bi-condicional pode ser considerado como uma
conjunção de dois condicionais.
Regras de inferência
• Regras de conjunções: A conjunção entre duas fórmulas só é verdadeira
quando ambas são verdadeiras.
• Regras de disjunção: A disjunção entre duas fórmulas só é verdadeira quando
ao menos uma delas é verdadeira.
• Regras para universal: A quantificação universal é válida para mostrar que para
todo e qualquer elemento de um determinado conjunto, as sentenças (afirmações
ou conjecturas) serão verdadeiras. Ou seja, para todo elemento escolhido no
conjunto a afirmação será verdadeira.
• Regras para existencial: Análogo ao quantificador universal, o existencial é
válido para mostrar que somente para alguns elementos de um determinado
conjunto, algumas sentenças serão verdadeiras. Ou seja, existe ao menos um
elemento no conjunto que torne a afirmação verdadeira.