rial e, como vimos, descreve a implic

Resumos - Lógica - Prof. Ricardo P. Tassinari - Departamento de Filosofia - Unesp/Marília – 2012
A IMPLICAÇÃO MATERIAL
E SEUS
PARADOXOS
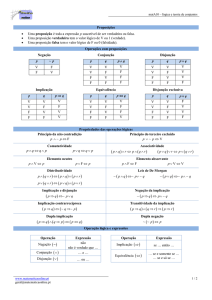
A implicação descrita apenas pelo conectivo condicional é chamada de implicação material e, como vimos, descreve a implicação apenas em termos dos valores-verdade de seus
constituintes.
Nesse sentido, temos que, se considerarmos a sentença
A Lua é de queijo → 1=1
temos que essa sentença é verdadeira, pois, neste caso, tanto seu antecedente é falso,
quanto seu conseqüente é verdadeiro.
A condicional é a forma com que Frege introduz a implicação em sua Conceitografia (cf.,
por exemplo, Frege, 2009, p.74).
Podemos notar, como faz Frege (idem, p. 75), que "A linguagem corrente não permite
que se traduza esse sinal em todos os casos por 'se[… então _]'." Sem dúvida, neste caso,
parece-nos estranha a sentença:
Se a Lua é de queijo, então 1=1.
As sentenças que contém implicações materiais e que parecem contradizer a noção intuitiva de implicação expressa por "se … então _" são chamadas de Paradoxos da Implicação
Material.
Podemos nos perguntar: para que usar uma forma de implicação que nos causa estranhamento ao traduzi-la em termos de "se … então _"?
Como vimos, porque, ela simplifica o tratamento da implicação do ponto de vista de uma
conceitografia, bem como de sua interpretação, na medida em que:
(1) o valor-verdade da fórmula composta A→B é determinado apenas pelos valores-verdade de A e de B, sem que se precise considerar qualquer outro dado; e
(2) evita as dificuldades naturais em se tentar caracterizar o que seria a noção mais
complexa de implicação.
Existe um ramo da Lógica, chamada de Lógica da Relevância que estuda sistemas formais com uma noção de implicação que evitam os paradoxos da implicação material. Entretanto esses sistemas formais inserem maiores complicações do que a conceitografia que
está sendo aqui exposta, e, em geral, por causa disso, usamos a lógica aqui apresentada para
o próprio estudo da Lógica da Relevância.
Por fim, notemos que mesmo que estranhemos a definição de implicação em termos da
implicação material, esse estramento deixa de existir se entendermos que essa implicação,
da forma A→B, é definida por: não ocorre A ou ocorre B. Assim, a sentença
“A Lua é de queijo → 1=1”
expressa:
A Lua não é de queijo ou 1=1.
E essa sentença é verdadeira, pois é a disjunção de duas sentenças verdadeira, pois
tanto a Lua não é de queijo quanto 1=1.