AULA 5 Atividade 13 – Simetria a) Faça uma reta vertical dividindo a

AULA 5
Atividade 13 – Simetria
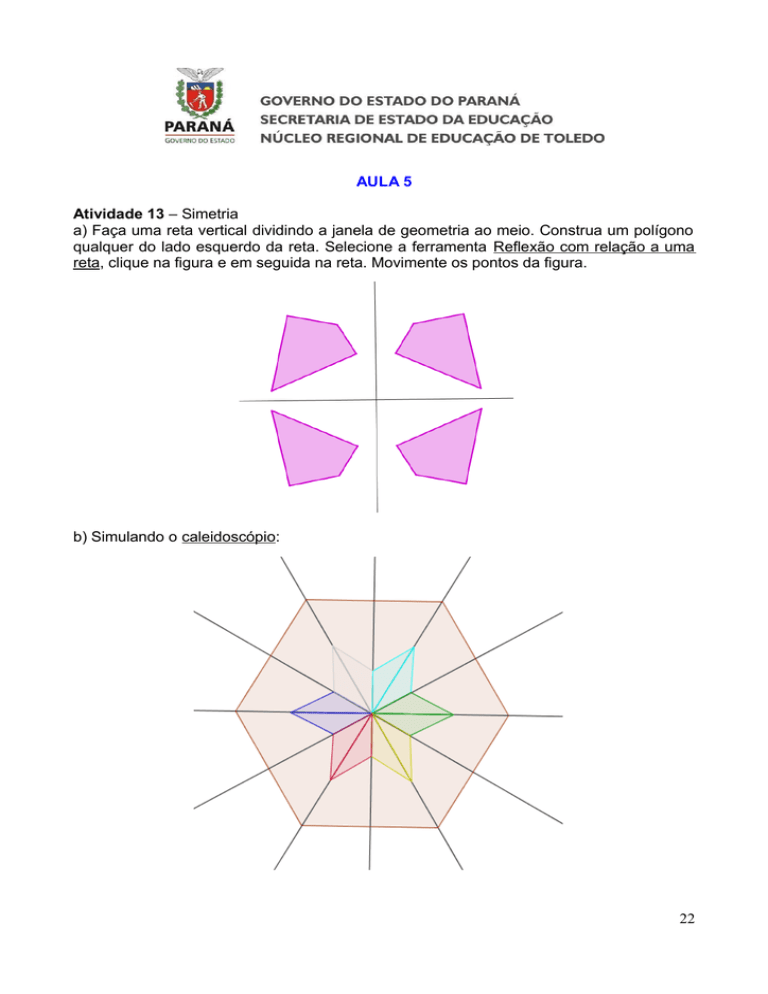
a) Faça uma reta vertical dividindo a janela de geometria ao meio. Construa um polígono
qualquer do lado esquerdo da reta. Selecione a ferramenta Reflexão com relação a uma
reta, clique na figura e em seguida na reta. Movimente os pontos da figura.
b) Simulando o caleidoscópio:
22
Atividade 14 – Figuras Geométricas Planas: Triângulos
a) Construa um triângulo qualquer. Observe as medidas dos lados do triângulos, na
janela algébrica. Marque os ângulos internos do triângulo e observe suas medidas
na janela algébrica. Movimente um dos vértices e descreva o que você observou
quanto à medida dos ângulos internos.
b) Construa um triângulo equilátero utilizando a ferramenta Polígono. Observe as
medidas dos lados do triângulo, na janela algébrica. Movimente um dos vértices e
confira sua construção. Marque os ângulos internos do triângulo e observe suas
medidas na janela algébrica. Movimente, novamente, um dos vértices e descreva o
que você observou quanto à medida dos ângulos internos. Determine sua altura,
uma de suas bissetrizes, a medida de sua altura, seu perímetro, sua área, e a
mediatriz de um de seus lados.
Construindo um triângulo equilátero pela definição:
- clicar na ferramenta Segmento definido por Dois Pontos, construir um segmento de
reta AB de medida qualquer;
- com a ferramenta Círculo dados Centro e Um de seus Pontos, clicar sobre o vértice A
e, posteriormente, em B para criar uma circunferência de centro A e raio AB;
- com a ferramenta Mediatriz, clicar sobre o segmento AB;
- marcar o ponto C comum a mediatriz e a circunferência com a ferramenta Interseção de
Dois Objetos;
- unir os vértices A e C com segmento de reta, bem como, os vértices B e C,
determinando um novo triângulo ABC, neste caso, equilátero;
- selecionar a circunferência, clicar com o botão inverso do mouse para selecionar Exibir
Objeto;
- analogamente, selecionar a reta mediatriz, clicar com o botão inverso do mouse para
selecionar Exibir Objeto;
- com a ferramenta Polígono, clicar sobre os vértices do triângulo para preencher o
polígono triangular;
23
Questões:
1) Somando-se as medidas dos três ângulos do triângulo equilátero construído, o que
você pode concluir?35
2) Há alguma particularidade nas medidas destes ângulos? 36
3) Clique sobre o ponto B e arraste-o para os lados. O que acontece com as medidas
dos ângulos? Como fica a soma destas medidas? O triângulo continua tendo alguma
particularidade?
c) Construa um triângulo isósceles. Observe as medidas dos lados do triângulo, na
janela algébrica. Movimente um dos vértices e confira sua construção. Marque os
ângulos internos do triângulo e observe suas medidas na janela algébrica.
Movimente, novamente, um dos vértices e descreva o que você observou quanto à
medida dos ângulos da base.
Construindo um triângulo isósceles por conceito:
- clicar na ferramenta Segmento definido por Dois Pontos, construir um segmento de
reta AB de medida qualquer;
- com a ferramenta Mediatriz, clicar sobre o segmento AB;
- com o botão Novo Ponto selecionado, criar um ponto C qualquer sobre a reta mediatriz;
- construir os segmentos AC e BC com a ferramenta Segmento definido por Dois
Pontos;
- com o triângulo ABC definido, pode-se “esconder” a reta mediatriz que dá origem a esta
figura, uma vez que ela não será mais necessária durante nosso estudo; para isso, clicar
com o botão inverso do mouse sobre a mediatriz e selecionar Exibir Objeto;
- para marcar as medidas dos ângulos do triângulo ABC, selecionar a ferramenta Ângulo
e clicar, sequencialmente, nos pontos CBA, ACB e BAC (os ângulos são dados
selecionando-se os pontos da direita para esquerda, caso contrário, ele exibe o ângulo
externo àquele vértice).
35 Que a soma das medidas dos ângulos internos continua sendo 180º.
36 Que todos os ângulos internos são iguais a 60º, característica dos triângulos equiláteros.
24
Questões:
1) Somando-se as medidas dos três ângulos do triângulo isósceles construído, o que
você pode concluir?37
2) Há alguma particularidade nas medidas destes ângulos? 38
3) Clique sobre o ponto C e arraste-o para cima e para baixo. O que acontece com as
medidas dos ângulos? Como fica a soma destas medidas? O triângulo continua tendo
alguma particularidade?
d) Construa um triângulo retângulo. Marque os ângulos internos do triângulo e
observe suas medidas na janela algébrica. Movimente um dos vértices e confira
sua construção.
e) Salve seu arquivo como atividade10_nomecursista.ggb.
Atividade 15 – Quadriláteros
a) Construir um quadrilátero qualquer:
- com a ferramenta Novo Ponto, marcar quatro pontos quaisquer sobre a janela de
visualização;
- definir um Polígono ABCD, clicando sobre os pontos criados A, B, C, D e A (note que
será necessário clicar novamente sobre o primeiro ponto clicado a fim de “fechar” o
polígono);
- marcar os Ângulos deste polígono;
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
Questões:
1) As medidas dos lados deste quadrilátero são iguais? E as medidas dos ângulos?
b) Construir um paralelogramo:
- marcar um Segmento definido por Dois Pontos EF, a partir desta ferramenta;
- marcar um segundo Segmento definido por Dois Pontos EG, sendo E uma das
extremidades do segmento construído no passo anterior;
- traçar Reta Paralela selecionando esta ferramenta e clicando sobre o ponto G e o
segmento EF;
- analogamente, construir Reta Paralela clicando sobre o ponto F e o segmento EG;
- com a ferramente Interseção Entre Dois Objetos, selecionar as duas retas construídas
anteriormente para definir o ponto H;
- clicar com o botão inverso do mouse em cada uma das retas e desmarcar a opção Exibir
Objeto;
- definir um Polígono EFGH clicando sobre os pontos A, F, H, G e E;
- marcar os Ângulos deste polígono;
37 Que a soma das medidas dos ângulos internos continua sendo 180º.
38 Que dois dos ângulos internos são iguais, característica dos triângulos isósceles.
25
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
c) Construir um trapézio:
- marcar um Segmento definido por Dois Pontos IJ;
- marcar um segundo Segmento definido por Dois Pontos IK, sendo I uma das
extremidades do segmento construído no passo anterior;
- traçar Reta Paralela selecionando esta ferramenta e clicando sobre o ponto K e o
segmento IJ;
- criar um Ponto Novo L sobre esta reta paralela e que esteja no mesmo lado do ponto J,
em relação ao segmento IK;
- clicar com o botão inverso do mouse na reta paralela e desmarcar a opção Exibir Objeto;
- definir um Polígono IJKL clicando sobre os pontos I, J, L, K e I;
- marcar os Ângulos deste polígono;
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
d) Construir um paralelogramo com medidas dos lados iguais:
- marcar um Segmento definido por Dois Pontos MN, a partir desta ferramenta;
- construir uma Circunferência dados Centro e Um de seus Pontos, com centro em M e
raio MN;
- marcar um Ponto Novo O sobre esta circunferência;
- traçar o Segmento definido por Dois Pontos MO;
- clicar com o botão inverso do mouse sobre a circunferência e desmarcar a opção Exibir
Objeto;
- traçar Reta Paralela selecionando esta ferramenta e clicando sobre o ponto O e o
segmento MN;
- analogamente, construir Reta Paralela clicando sobre o ponto N e o segmento MO;
- com a ferramente Interseção Entre Dois Objetos, selecionar as duas retas construídas
anteriormente para definir o ponto P;
- clicar com o botão inverso do mouse em cada uma das retas e desmarcar a opção Exibir
Objeto;
- definir um Polígono MNOP clicando sobre os pontos M, N, P, O e M;
- marcar os Ângulos deste polígono;
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
e) Construir um paralelogramo com as quatro medidas de ângulos iguais (o que só ocorre
para todos os ângulos de medida 90º):
- marcar um Segmento definido por Dois Pontos QR, a partir desta ferramenta;
- traçar Reta Perpendicular, clicando sobre o ponto Q e o segmento QR;
- analogamente, traçar Reta Perpendicular clicando sobre o ponto R e o segmento QR;
- criar um Ponto Novo S sobre a reta perpendicular que passa pelo ponto Q;
- traçar Reta Paralela clicando sobre o ponto S e o segmento QR;
26
- clicar com o botão inverso do mouse sobre a circunferência e desmarcar a opção Exibir
Objeto;
- com a ferramente Interseção Entre Dois Objetos, definir o ponto T entre a reta
perpendicular que passa pelo ponto R e a reta paralela ao segmento QR;
- clicar com o botão inverso do mouse em cada uma das retas construídas e desmarcar a
opção Exibir Objeto;
- definir um Polígono QRST, clicando sobre os pontos Q, S, T, R e Q;
- marcar os Ângulos deste polígono;
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
f) Construir um paralelogramo com a medida dos quatro lados iguais e as quatro medidas
de ângulos iguais:
- marcar um Segmento definido por Dois Pontos UV, a partir desta ferramenta;
- traçar Reta Perpendicular, clicando sobre o ponto U e o segmento UV;
- analogamente, traçar Reta Perpendicular clicando sobre o ponto V e o segmento UV;
- construir uma Circunferência dados Centro e Um de seus Pontos, com centro em U e
raio UV;
- com a ferramente Interseção Entre Dois Objetos, definir o ponto W entre a reta
perpendicular que passa pelo ponto U e a circunferência de centro U;
- construir uma Circunferência dados Centro e Um de seus Pontos, com centro em V e
raio UV;
- com a ferramente Interseção Entre Dois Objetos, definir o ponto Z entre a reta
perpendicular que passa pelo ponto V e a circunferência de centro V;
- clicar com o botão inverso do mouse sobre as circunferências e desmarcar a opção
Exibir Objeto;
- clicar com o botão inverso do mouse em cada uma das retas perpendiculares
construídas e desmarcar a opção Exibir Objeto;
- definir um Polígono UVWZ, clicando sobre os pontos U, V, Z, W e U;
- marcar os Ângulos deste polígono;
- marcar as medidas dos lados deste polígono com a ferramenta Distância, Comprimento
ou Perímetro;
27