baixe o arquivo em

Geometria analítica: descobrindo a reta
que tange duas circunferências e
entendendo a construção geométrica.
Sobre
Ontem estava pensando em algumas funções interessantes para implementar
em um editor de imagem vetorial e me veio em mente traçar guias tangenciando
circunferências simultaneamente. Fiz uma busca rápida e encontrei apenas a
construção geométrica (clique para abrir em nova aba) no blog “O baricentro da
mente”.
A construção
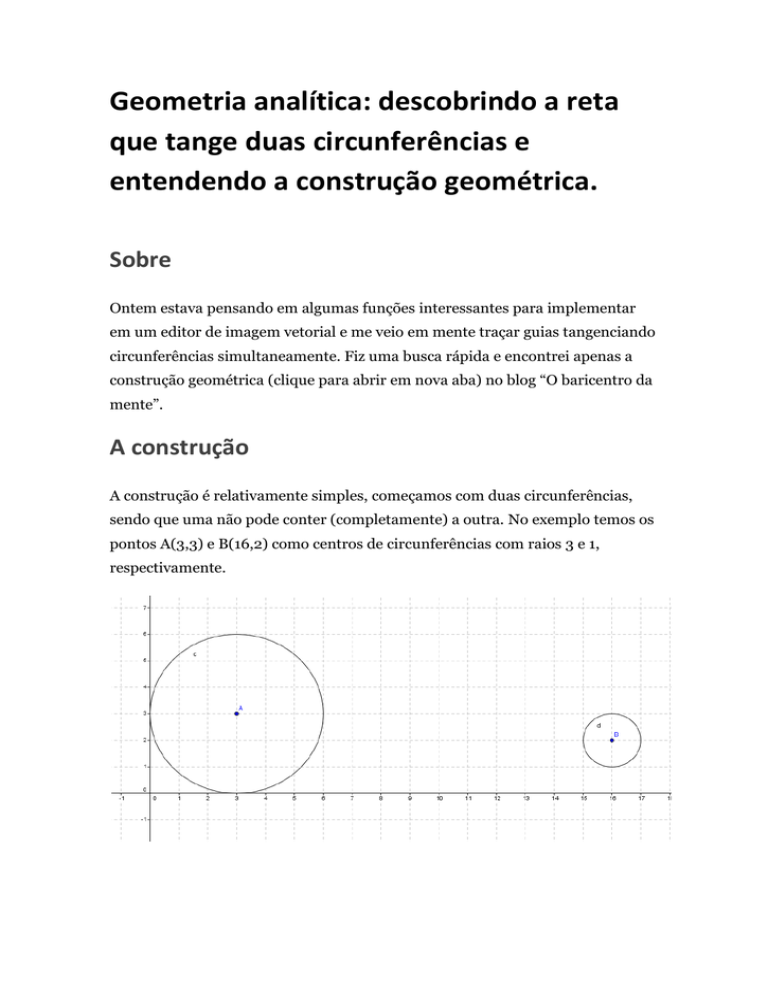
A construção é relativamente simples, começamos com duas circunferências,
sendo que uma não pode conter (completamente) a outra. No exemplo temos os
pontos A(3,3) e B(16,2) como centros de circunferências com raios 3 e 1,
respectivamente.
Outra circunferência é criada para auxiliar o desenho, sendo que ela possui o
mesmo centro que a maior e o raio resultante da subtração do raio maior e do
menor. No exemplo teremos uma circunferência com centro em A e raio 2.
Depois traçamos o ponto médio (C) entre os centros, no exemplo C(9,5 ; 2,5).
Depois basta construir uma circunferência com centro em C e diâmetro AB.
Usando o ponto A e os pontos de intercessão dos dois círculos auxiliares,
traçamos duas retas, até a intercessão com o círculo maior.
Traçando os segmentos BD e BE e depois prolongando retas paralelas até os
pontos em laranja (intercessões na circunferência maior) temos as duas retas
que tangenciam simultaneamente as duas circunferências.
A lógica da coisa
Toda construção geométrica não passa da representação de processos algébricos
na forma de desenho. Essa forma que apresentei visa simplificar a construção
“transformando” a circunferência menor em um ponto.
Para que uma reta tangencie uma circunferência em um ponto P é preciso que o
ângulo entre a reta e o segmento que parte do centro até P seja reto. Observe na
figura acima a reta que passa pelos pontos de tangência F e E, considerando a
formação do ângulo reto nesses pontos podemos afirmar que as semi-retas que
partem do centro das circunferências até o ponto de tangência são paralelas
entre si e perpendiculares à reta tangente.
A reta que passa pelos pontos B e D é paralela à reta tangente, sendo
perpendicular as retas vermelhas, mas com o diferencial de passar pelo centro
da circunferência menor. A subtração dos raios existe simplesmente para
deslocar a reta e permitir que ela passe pelo centro.
Agora precisamos resolver mais um problema: como determinar o ponto onde
passa a reta tangente no círculo criado pela subtração dos raios?
Uma propriedade interessante das circunferências é que unindo um ponto
qualquer do perímetro com o segmento do diâmetro o triângulo formado será
retângulo. Veja no exemplo acima.
Aqui está a grande sacada dessa construção: considerando o segmento AB o
diâmetro de uma circunferência de centro C temos que qualquer ponto de
intercessão no perímetro dessa circunferência formará um triângulo retângulo.
Olhando por outra ótica: a reta que contém o cateto DB é tangente à
circunferência de centro A e passa por B. Acompanhe abaixo:
Agora basta criar uma reta paralela a reta do cateto BD e movê-la na reta que
contém AD uma distância correspondente ao raio do círculo de centro em B.
A matemática da coisa
Dadas as circunferências c e d, com centros em A(1,7) e B(4,2) e raios 2 e 2 2,
respectivamente, encontre que tangencia simultaneamente as circunferências.
Podemos desenhar o círculo auxiliar com centro em B, que deve ter raio
2 2−
2=
2 e marcar o ponto médio M entre os centros:
1+4 7+2
,
→ 𝑀 2,5 ; 4,5
2
2
𝑀
Podemos agora definir o raio da circunferência de diâmetro AB e centro em M:
𝑟=
𝑥𝑎 − 𝑥𝑏
𝑟=
2
+ 𝑦𝑎 − 𝑦𝑏
2
2
34
2
As equações que representam a circunferência de centro em M e a
circunferência auxiliar de centro em B são:
𝑒: 𝑥 − 4
𝑓:
5
𝑥−
2
2
+ 𝑦−2
2
2
9
+ 𝑦−
2
2
= 2
=
34
4
Desenvolvendo as equações, temos:
𝑒: 𝑥² − 8𝑥 + 𝑦² − 4𝑦 = −18
𝑓: 𝑥² − 5𝑥 + 𝑦² − 9𝑦 = 18
Subtraindo as equações:
𝑡: − 3𝑥 + 5𝑦 = 0
A reta “t” resultante está destacada de laranja na imagem abaixo e ela possui os
dois pontos de intercessão das circunferências “e” e “f”:
Isolando uma variável da reta e substituindo em “e” ou “f”, temos:
𝑦=
𝑥 2 − 8𝑥 +
3𝑥
5
3𝑥
5
2
−4
3𝑥
= −18
5
𝑥 ′ = 5 𝑒 𝑥 ′′ =
45
17
𝑦 ′ = 3 𝑒 𝑦 ′′ =
27
17
𝐷 5 ,3 𝑒 𝐶
45 27
,
17 17
Para descobrir as retas que tangem a circunferência auxiliar “e” basta encontrar
as retas que contém os segmentos AC e AD, exemplificarei apenas para AD.
A equação da reta “s” que contém AD – que está destacada de laranja é:
𝑠: 𝑥 + 𝑦 = 8
Agora é hora de “subir” a reta de forma que ela tangencie as duas
circunferências originais, vamos começar traçando o caminho por onde se dará
o deslocamento, a reta “v”, que contém o segmento BD:
𝑣: 𝑥 − 𝑦 = 2
O segmento que representa o deslocamento (representado pela fecha vermelha)
possui o mesmo comprimento que o raio da circunferência “c”, já que ele é a
parte do raio da circunferência “d” reduzida para formar a circunferência “e”,
ambas concêntricas.
Podemos imaginar o deslocamento como um vetor e decompor em um
deslocamento vertical e outro horizontal, logo:
𝑑𝑡 ² = 𝑑𝑣 ² + 𝑑ℎ ²
Tomando o deslocamento vertical como sendo x, e considerando a equação geral
da reta, temos:
𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0
Para cada aumento de A vezes na horizontal (x) há um aumento de B vezes na
vertical (y), logo:
𝑑ℎ = 𝑥
𝑑𝑣 =
𝐵𝑥
𝐴
E para descobrir x:
𝑑𝑡 ² = 𝑥² 1 +
𝐵²
𝐴²
Esses valores informam o deslocamento em vertical ou horizontal sobre um
caminho retilíneo, e é notável que um deslocamento vertical apenas soma (ao
subir) ou subtrai (ao descer) um valor 𝑑𝑣 no termo isolado (C). Já um
deslocamento horizontal soma (para a esquerda) ou subtrai (para a direita) um
valor 𝑑𝑥 ∗ 𝐴 no termo isolado (C).
Voltando ao exemplo temos que mover a reta “s” sobre a reta “v”, sendo suas
equações na forma geral:
𝑠: 𝑥 + 𝑦 − 8 = 0
𝑣: 𝑥 − 𝑦 − 2 = 0
Como o deslocamento ocorre sobre a reta “v” e possui o comprimento de 2,
temos:
2 ² = 𝑥² 1 +
(−1)²
(1)²
𝑥 = 1 ; 𝑑𝑣 = 1 ; 𝑑ℎ = 1
Considerando a reta “s” deslocada para a direita e para cima:
𝑠′: 𝑥 + 𝑦 − 8 – 𝑑𝑥 ∗ 𝐴 − 𝑑𝑣 = 0
𝑠′: 𝑥 + 𝑦 − 10 = 0
E ai a reta que tange as duas circunferências citadas!
Um caminho provavelmente mais simples seria após descobrir a reta que tange
a circunferência auxiliar e o centro da menor circunferência manter o
coeficiente angular (A), substituir na equação de um dos círculos originais,
reduzir a equação para duas raízes e eliminar a possibilidade que não tange.
Em anexo está um modelo interativo no Geogebra com essa construção.