td matematica_waldeglacepopular!

Fundação Universidade Estadual do Ceará - FUNECE
Pró-Reitoria de Políticas Estudantis – PRAE
Curso Pré-Vestibular UECEVest
Fone: 3101. 9658/ E-mail: [email protected]
Av. Paranjana, 1700 – Campus do Itaperi – 60740-903
Prof: Waldeglace
Aula do dia 25 de abril
Analise combinatória
1. O número de modos diferentes de escolher quatro
elementos (números) distintos
no
conjunto
{-6,-5,-4,-3,-2,-1,1,2,3,4,5,6} de tal forma que o produto
destes números seja positivo, é:
A) 324.
B) 255.
C) 225.
D) 216.
9. Para n e k inteiros positivos com n > k, defina
2.Dispõe-se de cinco cores distintas para confeccionar
bandeiras com três linhas horizontais de mesma
largura. O número de bandeiras diferentes que se
pode confeccionar, exigindo-se que listas vizinhas não
tenham a mesma cor, é igual a
A) 75.
B) 80.
C) 85.
D) 90.
Geometria Plana e Espacial
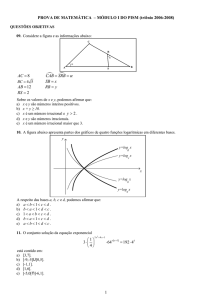
10. A figura construída em papelão plano, com área
2
igual a 33m é formada por um quadrado cujo lado
mede x metros e por quatro retângulos com lados
medindo 2 e x metros.
𝑛
𝑛!
= 𝑘! 𝑛−𝑘 !, onde n! = 1.2.3. ... . n. Se n e k
𝑘
satisfazem a relação
A) n = 4k + 1.
B) n = 4k + 2.
𝑛
𝑛
=3
, então tem-se
𝑘+1
𝑘
C) n = 4k + 3.
D) n = 4k + 2.
2
Logaritmo
3. Se f, g: são funções definidas por
2
x
f(x)=log7(x + 1) e g(x)= 7 . O valor de g(f(1)).g(f(0)) é:
A) 0.
B) 1.
C) 2.
D) 7.
4. Considerando log23 = k podemos afirmar,
corretamente, que a soma das raízes da equação
x
-x
2 – 12 + 27.2 = o é igual a
A) 2k.
B) 3k.
C) 2/k.
D) 3/k.
Trigonometria
5. Se p e q são, respectivamente, os valores máximos
e mínimos da função real de variável real definida por
1
2
f(x) = 2 - cos x, então o produto p.q é igual a
2
A) 2.
B) 3.
C) 2 .
D) 3.
6. O conjunto-imagem da função f: R→ R, definida por
2
f(x) = 2cos2x + cos x, é o intervalo
A) [-2, 1].
B) [-2, 3].
C) [-2, 2].
D) [-2, 0].
x
A caixa paralelepípedo, obtida dobrado os retângulos
nas linhas pontilhadas, limita no seu interior um
volume igual a
A) 18m³.
B) 21m³.
C) 24m³.
D) 27m³.
11. Uma metalúrgica recebeu uma encomenda para
fabricar, em grande quantidade, uma peça com o
formato de um prisma reto com base triangular, cujas
dimensões da base são 6 cm, 8 cm e 10 cm e cuja
altura é 10 cm. Tal peça deve ser vazada de tal
maneira que a perfuração na forma de um cilindro
circular reto seja tangente às suas faces laterais,
conforme mostra a figura.
7. Sejam a = logcos, b = logsen e c = log2 e
a + b + c = 0. Os logaritmos são decimais e
0° <  < 90°. Podemos afirmar, corretamente, que o
ângulo  está situado entre
A) 50° e 60°. B) 30° e 40°. C) 40° e 50°. D) 20° e 30°.
Binômio de Newton
8. O termo independente de x, no desenvolvimento de
2x +
A) 249.
1 12
2x
é igual a
B) 270.
C) 720.
D) 924.
O raio da perfuração da peça é igual a
A) 1 cm.
B) 2 cm.
C) 3 cm.
D) 4 cm.
12. O triângulo, cujos vértices são os pontos (0,0),
(0,2) e (1,1), ao girar em torno do eixo dos y gera uma
3
região no  cujo volume é
A)
2
u.v .
3
B) 4 u.v.
3
C)

u.v.
3
D)   1 u.v.
3
13. Uma empresa precisa comprar uma tampa para o
seu reservatório, que tem a forma de um tronco de
cone circular reto, conforme mostrado na figura.
Considere que a base do reservatório tenha raio
r = 2 3 m e que sua lateral faça um ângulo de 60°
com o solo.
Se a altura do reservatório é 12 m, a tampa a ser
comprada deverá cobrir uma área de
2
2
2
2
A) 12m .
B) 54m .
C) 108m . D) 300m .
14. O volume de um prisma regular reto hexagonal,
com 2m de altura, é 3𝑚3 . A medida da área lateral
deste prisma é
A) 3𝑚2 .
B) 2 3𝑚2 .
C) 3 3𝑚2 . D) 4 3𝑚2 .
Matemática básica
18. Uma fatura foi paga com acréscimo de 12% sobre
o seu valor nominal, porque o pagamento foi efetuado
após o vencimento. Se o valor pago foi R$ 1.209,60,
então o valor nominal da fatura estava entre
A) R$ 1.030,00 e R$ 1.045,00.
B) R$ 1.045,00 e R$ 1.060,00.
C) R$ 1.060,00 e R$ 1.075,00.
D) R$ 1.075,00 e R$ 1.090,00.
19. Dois digitadores (de computador) executaram o
mesmo serviço de digitação em tempos diferentes. O
mais experiente consegue completas o trabalho em
duas horas enquanto o outro completa o trabalho em
três horas. O objetivo é realizar o trabalho no menor
tempo possível, distribuindo parte do trabalho com
cada um dos digitadores, de forma que, ambos
concluam, juntos, suas tarefas, executando o trabalho
completo. Esse tempo mínimo será
A) 72 minutos.
C) 95 minutos.
B) 90 minutos.
D)150 minutos.
Progressões
20. A seqüência a1 , a2 , a3 , a4,... é constituída por
números reais e é definida por a1= 1/3 e, para n > 1,
an =
a 𝑛 −1
3
. Se S é a soma dos termos da sequência,
então log2S é igual a
-1
A) 3 .
B) 1.
Geometria Analítica
15. O comprimento da corda determinada pela reta
2
2
x + 7y – 50 = 0 na circunferência x + y – 100 = 0 é
A) 2 5 u.c. B) 5 2 u.c. C)2 10 u.c. D)10 2 u.c.
16. A menor distância entre os pontos do plano
2
cartesiano R , com coordenadas inteiras e que estão
sobre a reta y = 3x + 1 é
A) 1 u.c.
B) 2 u.c. C) 5 u.c.
D) 10 u.c.
17. Se as equações das circunferências M e P, no
sistema de coordenadas cartesianas Usual, são
2
2
respectivamente x + y – 6x – 10y + 18 = 0 e
2
2
x + y – 12x – 8y + 36 = 0, pode-se afirmar
corretamente que
A) M e P são concêntricas.
B) M e P são tangentes.
C) M e P possuem raios com medidas diferentes.
D) M e P possuem exatamente dois pontos na
interseção.
C) 0.
D) -1.
21.O valor do inteiro positivo n para o qual
1+3+5+⋯+(2𝑛 −1)
1
=
é
𝑛 2 (2+4+8+⋯+2𝑛 )
254
A) 7.
B) 8.
C) 9.
D) 10.
22. Se os números reais positivos m, n, e p formam,
nesta ordem, uma progressão geométrica, então a
soma log m + log n + log p é igual a
A) 2 log n. B) 3 log n. C) 4 log n. D) 5 log n.
Conjuntos
23. Dos 200 professores de uma universidade, 60
dedicam tempo integral a essa instituição e 115 são
doutores. Se entre os doutores apenas 33 dedicam
tempo integral, então o número de professores da
universidade que não dedicam tempo integral e não
são doutores é
A) 107.
B) 82.
C) 58.
D) 55.
24. Se X e Y são conjuntos tais que, X possui
exatamente vinte elementos e Y possui exatamente
sete elementos, então pode-se afirmar corretamente
que
A) a união do conjunto X com o conjunto Y tem no
mínimo sete elementos e no máximo vinte elementos.
B) a interseção do conjunto X com o conjunto Y tem
no máximo sete elementos.
C) se X  Y ≠  a diferença X – Y terá seis elementos.
D) se X  Y ≠  a diferença X – Y será o conjunto
vazio.
Função
25. No mundo empresarial é costumeira a realização
de análise da evolução patrimonial, do faturamento
anual, do volume comercializado e do lucro das
empresas,
dentre
outros
segmentos
de
acompanhamento e controle.
A Associação Brasileira do Meio Hoteleiro – ABMH
constatou que o faturamento anual das empresas
associadas quase dobrou no período 2006 a 2011,
passando de 8 bilhões de reais em 2006 para 15,8
bilhões em 2011.
Admitindo-se que a evolução observada ocorreu de
forma linear crescente no período analisado, é
possível afirmar corretamente que faturamento anual
no ano de 2009, em bilhões de reais, foi de
A) 11,12. B) 11,80.
C) 12,68.
D) 13,40.
26. A parábola que é o gráfico da função f : R  R,
2
definida por f(x) = ax + bx + c, com a≠0, tem seu
vértice no ponto
(1, -16) e sua interseção com os
eixos coordenados contém um ponto cuja
ordenada é y = -15. Para esta função, f(-2) é igual a
A) -3.
B) -5.
C) -7.
D) -9.
Gabarito
1
2
B
B
11 12
B
A
21 22
A
B
3
C
13
C
23
C
4
B
14
D
24
B
5
B
15
D
25
C
6
B
16
D
26
C
7
C
17
D
8
D
18
D
9
C
19
A
10
A
20
D