Aula 2- Função exponencial e logarítma (157

FUNÇÃO EXPONENCIAL
DEFINIÇÃO:
Chama-se função exponencial de base a, com a pertencente aos R*+ - {1}, a função f: R →R*+ definida
por:
f(x) = ax
Exemplo 1:
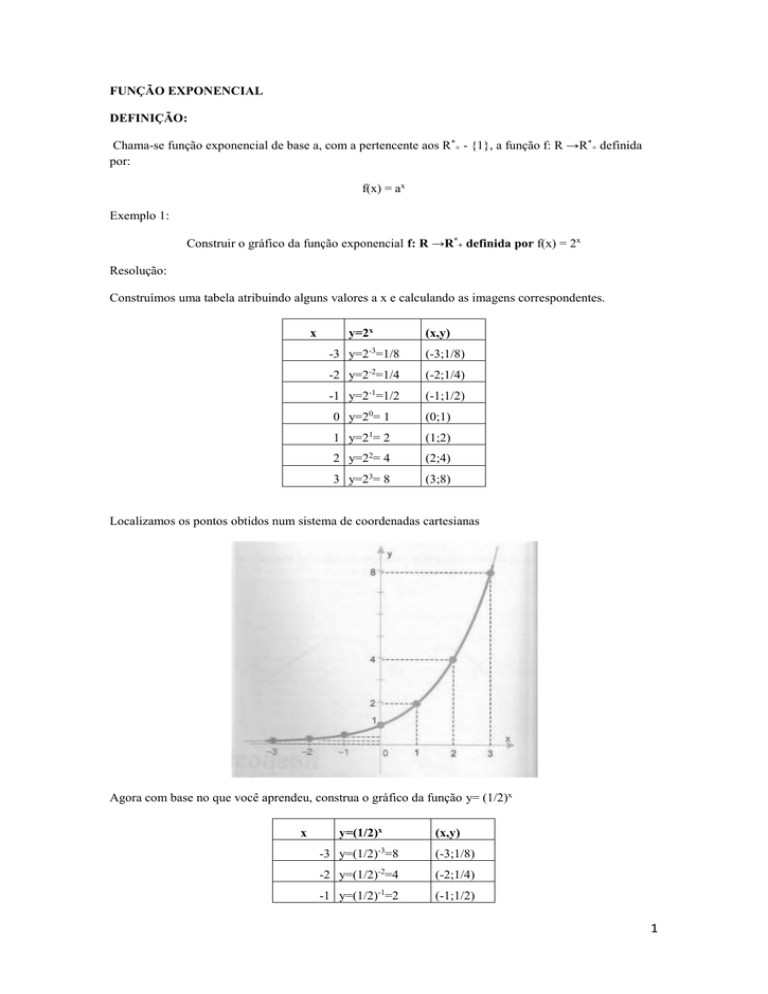
Construir o gráfico da função exponencial f: R →R*+ definida por f(x) = 2x
Resolução:
Construímos uma tabela atribuindo alguns valores a x e calculando as imagens correspondentes.
x
y=2x
(x,y)
-3
-3 y=2 =1/8
(-3;1/8)
-2 y=2-2=1/4
(-2;1/4)
-1
-1 y=2 =1/2
0 y=20= 1
1
(-1;1/2)
(0;1)
1 y=2 = 2
(1;2)
2 y=22= 4
(2;4)
3 y=23= 8
(3;8)
Localizamos os pontos obtidos num sistema de coordenadas cartesianas
Agora com base no que você aprendeu, construa o gráfico da função y= (1/2)x
x
y=(1/2)x
-3
(x,y)
-3 y=(1/2) =8
(-3;1/8)
-2 y=(1/2)-2=4
(-2;1/4)
-1
-1 y=(1/2) =2
(-1;1/2)
1
0 y=(1/2)0= 1
1
(0;1)
1 y=(1/2) = 1/2
(1;2)
2 y=(1/2)2= ¼
(2;4)
3
3 y=(1/2) = 1/8
(3;8)
Demonstra-se que:



O gráfico da função exponencial está sempre acima do eixo x, pois a x>0, para todo x pertencente
aos Reais
O gráfico da função exponencial sempre intercepta o eixo y no ponto (0,1), pois a 0=1
Se a>1 a função exponencial é estritamente crescente e se 0<a<1 a função exponencial é
estritamente decrescente.
PROPRIEDADES DE POTÊNCIA COM EXPOENTE REAL
1)
2)
3)
4)
5)
ax. ay= ax+y
(ax)y= axy
(ab)x= ax. bx
Se a>1 e x<y, então ax<ay
Se 0<a<1 e x<y, então ax>ay
Exercícios:
1) Resolva a equação (1/3)x= 27
2) Resolva a equação 3x=1= 729
FUNÇÃO LOGARÍTMICA
Definição:
Chama-se logaritmo de um número N> 0 numa base a, com a>0 e a diferente de 1, o expoente α deve
elevar a base para que a potência obtida seja igual a N.
LogaN = α tal que aα= N
O número N é chamado logaritmando ou antilogarítmo, a é a base e α é o logaritmo.
Exercício:
3
1) Determinar o logaritmo de√32 na base 2 √2
PROPRIEDADE DOS LOGARÍTMOS:
1)
2)
3)
4)
loga(M.N) = loga M+ logaN
loga(M/N) = loga M- logaN
loga (Nm)= m. logaN
𝑚
loga ( √𝑁 ) = 1/m. logaN para m pertencente ao conjunto dos nu,Eros naturais
MUDANÇA DE BASE
logaN = log N / log a
2
Exercícios:
Calcule os logarítmos.Para alguns casos use logab =2, logac= 3.
1)
2)
3)
4)
loga(a.b/c)
2
loga( a3. √𝑏/ √𝑐 )
log4/25 625/16
log0,00160,008
FUNÇÃO LOGARÍTMA
Chama-se função logarítma de base a, com a >0 e a diferente de 1. Essa função é definida por f: R *+ →R
f(x)= logax
Exemplo:
Construa o gráfico de f(x) = log2 x
y= log2 x
x
(x,y)
1/8 y= log2 (1/8)= -3
(1/8;-3)
1/4
y= log2 (1/4)= -2
(1/4;-2)
1/2
y= log2 (1/2)=-1
(1/2;-1)
1 y= log2 1=0
(1,0)
2 y= log2 2=1
(2;1)
4 y= log2 4=2
(4;2)
8 y= log2 8=3
(8;3)
3
EXERCÍCIO: Construa o gráfico de f(x) = log1/2 x
Demonstra-se que:
1) O gráfico da função logarítmica está sempre à direita do eixo y, pois seu domínio é são o
conjunto dos números reais positivos excluindo-se o 0
2) O gráfico sempre intercepta o eixo x no ponto (1,0), pois log a 1=0
3) Se a>1 a função é crescente
4) Se 0<a <1 a função é decrescente
5) A função logarítmica é inversa da função exponencial e vice e versa e os gráficos são simétricos
em relação à bissetriz dos quadrantes ímpares que é a reta y=x.
O NÚMERO REAL e IRRACIONAL
Esse número foi introduzido por Euler e é o limite da sequência:
( (1+1/1)1 + ((1+1/2)2 +(1+1/3)3 +(1+1/4)4 ,...., (1+1/n)x ,...)
Quando x cresce indefinidamente.
1 𝑥
e = lim (1 + ) = 2,7182818284590453.... e portanto e é aproximadamente 2,71828.
𝑛
𝑥→∞
1 𝑥
Assim, lim (1 + ) = e
𝑥→∞
𝑛
Esse logarítmo tem todas as mesmas propriedades dos outros logarítmos.
LIMITES DE FUNÇÕES EXPONENCIAL E LOGARÍTMICA
EXEMPLO: Suponha que a>1. Calcule os limites
lim (𝑎) 𝑥 = + ∞
𝑥→+∞
4
lim (𝑎) 𝑥 = 0
𝑥→−∞
lim log 𝑎 𝑥
𝑥→−∞
lim log 𝑎 𝑥
𝑥→𝑂+
DERIVADAS DE FUNÇÕES EXPONENCIAL E LOGARÍTMICA
𝒏
Derivadas de xn e √𝒙
Teorema: Seja n ≠0 um natural. São válidas a fórmulas de derivação
a) f(x) = xn →f´(x)= nxn-1
b) f(x) = x-n →f´(x)= -nx-n-1 , com x≠0
c) f(x) = x1/n →f´(x)= 1/nx1/n-1
Derivadas de ex e ln x
a) f(x) = ex →f´(x)= ex
b) g(x) = lnx →g´(x)= 1/x, x>0
5