GEOMETRIA BÁSICA 2011-2
GGM00161-TURMA M2
Dirce Uesu Pesco
Geometria Espacial
17/11/2011- Poliedros
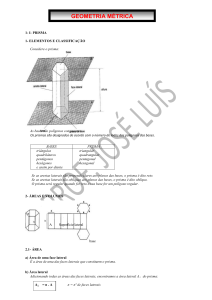
POLIEDROS CONVEXOS
Poliedro Convexo:
Considere um número finito n, n 4, de polígonos planos convexos ( ou região
poligonal convexa) tais que:
a) dois polígonos não estão em um mesmo plano;
b) cada lado do polígono é comum a dois e somente dois polígonos;
c) o plano de cada polígono deixa os demais num mesmo semi-espaço.(condição de convexidade)
Nessas condições, ficam determinados n semi-espaços , cada um dos quais
tem origem no plano de um polígono e contem os restantes.
A interseção desses semi-espaços é chamado Poliedro convexo.
POLIEDROS CONVEXOS
Quais dos exemplos abaixo são poliedros, poliedros convexos ?
POLIEDROS CONVEXOS
Quais dos exemplos abaixo são poliedros, poliedros convexos ?
a)poliedro, não convexo
d)Poliedro convexo
b) não é poliedro
e) poliedro convexo
c) poliedro não convexo
f) não é poliedro
f) não é poliedro
POLIEDROS CONVEXOS
Exercício: Desenhe outros exemplos de poliedros convexos.
POLIEDROS CONVEXOS
Elementos do poliedro convexo:
Faces: são os polígonos;
Arestas: são os lados dos polígonos;
Vértices : sãos os vértices dos polígonos;
Ângulos : são os ângulos dos polígonos.
PROPRIEDADE DE POLIEDROS CONVEXOS
Teorema de Euler
Para todo poliedro convexo vale a relação:
V A F 2
onde
V é o número de vértice, A é o número de arestas e F o número de faces do
poliedro convexo.
Exemplo: Verifique se vale a relação de Euler para os poliedros abaixo:
PROPRIEDADE DE POLIEDROS CONVEXOS
Teorema de Euler
Para todo poliedro convexo vale a relação:
V A F 2
onde
V é o número de vértice, A é o número de arestas e F o número de faces do
poliedro convexo.
Exemplo: Verifique se vale a relação de Euler para os poliedros abaixo:
a)
b)
PROPRIEDADE DE POLIEDROS CONVEXOS
Exemplo 2 : Vale a relação de Euler para os poliedros abaixo?
a)
b)
PROPRIEDADE DE POLIEDROS CONVEXOS
Exemplo 2 : Vale a relação de Euler para os poliedros abaixo?
a)
b)
Poliedro Euleriano: poliedros para os quais vale a relação de Euler.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exemplo 2 : Vale a relação de Euler para os poliedros abaixo?
a)
b)
Poliedro Euleriano: poliedros para os quais vale a relação de Euler.
Todo poliedro convexo é euleriano, mas nem todo poliedro euleriano é convexo.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2)
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2) V 10
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2) V 10
Logo o prisma é pentagonal.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
Si (5 2).180o 540o
Base pentagonal
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
S (V 2) 4r
é:
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
Si (5 2).180o 540o
Base pentagonal
S 2 540o 5 360o 2880o
PROPRIEDADE DE POLIEDROS CONVEXOS
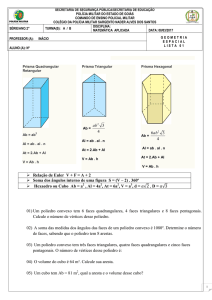
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais,
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60o
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
Al 4 Aparalelogramo
5 3
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
Al 4 Aparalelogramo Al 4 3. 5 3 30 3 cm 2
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
Al 4 Aparalelogramo Al 4 3. 5 3 30 3 cm 2
2
Exercício: encontre a área total e o volume do prisma
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Exercício : Encontre a área total e o volume do prisma.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Exercício : Encontre a área total e o volume do prisma.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício: Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Encontre a área total e o volume do prisma.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício: Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Encontre a área total e o volume do prisma.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício: Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Encontre a área total e o volume do prisma.
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício: Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Encontre a área total e o volume do prisma.
POLIEDROS
REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
POLIEDROS
REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
Teorema: Existem apenas cinco poliedros regulares.
http://www.uff.br/cdme/platonicos/platonicos-html/solidos-platonicos-br.html
POLIEDROS
REGULARES
Definição:
Poliedro regular é um poliedro convexo em que as faces são polígonos regulares congruentes e que em todos os vértices concorrem o mesmo número
de arestas.
Teorema: Existem apenas cinco poliedros regulares.
i) 4 faces
ii) 6 faces
iii) 8 faces
ii) cubo (hexaedro regular),
i) tetraedro regular,
iv) 12 faces
v) 20 faces
iv) dodecaedro regular ,
iii) octaedro regular,
v) icosaedro
regular
http://www.uff.br/cdme/platonicos/platonicos-html/solidos-platonicos-br.html
POLIEDROS
REGULARES
Exercício:
Preencha a tabela abaixo:
Poliedro regular
V
A
tetraedro
4
6
cubo (hexaedro regular)
8
12
F
n-arestas
em cada
face
m-arestas
em cada
vértice
4 faces
3
3
6 faces
4
3
octaedro
8 faces
dodecaedro
12 faces
icosaedro
20 faces
POLIEDRO CONVEXO E REGULAR
Área e Volume
Exercícios:
Livro texto, capítulos: Poliedro convexo e Regular .