ω ϕ α β α β β α ϕ ω ϕ ω ω ω ϕ π π π

MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
1. Um pêndulo simples consiste de uma massa
presa a uma corda de 0.6 m que oscila em MHS. A sua
máxima velocidade é 0.4 m/s. Determine:
(a) O período e sua máxima amplitude, em graus.
(b) sua máxima aceleração tangencial.
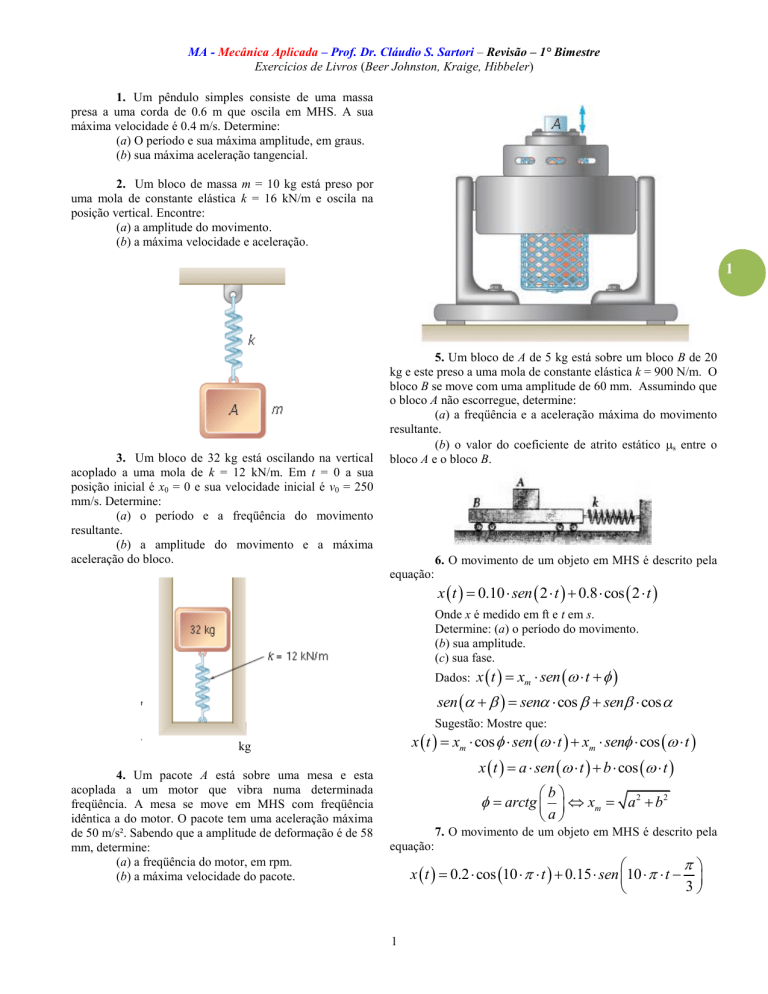
2. Um bloco de massa m = 10 kg está preso por
uma mola de constante elástica k = 16 kN/m e oscila na
posição vertical. Encontre:
(a) a amplitude do movimento.
(b) a máxima velocidade e aceleração.
1
3. Um bloco de 32 kg está oscilando na vertical
acoplado a uma mola de k = 12 kN/m. Em t = 0 a sua
posição inicial é x0 = 0 e sua velocidade inicial é v0 = 250
mm/s. Determine:
(a) o período e a freqüência do movimento
resultante.
(b) a amplitude do movimento e a máxima
aceleração do bloco.
5. Um bloco de A de 5 kg está sobre um bloco B de 20
kg e este preso a uma mola de constante elástica k = 900 N/m. O
bloco B se move com uma amplitude de 60 mm. Assumindo que
o bloco A não escorregue, determine:
(a) a freqüência e a aceleração máxima do movimento
resultante.
(b) o valor do coeficiente de atrito estático s entre o
bloco A e o bloco B.
6. O movimento de um objeto em MHS é descrito pela
equação:
x  t   0.10  sen  2  t   0.8  cos  2  t 
Onde x é medido em ft e t em s.
Determine: (a) o período do movimento.
(b) sua amplitude.
(c) sua fase.
Dados:
x  t   xm  sen   t   
sen      sen  cos   sen  cos 
Sugestão: Mostre que:
x  t   xm  cos   sen   t   xm  sen  cos   t 
kg
4. Um pacote A está sobre uma mesa e esta
acoplada a um motor que vibra numa determinada
freqüência. A mesa se move em MHS com freqüência
idêntica a do motor. O pacote tem uma aceleração máxima
de 50 m/s². Sabendo que a amplitude de deformação é de 58
mm, determine:
(a) a freqüência do motor, em rpm.
(b) a máxima velocidade do pacote.
x  t   a  sen   t   b  cos   t 
b
 
  arctg    xm  a 2  b 2
a
7. O movimento de um objeto em MHS é descrito pela
equação:


x  t   0.2  cos 10    t   0.15  sen 10    t  
3

1
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
Onde x é medido em ft e t em s.
Determine: (a) o período do movimento.
(b) sua amplitude.
(c) sua fase.
Dados:
9. No sistema da figura, ka = 50 kN/m, kb =
100 kN/m e kc = 150 kN/m. O bloco tem uma massa de
50 kg. Determine o período de vibração.
x  t   xm  sen   t   
sen      sen  cos   sen  cos 
8. Nos sistemas vibrantes abaixo,
determine:
(a) o período e a freqüência.
(b) a máxima compressão da mola.
(c) a máxima velocidade e a máxima aceleração.
8.1
8.2
k = 12 kN/m
8.3
2
10. Denotando por est a deflexão estática da viga sob
uma dada carga, mostre que a frequência de vibração da carga é:
8.4
8.5
f 
1
2
g
 est
11. Se h = 700 mm e d = 500 mm e cada mola tem uma
constante k = 600 N/m, determinar a massa m para que o período
de pequenas oscilações seja:
(a) 0,50 s, (b) infinito. Negligenciar a massa da haste e
assumir que cada mola pode actuar em ambas tensão ou
compressão.
2
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
Se deslocarmos o cursor 63.5 mm para baixo da sua posição de
equilíbrio, determine
(a) o tempo gasto pelo cursor para ele se mover 50.8
mm para cima
(b) suas correspondentes velocidade e aceleração.
15. Um motor pesando 1750 N está apoiado por 4
molas, cada uma com constante elástica de 150 kN/m. O
desbalanceamento do rotor é equivalente a uma massa de 30 g
localizada a 0.15 m do eixo de rotação. Sabendo que o motor é
obrigado a mover-se verticalmente, determine:
(a) a freqüência em rpm que ocorrerá a ressonância.
(b) a amplitude da vibração do motor na freqüência de
1200 rpm.
12. O cursor de 3.00 kg repousa sobre, mas não
está preso a, a mola ilustrada. O cursor é pressionado 0.050
m e liberado. Se o movimento que se segue é harmônico,
determine
(a) o valor máximo permissível da constante k da
mola
(b) a posição, a velocidade e a aceleração do
cursor 0.15 s após ele ter sido solto.
16. Um corpo preso a uma mola, de massa 3kg, oscila
com amplitude 4 cm e período 2s.
(a) Qual a energia mecânica total do sistema?
(b) Que velocidade máxima tem o corpo?
(c) Em que posição x1 a velocidade é metade da
velocidade máxima?
13. Um cursor de 4.00 kg está preso a uma mola
de constante k = 800N/m como ilustrado. Se a ele é dado
um deslocamento de 40 mm para baixo de sua posição de
equilíbrio, determine
(a) o tempo necessário para o cursor mover-se 60
mm para cima e
(b) a sua aceleração correspondentes.
17. O movimento do pistão no interior do motor de um
carro é aproximadamente um MHS.
(a) Sabendo que o percurso (o dobro da amplitude) é
igual a 0.100m e que o motor gira a 3500 rpm, calcule a
aceleração do pistão no ponto final do percurso.
(b) Sabendo que a massa do pistão é 0.45 kg, qual é a
força resultante exercida sobre ele nesse ponto?
(c) Calcule a velocidade e a energia cinética do pistão
no ponto médio do percurso.
(d) Qual é a potência média necessária para acelerar o
pistão do repouso até a velocidade calculada no item (c)?
(e) Se o motor gira com 7000 rpm, quais são as
respostas dos itens (b), (c) e (d)?
14. Um cursor de 1.36 kg está ligado a uma mola
da constante k = 876 N/m como ilustrado no exercício 13.
3
3
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
18. Um cilindro de 5 kg está suspenso por uma
mola de constante elástica 320 N/m e está submetido a uma
força periódica vertical
°
F  Fm  sen   t  , onde Fm =
5
15
45
14 N. Determine a amplitude do movimento do cilindro
para:
(a)  = 6 rad/s (b)  = 12 rad/s.
19. Um pêndulo simples consiste de uma massa m
conectada a um fio de comprimento l que oscila em um
plano vertical com um período de 1.3 s. Assumido que o
movimento é um MHS e que sua máxima velocidade vale
0.4 m/s, determine:
(a) a amplitude do movimento em graus;
(b) a máxima aceleração do corpo.
T(s)
22. Um pequeno corpo de massa m está preso a um fio
de comprimento l = 1.2 m quando é solto a partir do repouso a
um ângulo
 A  50 . Sabendo que d = 0.6 m, determine:
(a) o tempo requerido para a bola retornar ao ponto A.
(b) a amplitude máxima
C .
23. O sistema abaixo começa a oscilar a 40 mm de sua
posição de equilíbrio. Determine o período de oscilação.
20. Um pêndulo simples de comprimento l = 40 in
é solto a partir do repouso de um ângulo de 5°. Assumindo
que o movimento é um MHS, determine, após 1.2 s:
(a) o ângulo ;
(b) a velocidade e a aceleração nesse instante.
21. Considerando lançamentos a grandes ângulos,
o período é dado por:
T  2
l
g
2
  1 
2
1    sen
2
  
 
0
2
 1 3 
4

 sen
2

4


2
 
0
2
 1 3  5 
6

 sen
2

4

6


2
 
0
2
24. No sistema, a oscilação é 2 in a partir da posição de

  equilíbrio. Em cada caso, determine o período de oscilação, a
 freqüência, a máxima velocidade e a máxima aceleração.
Determine o período, completando a tabela:
4
4
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
(a)
(b)
27. Quando se aumenta lentamente a velocidade de um
motor, suportado por molas, de 300 para 500 rpm, a amplitude
de vibração devida ao desbalanceamento do rotor aumenta de
1.5 mm para 6 mm. Determine a velocidade (freqüência) para a
qual ocorrerá a ressonância.
28. Um cilindro de massa m suspenso por uma mola de
constante k está sob ação de uma força periódica vertical de
módulo
F  Fm  sen   t  . Determine a faixa dos valores de
 para os quais a amplitude de vibração excede duas vezes a
deflexão estática produzida por uma força de módulo Fm.
25. Um motor de velocidade variável está
rigidamente preso à viga BC. O motor está ligeiramente
desbalanceado e faz a viga vibrar com freqüência angular
igual à velocidade do motor.
Quando a velocidade do motor é menor que 450
rpm ou mais que 900 rpm, observa-se que um pequeno
objeto colocado em A permanece em contato com a viga.
Para velocidades entra 450 e 900 rpm o objeto "dança" e
realmente perde o contato com a barra. Determine a
amplitude do movimento de A quando a velocidade do
motor é:
(a) 450 rpm, (b) 900 rpm.
29. Um pacote B é colocado sobre uma mesa C que
oscila em MHS com uma frequência de 3 Hz. Sabendo que o
coeficiente de atrito estático entre o pacote e a mesa é s = 0.40,
determine a maior amplitude de forma que o pacote não deslize
sobre a mesa.
30. Um pêndulo simples composto por uma massa m e
um fio de comprimento l = 40 in é abandonado a um ângulo  =
50. Assumindo MHS, determine após 1.5 s:
(a) o ângulo ( t = 1.5s );
(b) o valor da velocidade e da aceleração nesse instante.
26. Um motor de massa M = 400kg é suportado
por 8 molas, cada uma com constante elástica de 20 kN/m e
pode-se mover verticalmente. O desbalanceamento do rotor
é causado por uma massa m de 20g colocada a r = 30 mm
do eixo de rotação. Numa frequência de vibração de f =
5000 rpm, determine:
(a) a frequência de ressonância f0.
(a) a máxima amplitude de força devida ao
desbalanceamento;
(b) a deformação máxima xm causada pelo
desbalanceamento?
5
5
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
31. O período de vibração do sistema indicado na
figura é 1.5 s. Se substituirmos o cilindro B por outro de
peso igual a 17.8 N, o período passará a ser de 1.6 s.
Determinar
(a) a massa do cilindro A e
(b) a constante da mola.
34. O prumo de um pêndulo simples de comprimento l
= 40 in é liberado a partir do repouso, quando θ = 5 °.
Assumindo movimento harmônico simples, determine
1.6 s após o lançamento (a) o ângulo θ, (b) a magnitude da
velocidade e aceleração do prumo.
3 lb(f) = 13.3N
32. O período de vibração para o barril flutuante
em água salgada é 0.58 s quando o barril está vazio e 1.8 s,
quando ele é preenchido com 55 litros de petróleo bruto.
Sabendo-se que a densidade do petróleo é de 900 kg/m3,
determinar (a) a massa do cilindro vazio, (b) a densidade da
água salgada, s.
Dica:. A força da água na parte inferior do tambor
pode ser modelada como uma mola com uma
constante
k  s  g  A .
35. Um motor de 125 kg é suportado por uma viga leve
horizontal. O desbalanceamento do rotor é equivalente a uma
massa de 25 g localizada a 200 mm do eixo de rotação. Sabendo
que a deflexão estática da viga devida ao peso do motor é 6.9
mm, determine
(a) a velocidade (frequencia, em rpm) em que
ocorrerá a ressonância
(b) a amplitude do estado estacionário do motor na
freqüência de 720 rpm.
33. Na mecânica dos materiais, é conhecido que,
para uma barra de secção transversal constante de uma
carga estática P aplicada na extremidade B irá causar um
B 
P  L3
3 E  I
desvio dado por:
onde L é o comprimento da viga, E é o módulo de
elasticidade, e I é o momento de inércia da área da secção
transversal do feixe.
Sabendo que:
L = 10 ft,
lb
E  29 106 2
in e
36. O sistema da figura oscila com período 0.75 s.
(a) Encontre a massa m do bloco menor.
(b) Determine o mínimo valor do coeficiente
de atrito estático entre os blocos de forma que não haja
escorregamento entre eles.
I  12.4in4 , determine:
(a) a constante da mola equivalente da viga,
(b) a freqüência de vibração de um bloco de 520 lb
anexado ao fim B do mesmo feixe.
6
6
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
37. No sistema mola-suporte para a plataforma de
pesagem, foi projetado que a frequência de vibração
vertical livre na condição sem carga não deve ultrapassar 3
ciclos por segundo. (a) Determinar a máximo constante da
mola aceitável k para cada um dos três molas idênticas. (b)
Para esta constante da mola, qual seria a frequência natural
de vibração vertical da plataforma carregada pelo caminhão
de 40 toneladas ?
Dados:
Constantes
1 kips = 103 ips = 103.9.81. 0.45359237 N
(Kilo Pounds)
1 ft = 0.3048 m = 12 in
1lb = 0.45359237kg
1lb (força) = 4.449 N
g = 9.81m/s2 = 386.22 in/s2 = 32.19 ft/s2
1cv  735W  1HP  1.014CV
1 m3 = 1000 L = 264.172 gal
MHS
7
 x  cos 0  t   
xH  t    m
 xm  sen 0  t   
38. Uma mulher está no centro de uma placa fina e
provoca uma deflexão de 0.9 in. Se ela flexiona seus pés
um pouco a fim de provocar uma vibração vertical, qual é a
frequência do movimento? Suponha resposta elástica da
placa e negligenciar sua massa relativamente pequena.
v 
xm  x   0 
 
2
2
0
(Amplitude máxima)

   x0 
v0 
   arctg 

   x0 
 v0 
  arctg  
(Fases)
k
0 
m
39. O pára-choque de um carro possui um sistema
de absorção de energia; quando inicialmente não deformado
ele tem uma constante de mola equivalente de 3000 lb/in.
Se o carro se aproxima de uma parede maciça com uma
velocidade de 5 mi/h determinar (a) a velocidade do carro
em função do tempo durante o contato com
a parede, onde é o começo do impacto, e (b) a deflexão
máxima do pára-choques.
2 
T
Oscilações forçadas
   2   f   
40. Um pedaço 3 kg de massa de vidraceiro é
descartado a 2 m sobre o bloco de 28 kg inicialmente
estacionário, o qual é suportado por quatro molas, cada um
dos quais tem uma constante k = 800 N/m. Determinar o
deslocamento x como uma função do tempo durante a
vibração resultante, em que x é medido a partir da posição
inicial do bloco tal como apresentado.
xm 
Fm
k
2
1 2
0
0 
 xm 
m
 
1 

 0 
2

k
 f0  0
m
2
(frequência de ressonância)
7
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
n
Gabarito dos Exercícios
Resposta
n
Resposta
(a) T  1.13s  f  0.884Hz
(a) T = 1.55 s; m  9.45
0
1
9
(b) vm  0.2453  am  9.81
(a) T  0.3245s  f  3.08Hz
3
4
5
m
s2
10
11
m
(b) xm  0.01291  am  4.841 2
s
(a) f  280.4rpm
m
(b) vm  18.7329
s
m
(a) f  5.72 Hz  am  2.16 2
s
12
13
14
15
7
17
  43.025
0
(b) xm  0.01073m
(b) xm  0.0123m
m
 EC  75.564 J
s
 17631.59W  23.98cv  23.66hp
(b) v  18.326
18
19
(a) x  9.85cm (b) x  9.98cm
(a) m  0.197rad  11.290
20
m
s2
(a)  (t  1.2)  0.06232rad  3.570
m
(b) v(t  1.2)  0.6
s
21
22
(b) xm  0.0429m
m
m
 am  9.81 2
s
s
(a) T  0.3s  f  3.33Hz
23
(b) xm  0.02237m
(c) vm  0.4684
m
s2
(b) am  9.34
(c) vm  0.6488
8.4
m
s
(c) x  3.46cm
(b) vm  0.126
(c) P1Pistão
m
m
(c) vm  0.348  am  9.81 2
s
s
(a) T  0.4156s  f  2.406Hz
8.3
(a) 554rpm (b) xm  3.2  10 m
(a) a  6716.814
m
m
(c) vm  0.3244  am  9.81 2
s
s
(a) T  0.223s  f  4.484Hz
8.2
s2
5
0
(a) T  0.20779s  f  4.8124Hz
8.1
m
m
 (c) 4 2 
s
s
(a) 0.05857s (b) 1.6059 m  (c) 54.27 m 
16
(a) T  0.2s
(b) xm  0.102m
(c)
(a) 0.15s (b) 0.49
8
(a) E  2.37 102 J
(a) xm  0.806m
(b)   82.87
(a) 3.56kg (b) 43.7kg
Resolvido em sala de aula.
s
(b) s  0.22
6
in
in
 am  39.36 2
s
s
T  0.1038s
1
g
f 
2  est
(c) vm  7.089
(a) xm  6.13mm
2
(b) xm  1.277in
8.5
m
(b) am  1.616 2
s
m
m
 am  9.81 2
s
s
8
Complete a tabela.
0
(a) TABCBA  1.8757s (b) mC  7.07
0.3613 s
MA - Mecânica Aplicada – Prof. Dr. Cláudio S. Sartori – Revisão – 1° Bimestre
Exercícios de Livros (Beer Johnston, Kraige, Hibbeler)
n
Resposta
rad
s
T  0.2064s  f  4.84Hz
(a)   30.43
vm  60.9
24
25
in
in
 am  1852 2
s
s
27
29
30
31
32
(b) Fm  164.49 N (c) xm  1.5 106 m
783 rpm
k
3k
 
2m
2m
11 mm
(a)  (t  1.5)  0.0024rad  0.140
in
s
in
(c) a(t  1.5s)  0.106 2
s
(b) v(t  1.5s)  3.71
N
m
kg
(a) mb = 21.7 kg(b)  s  1011 3
m
(a) mA  1.973kg (b) k  87.6
(a) ke = 624.3 lb/in
(b) f n  3.43Hz
(a)   1.2880
(b)
34
(a) v  t   88  cos  21.5  t in s 
(b) xmax  4.09in
x  t   9.3  103  1  cos10.16  t 
9
(a) f 0  135rpm
v  0.874
f n  3.3Hz
59.7  103  sen10.16  t  m 
in
in
vm  30.45  am  463.60 2
s
s
(a) x  f  450rpm   4.417mm
33
38
40
rad
s
T  0.4126s  f  2.42Hz
(b)   15.225
28
(a) 360 rpm (b) 0.71 m
(a) m = 2.54 kg (b) s = 0.358
(a) k  474 kN m (b) f n  0.905Hz
39
(b) x  f  900rpm   1.1044mm
26
35
36
37
ft
s
v2
ft
 l  2  0.22894 2
l
s
ft
at  l   0.72433 2
s
ft
a  aT2  an2  a  0.9597 2
s
an 
9