FUNÇÃO EXPONENCIAL Edir DOC

PROF. JACSON
E.E. EDIR PAULINO ALBUQUERQUE Reposição de Matemática 10/2013
FUNÇÃO EXPONENCIAL
Chamamos de função exponencial a toda função do tipo f(x) = ax, definida para todo x real com a > 0 e
a ≠ 1.
Exemplo:
a) f(x) = 2x
1
b f(x) = (2)x
Conceito de função exponencial
A expressão “crescimento exponencial” refere-se a um crescimento muito rápido.
Assim, a função exponencial possui múltiplas aplicações:
 na área financeira, em tabelas progressivas a juros fixos;
 no crescimento populacional;
 em biologia, no crescimento de alguns vegetais, entre outros.
Gráfico da função exponencial:
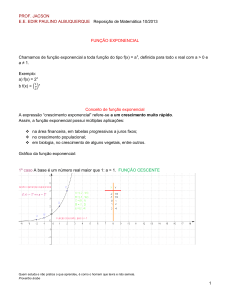
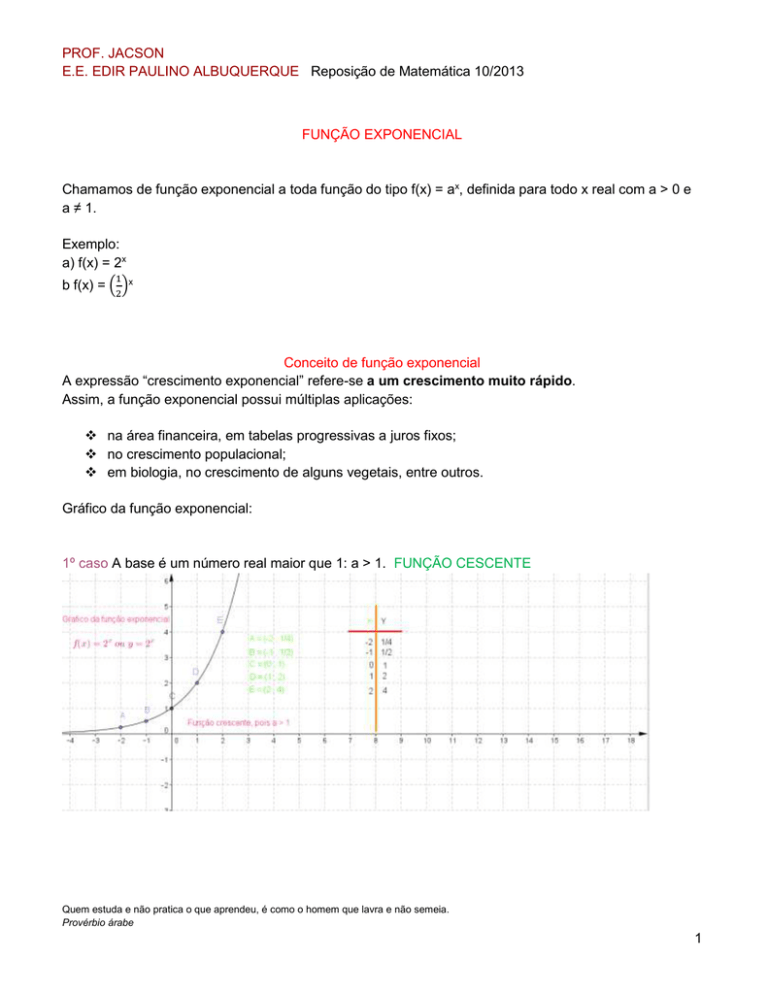
1º caso A base é um número real maior que 1: a > 1. FUNÇÃO CESCENTE
Quem estuda e não pratica o que aprendeu, é como o homem que lavra e não semeia.
Provérbio árabe
1
PROF. JACSON
E.E. EDIR PAULINO ALBUQUERQUE Reposição de Matemática 10/2013
2º caso A base é um número real maior que 0 e menor que 1: 0 < a < 1. FUNÇÃO DECRESCENTE
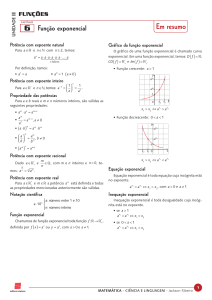
Características da função exponencial
 A curva da função f(x) = ax passa pelo ponto (0 , 1);
 O seu domínio é o conjunto dos reais D = R;
 O seu conjunto imagem é Im = 𝑅+∗ ;
 A função é crescente para a base a maior que 1 (a > 1);
 A função é decrescente para a base a maior que 0 e menor que 1 (0 < a < 1).
ax
ax = ax + x ⇒ Multiplicação de potência de mesma base, conserva-se a base e soma-se os
expoentes;
ax : ax = ax - x ⇒ Divisão de potência de mesma base, conserva-se a base é subtrai-se os expoentes;
(ax)x = ax
ax
x
⇒ Potência de potência, conserva-se a base e multiplicam-se os expoentes;
bx = ( a * b)x ⇒Multiplicação de potencia de mesmo expoente, multiplica-se as bases e conserva-se
o expoente.
ax
=
bx
a
(b)x ⇒Divisão de potência de mesmo expoente, divide-se as bases e conserva-se o
expoente.
Antes de ir para a resolução, aconselho a fazer uma revisão de alguns tópicos importantes para os
estudos das funções exponenciais.
Quem estuda e não pratica o que aprendeu, é como o homem que lavra e não semeia.
Provérbio árabe
2
PROF. JACSON
E.E. EDIR PAULINO ALBUQUERQUE Reposição de Matemática 10/2013
Pesquise os “Conceitos Básicos Sobre Potenciação” No http://www.youtube.com/ você pode te ajuda,
pesquise.
- Potenciação;
- Expoente inteiro não negativo;
- Expoente inteiro negativo;
- Propriedades das potencias, cujo expoente é um número inteiro;
- Expoente racional;
- Propriedades das potencias, cujo expoente é um número racional;
- Potência cujo expoente é um número irracional.
Estes vídeos podem ajudar:


http://youtu.be/5tV-6W5_TLA
http://youtu.be/20lm2lx6r0g
Elabore a resolução:
1) Um determinado tipo de vegetal cresce dobrando a sua altura mensalmente. Sabendo que sua altura
é 1 mm, determine a expressão exponencial altura y(mm) em função do tempo e construa o gráfico
cartesiano dessa função;
Obs.: Neste site você pode obter ajuda para entender a resolução desse exercício:
http://qi-epitacio-ensino-medio.blogspot.com.br/2012/06/trabalho-de-matematica-carlos-valerio-3.html
2) Esboçar o gráfico da função dada por y = 3x + 1, classificando a função em crescente ou
decrescente;
Este vídeo pode ajudar:
 http://youtu.be/zcYhZLK8c_c
 http://youtu.be/7_T2JGEqZgg
Leia o texto desta página e responda as questões abaixo:
3) Onde podemos usar funções exponenciais?
4) Na função f(x) = 2x + 3, determine quem é a base.
5) No caso da base de uma função ser um número maior que 1 o que isso significa? E se a base for um
número entre 0 e 1, essa função será crescente ou decrescente?
6) A qual tipo de crescimento refere-se uma função exponencial?
Bons estudos!
Quem estuda e não pratica o que aprendeu, é como o homem que lavra e não semeia.
Provérbio árabe
3
PROF. JACSON
E.E. EDIR PAULINO ALBUQUERQUE Reposição de Matemática 10/2013
Quem estuda e não pratica o que aprendeu, é como o homem que lavra e não semeia.
Provérbio árabe
4