6 Função exponencial Em resumo

UNIDADE I I
FUNÇÕES
CA P Í T U LO
Em resumo
6 Função exponencial
Potência com expoente natural
Para a ∈ e n ∈ com n ≥ 2, temos:
a =
a ⋅ 
a⋅ a
⋅ a
⋅ a
⋅ a ⋅…
⋅a
n
n fatores
Por definição, temos:
• a1 = a
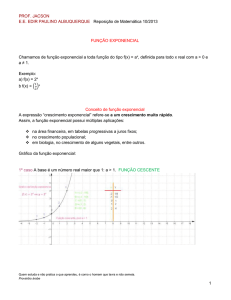
Gráfico da função exponencial
O gráfico de uma função exponencial é chamado curva
exponencial. Em uma função exponencial, temos: D ( f ) = , CD ( f )
D ( f ) = , CD ( f ) = *+ e Im ( f ) = *+ .
•Função crescente: a > 1
• a0 = 1 ( a ≠ 0 )
Potência com expoente inteiro
n
Vm&
n
1
 1
Para a ∈* e n ∈, temos: a− n =   = n .
 a
a
Vm'
Propriedade das potências
&
Para a e b reais e m e n números inteiros, são válidas as
seguintes propriedades:
%
m' m& m
x
x1 > x2 ⇔ a 1 > a
• am ⋅ an = am+ n
x2
•Função decrescente: 0 < a < 1
am
= a m− n , a ≠ 0
n
a
m
• ( a ⋅ b) = am ⋅ bm
•
n
Vm'
m
am
 a
•   = m , b ≠ 0
 b
b
( )
• am
n
Vm&
&
= am⋅n
m
m' m& %
Potência com expoente racional
x
x1 > x2 ⇔ a 1 < a
x2
m
Dado a ∈ e
∈, com m e n inteiros e n > 0, ten
m
mos: a n = n am .
Equação exponencial
Potência com expoente real
Equação exponencial é toda equação cuja incógnita está
no expoente.
*
+
Para a ∈*+ e m ∈ a potência am está definida e todas
as propriedades mencionadas anteriormente são válidas.
x
x
a 1 = a 2 ⇔ x1 = x2, com a > 0 e a ≠ 1
Inequação exponencial
Notação científica
 a: número entre 1 e 10
a ⋅10n 
o
n: número inteiro
Inequação exponencial é toda desigualdade cuja incógnita está no expoente.
Função exponencial
Chamamos de função exponencial toda função f:  → *+ ,
definida por f ( x ) = a ou y = a , com a > 0 e a ≠ 1.
x
x
•se a > 1
x
x
a 1 > a 2 ⇔ x1 > x2
•se 0 < a < 1
x
x
a 1 < a 2 ⇔ x1 > x2
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro