Trabalho Computacional de Eletromagnetismo

Trabalho Computacional de Eletromagnetismo
Prof. Antonio Carlos Siqueira de Lima
Julho de 2012
Comentários
Os exercı́cios a seguir possuem solução analı́tica, i.e., há uma expressão fechada que permite representar as grandezas
envolvidas. O objetivo é aplicar os métodos numéricos para a solução do campo e comparação dos erros envolvidos
pela aproximação numérica.
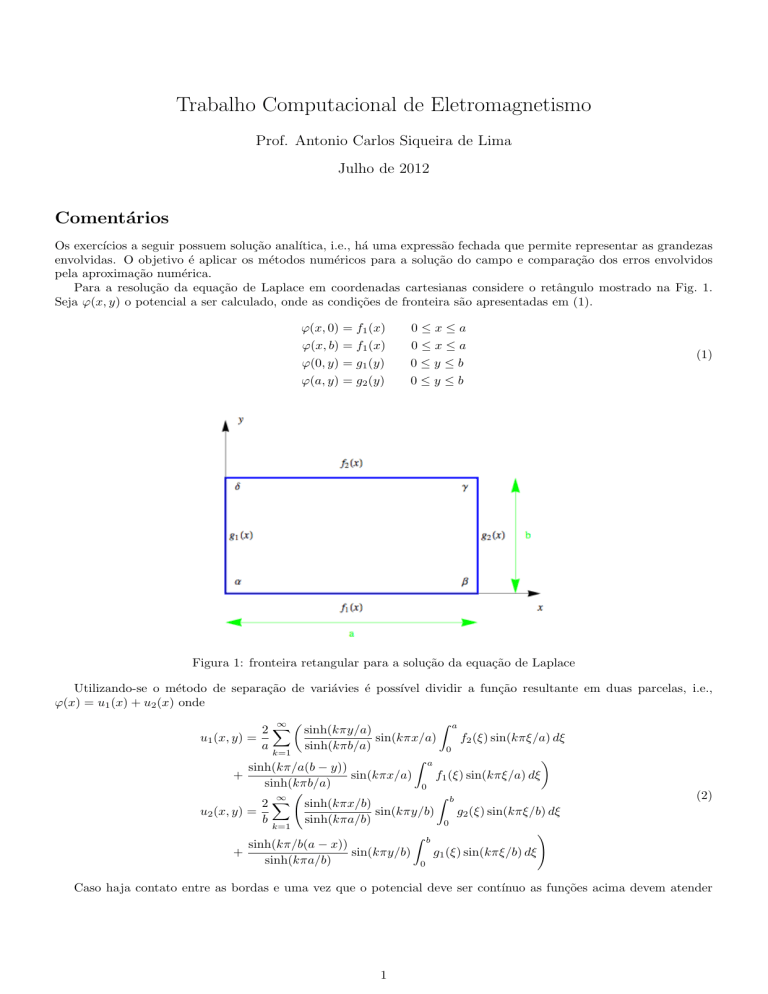
Para a resolução da equação de Laplace em coordenadas cartesianas considere o retângulo mostrado na Fig. 1.
Seja ϕ(x, y) o potencial a ser calculado, onde as condições de fronteira são apresentadas em (1).
ϕ(x, 0) = f1 (x)
0≤x≤a
ϕ(x, b) = f1 (x)
0≤x≤a
ϕ(0, y) = g1 (y)
0≤y≤b
ϕ(a, y) = g2 (y)
0≤y≤b
(1)
Figura 1: fronteira retangular para a solução da equação de Laplace
Utilizando-se o método de separação de variávies é possı́vel dividir a função resultante em duas parcelas, i.e.,
ϕ(x) = u1 (x) + u2 (x) onde
∞
Z a
sinh(kπy/a)
sin(kπx/a)
f2 (ξ) sin(kπξ/a) dξ
sinh(kπb/a)
0
k=1
Z a
sinh(kπ/a(b − y))
+
sin(kπx/a)
f1 (ξ) sin(kπξ/a) dξ
sinh(kπb/a)
0
Z b
∞
2 X sinh(kπx/b)
u2 (x, y) =
sin(kπy/b)
g2 (ξ) sin(kπξ/b) dξ
b
sinh(kπa/b)
0
k=1
!
Z b
sinh(kπ/b(a − x))
+
sin(kπy/b)
g1 (ξ) sin(kπξ/b) dξ
sinh(kπa/b)
0
2X
u1 (x, y) =
a
(2)
Caso haja contato entre as bordas e uma vez que o potencial deve ser contı́nuo as funções acima devem atender
1
também as seguintes condições
f1 (0) = g1 (0) = α
f1 (a) = g2 (0) = β
(3)
f2 (a) = g2 (b) = γ
f2 (0) = g1 (b) = δ
o que leva o potencial a ser definido por
ϕ(x, y) = û1 (x, y) + û2 (x, y) + u0 (x, y)
(4)
onde
1
πy
πx
π(a − x)
πy
πx
π(a − x)
u0 (x, y) =
cos
β sinh
+ α sinh
+ sin
γ sinh
+ δ sinh
sinh(πa/(2b))
2b
2b
2b
2b
2b
2b
(5)
as funções û1 (x, y) e û2 (x, y) diferem daquelas em em (2) apenas pelos coeficientes das integrais conforme mostrado a
seguir.
Z a
(f2 (ξ) − u0 (ξ, b)) sin(kπξ/a)dξ
Z0 a
(f1 (ξ) − u0 (ξ, 0)) sin(kπξ/a)dξ
0
Z
(6)
b
(g2 (ξ) − u0 (a, ξ)) sin(kπξ/b)dξ
0
Z
b
(g1 (ξ) − u0 (0, ξ)) sin(kπξ/b)dξ
0
1
Campos Estacionários
1. Considere a caixa cuja seção transversal é mostrada na Fig. 2. Calcule o potencial no interior da caixa sabe-se
que dois dos lados são mantidos num potencial V e os outros dois aterrados. Obtenha a resposta analı́tica e
plote o resultado final supondo a = 5 cm e b = 2 cm.
y
0
V
V
x
b
0
2a
Figura 2: Caixa condutora
resposta:
φ(x, y) =
∞
n
4V X (−1) cosh [(2n + 1)πx/b]
cos (πy/b(2n + 1))
π n=0 2n + 1 cosh [(2n + 1)πa/b]
(7)
A Fig. 3 apresenta o gráfico da solução apresentada em (7). Uma outra expressão é possı́vel, nesse caso vamos
adotar a origem dos eixos x − y coincidente com o ponto onde o eletrodo vertical com potencial V se une ao
eletrododo horizontal aterrado. Para simplificar a notação consideramos que nesse novo sistema de coordenadas
a = 2a quando referido à Fig. 2. A expressão do potencial é mostrada na (8).
ϕ(x, y) =
∞
4 X sin((2n + 1)πy/b)
[sinh((2n + 1)πx/b) + sinh((2n + 1)π/b(a − x))]
π n=0 sinh((2n + 1)πa/b)
2
(8)
(a) usando (7) com a = 2.5 e b = 1
(b) usando (8) com a = 5, b = 1
Figura 3: Resposta exercı́cio 1
0
a
V
0
Figura 4: Retângulo semi-infinito
2. Considere a configuração de um retângulo semi-infinito mostrado na Fig. 4. Obtenha a expressão do potencial
dentro do retângulo e plote o resultado, considere a = 1 cm
resposta:
2V
arctan
φ(x, y) =
π
sin(πy/a)
sinh(πx/a)
(9)
A Fig. 5 apresenta o gráfico da solução apresentada em (9). É possı́vel também obter a resposta para esse
problema fazendo b → ∞ em (7).
Figura 5: Resposta exercı́cio 2
3. Calcule o potencial para as configurações de eletrodos mostrados na Fig. 6. Calcule o potencial na região interna
delimitada pelos eletrodos.
3
(a) Eletrodo finito
(b) Eletrodo infinito – o potencial é nulo para
y = ±b e x > a
Figura 6: Eletrodos retangulares
resposta: (a)
ϕ(x, y) = V
∞
2 X cosh(nπy/a) sin(nπx/a)
x/a +
π n=1 cosh(nπb/a)
n
!
(10)
A solução é visualizada na Fig. 7 a seguir. Devido a simetria do problema é possı́vel obter a solução resolvendo
a equação de Laplace em apenas um dos eletrodos, i.e., utilizando apenas três condições de fronteira.
Figura 7: Resposta exercı́cio 3(a)
solução parcial: (b) Como nos casos anteriores trata-se da resolução da equação de Laplace em coordenadas
cartesianas onde o potencial possui as seguintes condições de contorno
ϕ|x=0 = V
ϕ|y=±b = f (x)
onde f (x) = V para 0 ≤ x < a e f (x) = 0 caso contrário. Dessa forma a solução é do tipo
∞
2n + 1
2X
φ̄ cos
πy
ϕ(x, y) =
b n=0
2b
(11)
(12)
onde
Z
b
ϕ(x, y) cos
φ̄ =
0
2n + 1
πy dy
2b
(13)
o processo para determinar as funções desconhecidas φ̄ é o mesmo da determinação de coeficientes da série de
Fourier. Após a determinação desse coeficientes a aplicação direta dos mesmo resulta em

h
i
∞
P
cos((2n+1)πy/(2b))

(−1)n + (−1)n+1 exp (−(2n + 1)πa/(2b)) sinh (2n+1)πx
x<a
 4V
π
2n+1
2a
n=0
φ(x, y) =
(14)
∞
P
(−1)n
(2n+1)πa
(2n+1)πy

 4V
cosh
exp
(−(2n
+
1)πx/(2b))
cos
x
>
a
π
2n+1
2b
2b
n=0
4. Uma linha de carga com carga q por unidade de comprimento é colocada dentro de uma caixa metálica cuja
seção reta é definida pelo “retângulo curvilı́neo” a ≤ r ≤ b, 0 ≤ θ ≤ α. Calcule o potencial u(r, θ) dentro da
caixa.
4
resposta: para r ≤ r0
u(r, θ) = 4q
∞
X
n=1
b
r0
nπ/α
b nπ/α
a
−
r0 nπ/α
b
−
a nπ/α
b
0
sin nπφ
r nπ/α a nπ/α
nπθ
α
−
sin
n
a
r
α
(15)
" #
nπ/α
r nπ/α
b
nπθ
−
sin
r
b
α
(16)
para r ≥ r0
u(r, θ) = 4q
∞
X
r0 nπ/α
a
−
n=1
b nπ/α
a
−
a
r0
nπ/α
a nπ/α
b
0
sin nπφ
α
n
onde r0 e φ0 são as coordenadas polares da linha de carga.
5. Considere um cilindro condutor infinito segmentado de forma que cada um dos hemisférios da seção circular
estão em potenciais distintos, conforme mostra a Fig. 8. Calcule o potencial no interior do cilindro. O raio da
seção circular é de a = 1 m. Considere que o gap que separa os hemisférios é infinitesimal e possui um material
isolante capaz de suportar o gradiente de tensão.
Figura 8: Cilindro segmentado
resposta:
ϕ(r, φ) =
V
2
1+
2
arctan
π
2 ar cos φ
a2 − r2
(17)
6. Um eletrodo retangular possui um seção transversal definida por um retângulo de largura a e altura b e profundidade h. Supondo que uma corrente I é injetada e drenada do eletrodo, conforme mostra a Fig. 9, calcule a
distribuição de potencial no interior do eletrodo. Suponho que o eletrodo é isotrópico e uniforme com condutância
σ.
Figura 9: Eletrodo retangular
resposta:
"
#
∞
I
x
2 X sinh(nπx/b)
φ(x, y) = −
+
cos(nπy/b)
2σh b
π n=1 n cosh(nπa/b)
(18)
solução: Para resolver o problema é necessário supor que a corrente se distribui uniformemente com densidade
I/(2h) numa pequena seção |y| < . Com isso o problema passa a ser a resolução da equação de Laplace em
coordenadas cartesianas
∂2φ ∂2φ
+ 2 =0
∂x2
∂y
5
(19)
com as condições de contorno
∂φ =0
∂y y=±b
∂φ = 0 se |y| > ∂x x=±a
∂φ = −J/(2σh) se |y| < ∂x x=±a
(20)
Utilizando a expansão em série de Fourier do potencial leva a
φ = c0 x +
∞
X
cn sinh (nπx/b) cos(nπy/b)
(21)
n=1
logo
1
c0 =
b
Z
b
I/(2σh)dy
0
2
cn =
nπ cosh(nπa/b)
(22)
b
Z
I/(2σh) cos(nπy/b)dy
0
para n = 1, 2, . . . e calculando o limite quando → 0 obtemos os coeficientes para representar (18).
7. Uma reta de carga com densidade linear q é colocada dentro de um cilindro condutor de raio a, conforme
mostrado na Fig. 10. Suponha que o cilindro é mantido aterrado. Utilize o método das imagens e obtenha a
expressão do potencial dentro do cilindro. Suponha agora que a carga é colocada no lado de fora do cilindro, i.e.
b > a, suponha nesse caso que o cilindro possui uma carga Q por unidade de comprimento e calcule o potencial
no exterior ao cilindro.
bi
a
r
R
Ri
φ
q
b
Figura 10: Cilindro condutor e reta de carga
solução (a): O potencial na superfı́cie do cilindro é nulo, deve haver um potencial u que anule o efeito do
potencial devido à linha de carga. Logo, a expresssão do potencial utilizando coordenadas polares (r, φ) e
normalizando em relação o termo 2π é dado por
ϕ(r, φ) = q ln R + u
p
onde R = r2 + b2 − 2br cos φ . As condições de fronteira implicam que
p
u(r = a) = −q ln a2 + b2 − 2ab cos φ
que no caso de uma ponto genérico pode ser escrito como
 s

2
a br
br 
u = −q ln a 1 − 2
cos φ +
= −q ln
Ri
2
2
a
a
b
onde Ri =
p
r2 + b2i − 2bi r cos φ e bi = a2 /b. Aplicando (25) em (23) e rearranjando os termos leva a
R
b
ϕ(r, φ) = q ln
+ ln
Ri
a
(23)
(24)
(25)
(26)
Por que esse resultado parece diferente daquele obtido utilizando coordenadas cartesianas e mostrado abaixo?
q
(x − b)2 + y 2
q
R
ϕ(x, y) = ln
= ln
(27)
2
2
2
(x − bi ) + y
2 Ri
resposta (b):
ϕ(r, φ) = q ln
onde as distâncias são mostradas na figura abaixo.
6
R
+ (q + Q) ln r
Ri
(28)
Figura 11: Imagem de uma linha de carga dentro de um cilindro condutor
8. Considere uma carga pontual q colocada entre dois planos condutores infinitos. O primeiro é colocado em y = 0
e o segundo em y = d, as coordenadas da carga são x0 e y0 , vide Fig. 12. Calcule o potencial na região definida
entre os dois planos. O que mudaria nos resultado se ao invés de dois planos houvesse duas linhas condutoras e
a carga fosse pontual?
Figura 12: Múltiplas imagens
resposta:
φ(x, y) =
n=+∞
(x − x0 )2 + (y + y0 + 2nd)2
1 X
ln
2 n=−∞
(x − x0 )2 + (y − y0 + 2nd)2
(29)
onde x0 e y0 representada as coordenadas da carga pontual e d a separação entre os planos.
9. Um tubo definido por a ≤ r ≤ b feito por um material de permeabilidade relativa µr = 5 é colocada em campo
magnético constante H0 . Calcule a distribuição de potencial magnético e plote o resultado suponha b/a = 1, 5.
solução: O potencial escalar aqui é chamado de u para evitar possı́veis confusões com a coordenada φ. O
problema se reduz a integração de um sistema de equações diferenciais dado por
1 ∂ r∂ui
1 ∂ 2 ui
+ 2
(30)
r ∂r
∂r
r ∂φ2
onde os potenciais ui são definidos por
b < r < ∞,
i=1
a < r < b,
i = 2, π < φ ≤ π
0 < r < a.
i=3
(31)
e as condições de contorno são dadas por
u1 (r → ∞) → H0 x
∂u1 ∂u2 =
∂φ r=b
∂φ r=b
∂u1 ∂u2 =µ
∂r r=b
∂r r=b
∂u2 ∂u3 =
∂φ r=a
∂φ r=a
∂u2 ∂u3 µ
=µ
∂r r=a
∂r r=a
(32)
Levando-se em conta que devido a simetria do problema só haverá funções pares as seguintes funções podem ser
7
usadas para representar os potenciais ui
u1 = H0 r cos φ +
∞
X
An r−n cos(nφ)
n=1
u2 = C0 ln r +
∞
X
Bn rn + Cn r−n cos(nφ)
(33)
n=1
u3 =
∞
X
Dn rn cos(nφ)
n=1
Devido às condições de contorno as contantes C0 e Cn para n ≤ 2 devem ser nulas. Para determinar as outras
contantes basta aplicar (33) em (32). Isso leva ao sistema de equações
A1 − b2 B1 − C1 = −H0 b2
A1 + µb2 B1 − µC1 = H0 b2
(34)
a2 B1 + C1 − a2 D1 = 0
µa2 B1 − µC1 − a2 D1 = 0
o que leva a
H0 b2 (µ2 − 1)(b2 − a2 )
b2 (µ + 1)2 − a2 (µ − 1)2
2H0 b2 (µ + 1)
B1 = 2
b (µ + 1)2 − a2 (µ − 1)2
2H0 a2 b2 (µ − 1)
C1 = 2
b (µ + 1)2 − a2 (µ − 1)2
4H0 b2 µ
D1 = 2
b (µ + 1)2 − a2 (µ − 1)2
A1 = −
A aplicação de (35) em (33) leva a solução do problema, conforme mostrado
h
i

(µ2 −1)(b2 −a2 )
2

H0 r cos φ 1 − b2 (µ+1)
2 −a2 (µ−1)2 (b/r)


2
2
)
u(r, φ) = H0 r cos φ 2b (2(1+µ)+(µ−1)(a/r)
b (µ+1)2 −a2 (µ−1)2


2

H0 r cos φ b2 (µ+1)4µb
2 −a2 (µ−1)2
(35)
abaixo.
b≤r<∞
a≤r≤b
(36)
0≤r<a
A Fig. 13 mostra a visualização das linhas de força. O processo para obter as linhas é o seguinte: calcule
H = ∇u(rφ) e obtenha o vetor densidade de campo magnético B. Calcule o fluxo de B e através dos tubos de
fluxo obtenha as linhas de força.
Figura 13: Cilindro oco imerso em campo magnético
8
10. Uma esfera oca dada por a ≤ r ≤ b é imersa em um campo magnético Hz = −H0 . Calcule o potencial magnético
e plote o resultado, suponha a mesma permeabilidade relativa do caso anterior e a = 3 cm e b = 5 cm.
resposta:

9b3 µH0 r cos θ

3 (µ+2)(2µ+1)−2 a3 (µ−1)2
b


3(b/r)3 H0 r cos θ [r 3 (2µ+1)+a3 (µ−1)]
ϕ(r, θ) =
b3 (µ+2)(2µ+1)−2 a3 (µ−1)2


(b/r)3 H0 r cos θ [(a3 −b3 )(µ−1)(2µ+1)]

H0 r cos θ +
b3 (µ+2)(2µ+1)−2 a3 (µ−1)2
0≤r≤a
a<r≤b
(37)
b<r<∞
A solução desse problema pode ser encontrado no livro “Classical Electrodynamics,” J. D. Jackson, 3rd Ed.,
Wiley. A Fig. 14 a seguir mostra o comportamento do campo magnético. As rotinas utilizadas no gráfico foram
obtidas de:
"Spherical Shell in a Magnetic Field" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/SphericalShellInAMagneticField/
Compare o resultado desse exercı́cio com o anterior. O que muda de uma configuração para outra? Poderia ser
utilizado o mesmo caso para a representação das duas configurações?
Figura 14: Casca esférica em campo magnético uniforme
11. Mostre que o potencial eletrostático em coordenadas polares dentro de uma esfera de raio a se um hemisfério é
mantindo no potencial V , i.e.
ϕ(r, θ) = V
0 ≤ θ ≤ π/2
enquanto o outro hemisfério está aterrado é dado por
"
#
∞
X
4n + 3
V
2n+1
ϕ(r, θ) =
1+
P2n (0) (r/a)
P2n+1 (cos θ)
a
2n + 2
n=0
solução: Da solução da equação de Laplace em coordenadas esféricas temos que as soluções são do tipo
∞ X
Bk
k
ϕ(r, θ) =
Ak r + k Pk (cos θ)
r
(38)
(39)
(40)
k=0
Como estamo interessados no potencial no interior da esfera Bk = 0. A condição de contorno especifica o
potencial na superfı́cie da esfera, i.e. para r = a o potencial é dado por (38). Logo, (40) pode ser vista como uma
expansão em série de Fourier do potencial na superfı́cie da esfera. Uma vez que esse potencial é para 0 ≤ θ < π/2
temos
Z 2π Z π/2
1
Ak = k
Pk (cos θ) sin θ dφ dθ
(41)
a 0
0
9
para k impar. Do cálculo sabemos que
Z
Pk−1 (cos θ) − Pk+1 (cos θ)
Pk (cos θ) sin θ dθ =
2k + 1
(42)
Aplicando os limites a (42) e após alguma manipulação algébrica otemos a expressão em (39). A Fig. 15(a)
apresenta o gráfico de ϕ(r, θ) para r = a e a Fig. 15(b) traz o gráfico da mesma função para 0 ≤ r ≤ 1 e
0 ≤ θ < π/2.
(a)
(b)
Figura 15: Gráficos para a resposta (39)
Esse problema também pode ser resolvido utilizando a função associada de Legendre cuja a definição é dada por
(43).
Pkm (x) = (−1)m (1 − x2 )m/2
dm Pk (x)
dxm
(43)
Nesse caso as soluções são dadas por
ϕ(r, θ, φ) =
∞ X
k
X
Akm
exp(jmφ)Pkm (cos θ)
rk+1
(44)
k=0 m=−k
Em diversas configurações é interessante combinar as funções de Legendre e a exponencial em φ. Esse tipo de
função é também conhecido como harmônico esférico cuja definição é mostrada em (45).
s
2k + 1 (k − m)! m
P (cos θ) exp(jmφ)
(45)
Yk,m (θ, φ) =
4π (k + m)! k
Para o problema em questão há simetria em relação ao eixo φ, com isso m = 0. As funções a serem utilizadas
na solução são mostradas em (46).
∞
X
Ãk rk Yk,0 (θ, φ)
(46)
√ √
a−k π 1 + 2k 1
Yk,0 (θ, φ) sin θ dθ = −
Pk (0)
k(k + 1)
(47)
ϕ(r, θ, φ) =
k=0
Os coeficientes são dados por
2π
Ãk = k
a
Z
0
π/2
A Fig. 16 sendo possı́vel notar que as formas são essencialmente iguais a diferença fica apenas na escala do
potencial que no caso de harmônicos esféricos é normalizada.
10
Figura 16: Potencial dentro da esfera obtido utilizando harmônicos esféricos
Figura 17: Disco condutor e carga pontual
12. Utilizando o método dos momentos calcule a densidade de carga σ em um disco condutor de raio a devido a uma
carga pontual q a uma distância ` do eixo de simetria do disco, vide Fig. 17.
resposta:
#
"
∞
X
−3/2
q
j2
2
n (4n + 1)n!
2
2
σ=−
(a/`) 1 + (a/`) sin β
+√
(−1)
Q2n (j`/a)P2n cos β
4πa2
Γ(n + 1/2)
π cos β n=0
(48)
onde β = arcsin(r/a), onde r é a distância de um ponto numa posição arbitrária na superfı́cie do disco ao centro
do mesmo, Qn (.) é a função de Legendre de segunda espécie, vide
http://mathworld.wolfram.com/LegendreFunctionoftheSecondKind.html
Esse problema também pode ser resolvido utilizando diretamente equações integrais, vide Weisstein, Eric W.
”Integral Equation.”From MathWorld–A Wolfram Web Resource, cuja url é:
http://mathworld.wolfram.com/IntegralEquation.html
Isso leva a seguinte expressão para a densidade de carga na superfı́cie mais próxima da carga pontual
"
! r
#
r
q` 2
a2 − r2
`2 + r2
π
2 −3/2
σ(r) = − 2 ` + r
arctan
+
±
2π
`2 + r2
a2 − r2
2
11
(49)
dica: O problema deve ser resolvido considerando que o potencial num ponto arbitrário distando R da carga
pontual é dado por
q
+ u1
(50)
ϕ=
R
e o potencial deve atender à equação de Laplace
∇2 ϕ = 0
(51)
otendo a expressão do potencial a densidade de carga pode ser obtida pela derivada do potencial.
2
Propagação de Ondas
1. Uma onda plana possui apenas componente z dada por
Ez = E0 exp (jω t − jkz)
(52)
onde k = ω/c. Essa onda incide num cilindro condutor perfeito de raio a. Mostre que o campo difratado é dado
por
"
#
∞
X
J0 (ka)
J
(ka)
n
(2)
Ez = E0 exp(jω t) exp(−jkr cos φ) − (2)
H0 (kr) − 2
Hn(2) (kr) cos(nϕ)
(53)
(−j)n (2)
H0 (ka)
H
(ka)
n
n=1
solução: Esse exercı́cio consiste em achar a amplitude da onda de campo elétrico que satifaz a equação de onda
∂E
1 ∂2E
1 ∂
r
+ 2
+ k2 E = 0
(54)
r ∂r
∂r
r ∂φ2
supondo um sistema de coordenadas cilindricas (r, φ, z) e cuja condição de contorno é
Ed + E0 exp(−k a cos φ) = 0
(55)
onde Ed = E(r = a). Como se trata de uma onda temos que o campo deve ser regular no infinito, i.e., E → 0
para r → ∞. Aplicando o método de separação de variáveis a (54) e sabendo que as funções devem ser periódicas
em φ, as soluções são do tipo
En = Mn Hn(1) (kr) + Nn Hn(2) (kr) cos(nφ)
ou
(56)
En = Mn Hn(1) (kr) + Nn Hn(2) (kr) sin(nφ)
(1,2)
onde Hn (.) são funções de Hankel. Devido às condições de simetria do problema o campo elétrico é uma
função par de φ, logo as soluções com sin(nφ) devem ser descartadas. Pela condição de radiação, i.e., funções
(1)
regulares no infinito, as funções de Hankel do tipo Hn (.) devem ser excluı́das o que é possı́vel com Mn = 0.
Logo a solução é do tipo
E=
∞
X
Nn Hn(2) (kr) cos(nφ)
(57)
n=0
pelas condições de contorno
E0 exp(−ka cos φ) +
∞
X
Nn Hn(2) (kr) cos(nφ) = 0
(58)
n=0
e necessário expandir o termo exponencial conforme mostra (59)
exp(−ka cos φ) = J0 (ka) + 2
∞
X
(−j)n Jn (ka) cos(nφ)
(59)
n=1
Aplicando (59) em (58) implica em
(2)
N0 H0 (ka) = −E0 J0 (ka)
Nn Hn(2) (ka) = −2E0 (−j)n Jn (ka)
Logo o campo difratado pelo cilindro é da forma
"
#
∞
X
J0 (ka) (2)
J
(ka)
n
Ed = −E0 exp(jωt)
H0 (kr) + 2
(−j)n
Hn(2) (kr) cos(nφ)
(2)
(2)
H0
H
n
n=1
(60)
(61)
O campo total é dado pela soma do campo incidente com a onda original. A Fig. 18 apresenta uma visualização
do campo total dado por (53).
12
Figura 18: Onda plana difratada de um cilindro condutor ideal, exercı́cio 1
2. Repita o exercı́cio anterior supondo agora que o material do cilindro é isotrópico e uniforme com condutância σ
e permitividade .
p
√
resposta:, para r ≥ a e onde k1 = ω µ e k2 = ω 2 µ − jωµσ
"
k1 J0 (k2 a)J1 (k1 a) − k2 J0 (k1 a) J1 (k2 a)
(2)
Ez = E0 exp(jω t) exp(−jk1 r cos φ) + H0 (k1 r)
(2)
(2)
k2 H0 (k1 a)J1 (k2 a) − k1 J0 (k2 a)H1 (k1 a)
#
(62)
∞
X
k1 Jn (k2 a)Jn+1 (k1 a) − k2 Jn (k1 a) Jn+1 (k2 a)
(2)
exp(−jnπ/2)Hn (k1 r) cos(nφ)
+2
(2)
(2)
k2 Hn (k1 a)Jn+1 (k2 a) − k1 Jn (k2 a)Hn+1 (k1 a)
n=1
3. Seja uma linha de transmissão conforme a fig. 19. A altura dos condutores é considerada constante e o comprimento do circuito pode ser considerada infinito. Os condutores possuem raio r = 10 mm, σ = 30 · 106 S/m e
r − 10 e permeabilidade magnética µ0 . A prı́ncipio considere o solo ideal. Tensões simétricas e equilibradas são
aplicadas nos condutores 1, 2 e 3, onde a tensão e a corrente no condutor 1 são dadas por (63).
u1 = 200 103 cos(2π60 t)
i1 = 500 cos(2π60 t)
(63)
Supondo um condutor isolado cujo ponto P da seção transversal é mostrado na Fig. 19, calcule o campo elétrico
e o campo magnético no no ponto P , ambos em função do tempo. Determine o campo elétrico na superfı́cie do
condutor 1 em função do tempo. Calcule o campo elétrico no solo utilizando os fasores das tensões fase-neutro.
1
2
7
3
P
7
10
5
5
111111111111111111111111
000000000000000000000000
000000000000000000000000
111111111111111111111111
000000000000000000000000
111111111111111111111111
Figura 19: Circuito Simples de Linha de transmissão trifásica
Solução Parcial: Considerando a aproximação quase estacionária a relação entre as cargas de cada condutor e
a tensão transversal dos condutores é do tipo
u = P̂ · q
q =C ·u
(64)
onde u é o vetor das tensões nos condutores e q o vetor de carga em cada um dos condutores. Da expressão em
(64) temos que
P̂ = C −1
13
(65)
A matriz P̂ é do tipo
P̂ =
1
P
2π
(66)
sendo

ln 2h1
 Dr12
P = ln d12
31
ln D
d31
12
ln D
d12
2h1
ln r
32
ln D
d32

12
ln D
d12
23 
ln D
d23 
ln 2hr 3
(67)
onde hi e a altura do condutor i, r o raio do condutor, Dij distância entre o condutor i e a imagem do condutor
j e dij a distância do condutor i ao condutor j. Logo pela relação em (64)
C = 2π P −1
.
(68)
Na literatura técnica tanto P̂ quanto P são conhecidas como a matriz dos coeficientes de potencial de Maxwell.
A formulação utilizada em (67) é um pouco mais eficiente pois evita a utilização da permeabilidade na inversão
da matriz. Evitando-se assim lidar com números muito pequenos. Lembrem que a permeabilidade no ar é 8.8549
10−12 . Aplicando-se os valores numéricos do exercı́cio temos


0.134797
−0.0186005 −0.00715904
0.136984
−0.0186005 
P −1 =  −0.0186005
(69)
−0.00715094 −0.0186005
0.134797
Portanto, seja Ek o campo elétrico na superfı́cie externa do condutor onde Ēkn é o valor médio (ao longo do
perı́metro do condutor) da componente de Ek ortogonal a essa superfı́cie temos os seguintes valores em kV/m


29, 601 cos(ωt + 0.0639877)
1
1
bkn =
q = P −1 u =  31, 117 cos(ωt − 2.09440) 
(70)
E
2π r
r
29, 601 cos(ωt + 2.02735)
Para analisar a variação de Ekn ao longo do perı́metro do condutor vamos decompor a carga qk do condutor k
em cargas qkj sendo j o ı́ndice dos condutores diferentes de k e das imagens desses condutores e do condutor k,
conforme representado esquematicamente na Fig. 20, onde os condutores vermelhos representam as imagens (condutores 4 a 6). As expressões para as cargas por unidade de comprimento nos condutores 1 a 6 são apresentadas
em (71).
Figura 20: Método das imagens para uma LT trifásica



  
Ē1n
q1
q1
 Ē2n 
q2   q2 



  


q3   q3 
 =
 = 2πr  Ē3n 
−Ē1n 
q4  −q1 



  
−Ē2n 
q5  −q2 
q6
−q3
−Ē3n
14
(71)
Como não há outras “fontes” de cargas temos ainda
6
X
qk = 0
(72)
k=1
Consideremos o condutor k e decomponhamos a carga qk em cargas qkj conforme mencionado acima. Consideremos o para de cargas constituı́do pela carga qkj no condutor k e a carga qj no condutor j. Desloquemos a carga
qkj no condutor j de forma que uma equipotencial do campo associado às duas cargas coincida com a superfı́cie
do condutor k.
Consideremos para analisar o campo associado ao par de cargas lineares qkj , qj o sistema apresentada na Fig, 21
onde qkj é designado qi (i.e., carga interna) e a carga qj por qe (carga externa ao condutor). Para esse par
de cargas temos um carga qe , por unidade de comprimento, numa linha de carga paralela ao condutor a uma
distância b desse eixo e a imagem dessa carga em relação à superfı́cie cilı́ndrica do condutor constituı́da por uma
linha de carga a uma distância a do eixo com carga por unidade de comprimento qi = −qe tal que o conjunto
das duas cargas lineares origina um campo em que uma equipotencial coincide com a superfı́cie do condutor.
Sabemos também que ab = r2 , vide exercı́cio 7.
Figura 21: Par de cargas (interna e externa) associada ao condutor
O potencial ϕ(x, y) associado ao par de carga lineares [qi = −qe , qe ] é dador por
ϕ(x, y) =
qi
(x − b)2 + y 2
ln
4π (x − a)2 + y 2
e o campo elétrico no ar é dado por
qi
x−a
y
x−b
y
E = −∇ϕ(x, y) =
+
x̂ +
−
ŷ
2π
(x − a)2 + y 2
(x − a)2 + y 2
(x − a)2 + y 2
(x − b)2 + y 2
(73)
(74)
Consideremos um ponto genérico na superfı́cie do condutor, definido pelo ângulo α conforme apresentado na
Fig. 21, nesse caso o campo elétrico é obtido considerando x = r cos α e y = r sin α em xs(74).
A componente do campo elétrico ortogonal à superfı́cie do condutor, En é dada por (75), lembremos que a = r2 /b
En = Ex cos α + Ey sin α
qi
r − b cos α
r − a cos α
=−
−
2π (r cos α − b)2 + (r sin α)2
(r cos α − a)2 + (r sin α)2
qi
r − b cos α
r − (r2 /b) cos α
=−
−
2π r2 − 2rb cos α + b2
r2 − 2r3 /b cos α + (r2 /b)2
qi
1
r
1
1 1
=−
−
cos
α
−
+
cos
α
2π 1 − 2r/b cos α + (r/b)2 b2
b
r
b
qi
1 − (r/b)2
=
2π r 1 − 2r/b cos α + (r/b)2
Supondo r/b 1 o campo pode ser expresso por (76).
qi
2r
En ≈
1+
cos α
2π
b
(75)
(76)
Vamos supor agora que a carga qe é colinear mas agora faz um ângulo φ em relação ao eixo utilizado anteriormente.
Supondo ainda que r/b 1 o campo pode ser representado por
qi
2r
En ≈
1+
cos(α − φ)
(77)
2π
b
15
Logo para o conjunto de pares de cargas k, j que definem o campo na vizinhança externa ao condutor k temos
6
X
r
qkj
Ekn ≈
1+2
cos (α − φkj )
(78)
2π r
bkj
j=1,j6=k
Para k = 1 temos
T
√
√
b1j = 7 14 20
449
596
T
φ1j = 0 0 − π2 − arctan(20/7) − arctan(20/14)
T qkj = q12 q13 q14 q15 q16 = −q2 −q3 −q4 −q5
(79)
−q6
T
O campo elétrico para o primeiro condutor k = 1 é dado por (80) em kV/m onde θ = ωt. Da expressão
mencionada podemos notar que há diversas parcelas no campo elétrico. Para um dado instante de tempo, há
uma parcela constante e outras duas função de α−θ e α+θ. Essas duas últimas parcelas correspondem a campos
girantes um no sentido de α crescente e outro no sentido contrário.
E1n ≈ 2960, 1 cos(θ − 0, 06705) + 3, 33 cos(α − θ + 0, 84998) + 3, 52 cos(α + θ + 0, 5409)
(80)
A Fig. 22 apresenta diversas curvas de nı́vel para o campo elétrico na superfı́cie do condutor para diferentes
valores de θ próximas ao máximo do campo elétrico em função de α. O campo elétrico máximo para o condutor
1 ocorre quando θ = 0, 06705 + 2πn, onde n é um número inteiro. A Fig. 23 apresenta E1n correspondente ao
campo elétrico na superfı́ce do condutor para θ = 0, 06705 + 2π.
Figura 22: Curvas de nı́vel do campo elétrico na superfı́cie do condutor 1
Da expressão (80) vemos que a amplitude da parcela correspodente ao valor médio é muito superior às parcelas
devidas aos campos girantes. O o valor máximo de E1n é muito próximo à soma dos valores máximo de cada
parcela. Em outras palavras, E1n é máximo para θ = 0, 06705+2πn e α = 0 que corresponde a aproximadamente
2965,35 kV/m.
A componente do campo elétrico tangencial à superfı́cie dos condutores é devida à variação temporal do vetor
potencial, em outras palavras
E = −∇ϕ(x, y) −
16
∂A(x, y, t)
∂t
(81)
Figura 23: Campo elétrico na superfı́cie do condutor 1
Nas condições do problema, i.e., com distâncias entre condutores e condutores e solo muito superiores ao raio
dos condutores, a componente tangencial do campo elétrico tangencial à superfı́cie dos condutores, Ekt , é aproximadamente paralela ao eixo dos condutores. Considerando variações temporais dadas por funções harmônicas,
i.e exp(jωt) e supondo que nos condutores σ ω temos
Ekt = <(Ekt exp(jωt))
(82)
onde Ekt = Zin Ik , sendo Zin a impedância interna por unidade de comprimento e Ik a corrente que percorre o
condutor k. No caso de condutores cilı́ndricos sólidos de raio r temos
r
√
1
jωµ I0 r jωµσ
Zin =
(83)
√
2πr
σ I1 r jωµσ
sendo σ a condutividade do condutor e µ a permeabilidade magnética do mesmo.Para as condições do enuciado,
i.e., correntes simétricas e equilibradas e com valores de pico iguais a 500 A temos os valores para o campo
elétrico tangencial em V/m apresentados em (84).
T
Ekt = 10−3 54, 42 cos(θ + 0, 17315) 54, 42 cos(θ − 1, 92124) 54, 42 cos(θ + 2, 26754)
(84)
Vejamos agora o campo elétrico no ponto P (não há relação entre esse ponto e a matriz de coeficientes de Maxwell
e só que as vezes faltam letras para o estudo do eletromagnetismo). Consideremos regime quase-estacionário
e para efeito da componente do campo elétrico no ar transversal à direção dos condutores, o solo se comporta
como um meio de condutividade infinita. Essa restrição pode ser expressa também pela seguinte relação
|σs + jωs | |jω|
onde o indı́ce s indica os parâmetros do solo e é a permitividade do ar.
Nessas condições o campo elétrico no ar pode ser obtido utilizando-se o método das imagens. O campo elétrico
no ponto P no ar correspondente às cargas nos condutores e às respectivas imagens é dado por
6
1 X
xp − xk
yp − yk
E = −∇ϕ =
qk
x̂
+
ŷ
(85)
2π
(xp − xk )2 + (yp − yk )2
(xp − xk )2 + (yp − yk )2
k=1
sendo (xp , yp ) as coordenadas do ponto P , (xk .yk ) as coordenadas dos condutores e das respectivas imagens, e
qk as cargas por unidade de comprimento dos condutores e das respectivas imagens. Aplicando-se os dados do
enunciado obtemos o campo elétrico em kV/m conforme (86).
E = 1, 14409 cos(ωt − 3.8664) x̂ + 3, 15265 cos(ωt − 0.849943) ŷ
(86)
A Fig. 24 apresenta o comportamento do campo elétrico no ponto P em função das componentes Ex e Ey . Já o
módulo do campo elétrico varia no espaço no ponto P conforme mostra a Fig. 25. O módulo do campo elétrico
é obtido por
q
|E| = Ex2 + Ey2
(87)
17
Figura 24: Extremidade do vetor de campo elétrico no ponto P em função do tempo
e o valor médio, no tempo do módulo (no espaço) do campo elétrico em kV/m é apresentando em (88).
Z 2π q
1
E=
Ex2 + Ey2 dθ = 2, 14043
2π 0
(88)
Figura 25: Variação temporal do módulo do campo elétrico no ponto P
Conforme mencionado anteriormente, a componente z do campo elétrico, Ez paralela ao eixo dos condutores
está basicamente associada a -∂A/∂t. Em função das hipótese indicadas e por tratar-se de um regime de carga
da linha com valor nulo da soma das correntes nos condutores 1, 2, 3, sendo portanto reduzidas as correntes no
solo, Ez tem amplitude muito inferior à amplitude de Et com ordem de grandeza igual ou inferior à ordem de
grandeza da componente z do campo elétrico na superfı́cie dos condutores. Fazendo-se o ponto P ficar na altura
do solo, i.e. (xp = x, yp = 0), obtemos a expressão do campo elétrico no solo em função da coordenada x. A
Fig.26 apresenta o comportamento do valor eficaz do campo elétrico no solo para a configuração em questão.
Para o caso do campo magnético vamos supor, a prı́ncipio, que o solo se comporta como um meio de condutividade
infinita. Nessas caso, o campo magnético no solo é nulo. Como ∇ · B = 0 e supondo que a permeabilidade
18
Figura 26: Campo Elétrico no solo (valor eficaz)
magnética relativa no ar e no solo é idêntica, a componente de H ortogonal à superfı́cie que separa o solo e
o ar é contı́nua ao atravessar a separação entre os meios. Portanto, na vizinhança que separa os meios H é
tangencial à superfı́cie que separa os meios. Nessas condições e nas hipóteses do problema, a componente de
Ht do campo magnético no transversal à direção dos condutores pode ser obtida utilizando-se o método das
imagens. Passamos então a ter seis correntes sendo i4 = −i1 , i5 = −i2 e i6 = −i3 . O campo magnético num
ponto P é dada por
Ht =
6
X
ik
xp − xk
yp − yk
x̂
+
ŷ
−
2π
(xp − xk )2 + (yp − yk )2
(xp − xk )2 + (yp − yk )2
(89)
k=1
sendo xp , yk , xk , yk os mesmos no caso do campo elétrico e ik a corrente no condutor k. Aplicando-se as
condições dadas no problema obtemos a seguinte expressão para o campo magnético em A/m
Ht = 56, 72 cos(ωt + 2, 483) x̂ + 10, 79 cos(ωt + 2, 74) ŷ
(90)
A Fig. 27 apresenta a variação das componentes x e y do vetor tangencial do campo magnético no ponto P .
H=
1
2π
Z
2π
q
Hx2 + Hy2 dθ = 36, 9185
(91)
0
O modulo do campo magnético no espaço no ponto P varia no tempo conforme apresentado na Fig. 28. O valor
quadrático médio, no tempo, do módulo, no espaço de Ht é dado por (91) em A/m.
4. Repitir o procedimento do exercı́cio anterior para as linhas de transmissão onde as coordenadas dos condutores
são
• Circuito de 345 kV convencional
−7.229 10.5
−6.771 10.5
−0.229 10.5
0.229 10.5
7.229 10.5
6.771 10.5
19
(92)
Figura 27: Extremidade do vetor de campo magnético no ponto P em função do tempo
Figura 28: Variação temporal do módulo do campo magnético no ponto P
• Circuito convencional de 500 kV
−7.229
−7.229
−6.771
−6.771
−0.229
−0.229
0.229
0.229
7.229
7.229
6.771
6.771
20
8.639
10.5
10.5
8.639
10.5
9.876
9.876
10.5
8.639
10.5
10.5
8.639
(93)
• Circuito compacto de 500 kV
−4.271
−4.271
−4.729
−4.729
0.229
0.229
−0.229
−0.229
4.271
4.271
4.729
4.729
10.771
11.229
11.229
10.771
15.271
15.729
15.729
15.271
10.771
11.229
11.229
10.771
(94)
−7.229
−7.229
−6.771
−6.771
−0.229
−0.229
0.229
0.229
7.229
7.229
6.771
6.771
8.639
10.5
10.5
8.639
10.5
9.876
9.876
10.5
8.639
10.5
10.5
8.639
(95)
• Circuito não convencional de 500 kV
5. Considere um condutor vertical de aço,”muito longo” não isolado, imerso no solo, suposto homogêneo e isotrópico.
Suponha uma corrente senoidal injetada na interface solo-ar de valor eficaz igual a 100 A, 1 kHz. Determine o
valor da corrente (amplitude e fase) no condutor em função da profundidade até 100 m abaixo da superfı́cie do
solo. Considere coordenadas cilindricas z, r, θ, onde z = 0 corresponde a superfı́cie do solo e z > 0 no solo. Os
dados são:
Condutor σ = 3 · 106 S/m, r = 10, µr = 1, r = 5 cm
Solo σ = 0.01 S/m, r = 100, µr = 1
extra Reproduzir os resultados referentes à constante de propagação para um condutor de comprimento infinito sobre
um solo não ideal apresentados no artigo: “Simulation Models of a Dissipative Transmission Line Above a Lossy
Ground for a Wide-Frequency Range—Part I: Single Conductor Configuration,” IEEE Trans. on Electromagnetic
Compatibility, Vol. 38, No. 2, May 1996.
21