Texto Completo - FAMAT

SERVIÇO PÚBLICO FEDERAL
UNIVERSIDADE FEDERAL DO SUL E SUDESTE DO PARÁ
INSTITUTO DE CIÊNCIAS EXATAS
FACULDADE DE MATEMÁTICA
CURSO DE LICENCIATURA PLENA EM MATEMÁTICA
JOSÉ RICARDO DOS SANTOS FREITAS
ASPECTOS GERAIS DA SÉRIE DE FOURIER
Marabá – PA
FAMAT - UNIFESSPA
2016
SERVIÇO PÚBLICO FEDERAL
UNIVERSIDADE FEDERAL DO SUL E SUDESTE DO PARÁ
INSTITUTO DE CIÊNCIAS EXATAS
FACULDADE DE MATEMÁTICA
CURSO DE LICENCIATURA PLENA EM MATEMÁTICA
JOSÉ RICARDO SANTOS FREITAS
ASPECTOS GERAIS DA SÉRIE DE FOURIER
Trabalho de Conclusão de Curso apresentado à
Universidade Federal do Sul e Sudeste do Estado do
Pará como requisito para obtenção do título em
Licenciatura Plena em Matemática.
Área de Concentração: Matemática e Programação.
Orientador: Prof. Msc. Pedro Cruz Nunes de Moraes
Marabá – PA
FAMAT - UNIFESSPA
2016
Dados Internacionais de Catalogação-na-Publicação (CIP)
Biblioteca II da UNIFESSPA. CAMAR, Marabá, PA
Freitas, José Ricardo Santos
Aspectos Gerais da série de Fourier / José Ricardo Santos Freitas;
orientador, Pedro Cruz Nunes de Moraes. — 2016.
Trabalho de Conclusão de Curso (Graduação) - Universidade Federal do
Sul e Sudeste do Pará, Campus Universitário de Marabá, Instituto de Ciências
Exatas, Faculdade de Matemática, Curso de Licenciatura Plena em
Matemática, Marabá, 2016.
1. Matemática Aplicada. 2. Série de Fourier (Matemática). 3. MATLAB
(Programa de computador). I. Moraes, Pedro Cruz Nunes de, orient. II.
Título.
CDD: 22. ed.: 519.4
SERVIÇO PÚBLICO FEDERAL
UNIVERSIDADE FEDERAL DO SUL E SUDESTE DO PARÁ
INSTITUTO DE CIÊNCIAS EXATAS
FACULDADE DE MATEMÁTICA
CURSO DE LICENCIATURA PLENA EM MATEMÁTICA
JOSÉ RICARDO SANTOS FREITAS
Trabalho de Conclusão de Curso apresentado à
Universidade Federal do Sul e Sudeste do Estado do Pará
como requisito para obtenção do título em Licenciatura
Plena em Matemática.
Área de Concentração: Matemática e Programação.
Orientador:Prof. Msc. Pedro Cruz Nunes de Moraes
DATA DA DEFESA: __/___/______
CONCEITO:_______________
BANCA EXAMINADORA
_______________________________________________
Prof. Eng. Ms.C. Pedro Cruz Nunes de Moraes
Orientador
_______________________________________________
Prof. Eng. Esp. Geraldo Lopes Daltro da Silveira
Membro 1 – FACULDADE METROPOLITANA – MARABÁ
________________________________________________
Prof. Ms.C. Claudionei Pereira de Oliveira
Membro 2 – UNIFESSPA
________________________________________________
Prof. Ms.C. Clayton Douglas Chagas de Oliveira
Suplente - UNIFESSPA
Os SÁBIOS perdoam, mas
nem sempre TOLERAM.
Pcruz
DEDICATÓRIA
Dedico este trabalho a minha
Família, que sempre me deu forças
em todos os momentos e a meus pais,
José Costa Freitas e Raimundinha
Alves dos Santos.
AGRADECIMENTOS
Agradeço antes de tudo ao Senhor meu Deus que me concedeu o dom da vida,
sempre está comigo me guiando e me ajudando a tomar as melhores decisões, me tratando
com misericórdia em todos os momentos difíceis. Agradeço a minha família, por ter
sempre me incentivado e nunca ter medido esforços para me ajudar em todos os percalços
ao longo desta empreitada. Agradeço especialmente a meu irmão Elken Freitas por ser uma
pessoa em quem eu posso me espelhar e seguir suas atitudes.
Agradeço a meu pai José Costa Freitas que me ensinou a trabalhar e nunca trilhar
por caminhos errados. Minha mãe Raimundinha Alves dos Santos que sempre foi a grande
responsável por me comprometer com a educação e nunca desistir frente aos problemas
que pudessem surgir, sempre intercedendo junto a Deus a meu favor.
Agradeço a meu Orientador e amigo Pedro Cruz, que viu em mim algo em
potencial e tem me ensinado a fazer um bom trabalho, qualquer que seja a vertente, um
grande amigo que me ensina a superar as dificuldades com sabedoria e humildade.
Reconheço a ajuda dos meus amigos que me auxiliaram concluir e tolerar os
problemas que por ventura aconteceram em especial meus amigos Mathias Formachare,
Bento Cleiton de Oliveira e família e Prefeito Ruan. E não menos, importante gostaria de
agradecer aos meus amigos que em muitos momentos estivemos juntos enfrentando as
diversidades; Diego Pantoja, Anderson Penalva, Irmão Valdivino, Benedito Sousa
juntamente com o Projeto Educando Para Viver, minha amiga Sâmila Lavyni. Agradeço a
Sara Mileide pela paciência e incentivo. Não posso deixar de agradecer a minha turma de
fato 2011 e a todos os meus colegas da turma de direito 2012 que ao longo desse percurso
tem convivido, a Professora Renata Laurinho, muito obrigado. Agradeço ainda à Ana Tigre
pela força que está me dando nesse momento. Mais uma vez gostaria de agradecer ao
Math-Up e a Deus por tudo, por todos que entraram em meu caminho e que continuem
surgindo pessoas boas no meu trajeto acadêmico.
RESUMO
Esta monografia começa com as definições de funções periódicas, ciclo
trigonométrico, seno, cosseno, tangente, função par e ímpar e suas respectivas proposições
com as demonstrações correspondentes. Abrindo um leque para as integrais de funções
pares e impares. Em seguida têm-se o cuidado de definir a frequência, período e
caracterizar a diferença entre frequência e frequência angular para introduzi-las nas séries
trigonométricas. Faz-se um breve histórico de como Fourier chegou as deduções dos
coeficientes da sua série escrevendo em seu livro intitulado “Teoria Matemática da
Condução de Calor”, destacando matemáticos que trabalharam essa mesma ideia, como:
Euler, Bernoulli, Taylor, Maclaurin entre outros. A seguir faz-se uma exposição de funções
ortogonais, mostrando um sistema ortonormado e deduzindo por meio desses conceitos, os
coeficientes de Fourier, de maneira análoga usando as identidades trigonométricas para
resolver algumas integrais peculiares ao tema, com a representação do Delta de Kronecker
se encontra os mesmos resultados para os coeficientes de Fourier. Depois da definição de
função seccionalmente contínua por partes é discutido os problemas de funções suaves,
muito suaves, saltos e cantos. Procurando sempre demonstrar todos os teoremas e
corolários que contenham funções contínuas inclusive a própria série. Aplicando essa
teoria em algumas funções como: Pulso, onda triangular, dente de serra e expandindo o
assunto para série cossenos e senos de Fourier. Mostrando a convergência da série através
do erro quadrático mínimo. Esse Trabalho de Conclusão de Curso (TCC) está apoiado em
programações feitas pelo software MATLAB por ser uma ferramenta bastante utilizada
nos problemas científicos e teóricos.
PALAVRAS-CHAVE: Função, Trigonometria, Frequência, Ortogonalidade, Séries,
Fourier, Coeficientes, Kronecker, Teorema, Corolário, Aplicação, Minimização,
Programação no MATLAB.
ABSTRACT
This paper begins with the definitions of periodic functions, trigonometric, sine
cycle, cosine, tangential, odd and even function and their proposals with corresponding
statements. Opening a range for the whole of even and odd functions. Then they have been
careful to set the frequency, period and characterize the difference between frequency and
angular frequency to introduce them in trigonometric series. It makes a brief history of
how Fourier came deductions of the coefficients of its series writing in his book
"Mathematical Theory of Heat Conduction," highlighting mathematicians who worked the
same idea, as Euler, Bernoulli, Taylor, Maclaurin and others . The following makes up a
display of orthogonal functions, showing an orthonormal system, less through these
concepts, Fourier coefficients, similarly using trigonometric identities to solve some
wholly peculiar to the subject, with the representation of the Kronecker Delta is the same
results for the Fourier coefficients. After the definition of piecewise function is discussed
the smooth functions of problems, very smooth, jumps and corners. Always trying to
demonstrate all theorems and corollaries containing continuous functions including the
series itself. Applying this theory in some functions such as pulse, triangle wave, saw tooth
and expanding it to cosine series and Fourier sines. Showing the convergence of the series
through the minimum square error. This Work Course Conclusion (TCC) is supported by
programs made by MATLAB software, a tool widely used in scientific and theoretical
problems.
KEYWORDS: Function, Trigonometric, Frequency, Orthogonality, Series, Fourier
coefficients, Kronecker, Theorem, Corollary, Application, Minimization, Programming in
MATLAB.
SUMÁRIO
INTRODUÇÃO ............................................................................................................................... 12
CAPÍTULO 1 ................................................................................................................................... 14
1•1 –FUNÇÃO PERIÓDICA ....................................................................................................... 14
1•1•1-Definição: ....................................................................................................................... 14
1•1•2-Proposição: ..................................................................................................................... 15
1•1•3-Proposição: ..................................................................................................................... 15
1•2-CICLO TRIGONOMÉTRICO. ............................................................................................. 16
1•2•1-Definição: ....................................................................................................................... 16
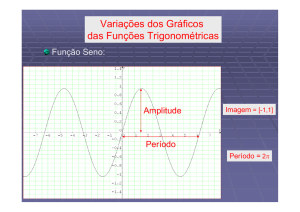
1•3 – FUNÇÃO SENO................................................................................................................. 17
1•3•1- Definição: ...................................................................................................................... 17
1•3•2- Proposição: .................................................................................................................... 17
1•4 – FUNÇÃO COSSENO ......................................................................................................... 19
1•4•1 – Definição:: ................................................................................................................... 19
1•4•2- Proposição: .................................................................................................................... 19
1•5 – FUNÇÃO TANGENTE ...................................................................................................... 20
1•5•1 – Definição: .................................................................................................................... 20
1•6 – FUNÇÃO PAR E ÍMPAR .................................................................................................. 21
1•6•1 – Definição: .................................................................................................................... 21
1•6•2 – Definição ..................................................................................................................... 23
CAPITULO 2 ................................................................................................................................... 24
2•1 FREQUÊNCIA ...................................................................................................................... 24
2•1•1-Definição: ....................................................................................................................... 24
2•2 – SÉRIES TRIGONOMÉTRICAS ........................................................................................ 24
2•3 – FUNÇÕES ORTOGONAIS ............................................................................................... 25
2•3•1- Proposição: .................................................................................................................... 26
2•4 – COEFICIENTES DE FOURIER ........................................................................................ 26
2•4•1- Proposição: .................................................................................................................... 27
2•5 – REPRESENTAÇÃO DELTA DE KRONECKER ............................................................. 30
2•5•1-Definição: ....................................................................................................................... 30
2•6 – RELAÇÕES DE ORTOGONALIDADE ........................................................................... 30
2•7 – DETERMINAÇÃO DOS COEFICIENTES DE FOURIER (a , a e
) ....................... 32
2•8 – DE OUTRA MANEIRA ..................................................................................................... 32
CAPITULO 3 ................................................................................................................................... 35
3•1 FUNÇÃO SECCIONALMENTE CONTÍNUA POR PARTES .......................................... 35
3•1•1-Definição: ....................................................................................................................... 35
3•2 TEOREMA 1 ......................................................................................................................... 35
3•3 DEMONSTRAÇÃO DO TEOREMA 1 ................................................................................ 36
3•4 COROLÁRIO 1 ..................................................................................................................... 36
3•5 TEOREMA 2: ESTIMATIVA DE ERRO ............................................................................. 36
3•6 DEMONSTRAÇÃO DO TEOREMA 2 ................................................................................ 37
3•7 TEOREMA 3 ......................................................................................................................... 37
3•8 DEMONSTRAÇÃO DO TEOREMA 3 ................................................................................ 37
3•9 TEOREMA 4 ......................................................................................................................... 38
3•10 DEMONSTRAÇÃO DO TEOREMA 4 .............................................................................. 38
3•11 COROLÁRIO 2 ................................................................................................................... 38
3•12 DEMONSTRAÇÃO DO COROLÁRIO 2 .......................................................................... 39
CAPITULO 4 ................................................................................................................................... 41
4•1 APLICAÇÃO......................................................................................................................... 41
4•1•1 FUNÇÃO PULSO .......................................................................................................... 41
Determinar a representação em Série de Fourier da função pulso de período
, dada por: .. 41
4•1•2 ONDA TRIANGULAR.................................................................................................. 44
Determinar a representação em Série de Fourier da Onda Triangular de período , dada por:
.................................................................................................................................................. 44
4•1•3 DENTE DE SERRA ....................................................................................................... 48
Determinar a representação em Série de Fourier da Onda “Dente de Serra” com período 2 , 48
CAPITULO 5 ................................................................................................................................... 51
5•1 MINIMIZAÇÃO DO ERRO QUADRÁTICO ...................................................................... 51
CAPITULO 6 ................................................................................................................................... 52
6•1 SÉRIE DE FOURIER COSSENOS E SENOS ..................................................................... 52
CONCLUSÃO ................................................................................................................................. 55
BIBLIOGRAFIA.............................................................................................................................. 57
LISTA DE FIGURAS
Figura 1-Função Periódica ................................................................................................................ 14
Figura 2 - Ciclo Trigonométrico ...................................................................................................... 17
Figura 3 - Função Seno. ................................................................................................................... 17
Figura 4 - Periodicidade da Função Seno......................................................................................... 18
Figura 5 - Função Cosseno. .............................................................................................................. 19
Figura 6 - Periodicidade da Função Cosseno ................................................................................... 20
Figura 7 - Função Tangente. ............................................................................................................ 20
Figura 8 - Periodicidade da Função Tangente .................................................................................. 21
Figura 9 - Variações do Cosseno...................................................................................................... 28
Figura 10 - Variações do Seno ......................................................................................................... 29
Figura 11 - Variações do Seno e Cosseno. ....................................................................................... 30
Figura 12 - Função Seccionalmente Contínua ................................................................................. 35
Figura 13 - Função Pulso ou Quadrática. ......................................................................................... 41
Figura 14 - Representação da Série de Fourier ................................................................................ 43
Figura 15 - Superposição da Função Pulso – Série de Fourier ........................................................ 44
Figura 16 – Onda Triangular ............................................................................................................ 44
Figura 17 - Série de Fourier da Onda Triangular ............................................................................. 47
Figura 18- Superposição da Onda Triangular - Série de Fourier ..................................................... 47
Figura 19 - Onda Dente de Serra ...................................................................................................... 48
Figura 20 - Série de Fourier da Dente de Serra ................................................................................ 50
Figura 21 - Superposição da Onda Dente de Serra - Série de Fourier ............................................. 51
12
INTRODUÇÃO
O trabalho partiu da ideia de fazer gráficos das séries desenvolvidas na matemática
utilizando o software MatLab, a partir de funções contínuas. Um dos primeiros objetivos
deste foi entender a periodicidade de funções. A ideia era descrever uma função como um
somatório, usando as séries de Potência, de Taylor ou de Maclaurin e culminou na
expansão trigonométrica de senos e cossenos. Essa ideia nasceu na história naturalmente
com Jean Baptiste Joseph Fourier (1768–1830) no começo do século
, quando
estudava o problema da condução de calor, fazendo um livro intitulado "Theorie
analytique de la chaleur" (Teoria Analítica do Calor).
No entanto ao longo dos estudos sobre o tema Série de Fourier, os objetivos foram
sendo adequados e optou-se por modelar os gráficos das funções periódicas e
seccionalmente contínua por partes, das variações de produtos de senos e cossenos, das
aplicações, manipulando o software MATLAB e mostrar a convergência e a continuidade
da Série de Fourier.
Inicialmente foi necessário, para clareza do mesmo, definir alguns conceitos de
matemática básica, como periodicidade das funções de valores reais e suas propriedades;
soma e produto de funções periódicas e multiplicação de um termo constante por funções
periódicas. Introduzindo o conceito de círculo trigonométrico, funções seno, cosseno e
tangente. Definindo-se funções pares e impares com suas respectivas proposições e
demonstrações.
Em seguida, foi exposto o conceito de frequência, que é o inverso do período, nesse
momento foi introduzido o tópico séries trigonométricas, que foram estudadas por
matemáticos com grande destaque na História, assim como Fourier que pesquisou e
calculou os coeficientes da série. Estes coeficientes são calculados manejando as funções
ortogonais, que por definição chegam aos termos gerais normalizando para todos os
coeficientes. Posteriormente, os resultados são particularizados para um coeficiente de
índice zero, par e impar. De modo análogo usando as fórmulas das identidades
trigonométricas muito úteis para a resolução de integrais presentes nesta monografia e após
a concepção do Delta de Kronecker e das relações de ortogonalidade que são fórmulas
13
recorrentes dessas identidades trigonométricas chegando ao mesmo resultado para os
coeficientes a , a e
.
Demonstrando os vários teoremas (1, 2 - Estimativa de Erro, 3 e 4) e corolários (1
e 2) de abrangência da Série de Fourier que tratam da continuidade e convergência das
funções contínuas. Logo adiante, conhecendo a função seccionalmente contínua por partes,
algumas aplicações foram apresentadas, tais como: Função pulso, Onda Triangular e a
Dente de Serra com os seus respectivos gráficos e suas séries de Fourier, correspondentes.
Apresentando ainda a minimização do erro quadrático e a expansão da Série de Fourier
seno e cosseno.
Apesar da complexidade do tema, espera-se que os docentes e discentes desta
Instituição Federal, principalmente da Matemática, Física e algumas Engenharias que
possuem como disciplina Tópicos da Matemática Aplicada possam tirar proveitos e
explorar o mesmo tanto para o conhecimento que esta monografia possa trazer como
comentar possíveis descontentamentos. De uma forma ou de outra que esses comentários
possam melhorar o teor dessa obra e que o autor se instrua cada vez mais com essas
observações vindas.
14
CAPÍTULO 1
Será abordado conceitos básicos de matemática de onde iniciará o trabalho.
1•1 –FUNÇÃO PERIÓDICA
1•1•1-Definição:
Uma função :
⟶
condição:
0 satisfazendo a
é periódica se existe um número
, ∀ ∈ 1.1
O menor valor de
que satisfaz a condição acima é chamado período de . O
gráfico da função periódica se caracteriza por apresentar um elemento da curva que se
repete, isto é, para desenhar toda a curva, basta esboçar um caminho que contenha o tal
elemento da curva e prosseguir. Período é o menor comprimento do caminho (medido no
eixo dos , como no gráfico a baixo).
%Programa 01 - Mostra a periodicidade da função y=f(x)
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-4:0.001:-2;y1=x1+4;
x2=-2:0.001:0;y2=x2+2;
x3= 0:0.001:2;y3=x3;
x4= 2:0.001:4;y4=x4-2;
plot(x1,y1,'ok',x2,y2,'or',x3,y3,'oy',x4,y4,'ob')
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Função Periódica (p=2)' )
grid
hold on
Função Periódica (p=2)
2
1.8
1.6
1.4
Y
1.2
1
0.8
0.6
0.4
0.2
0
-4
-3
-2
-1
0
X
Figura 1-Função Periódica
1
2
3
4
15
1•1•2-Proposição:
Se é uma função periódica de período , então:
●
a , para a ≠ 0 é periódica de período . Logo:
Suponha que
a
a
∗
∗
. Fazendo
a
seja o período de
a obtêm-se
a
é periódica de período , conclui-se que
,
●●
ara
a , de modo que
∗
⟹
∗
a
∗
seja o período de
. Fazendo,
obtêm-se
a
.
. Logo:
, logo pela hipótese de que
duas constantes reais quaisquer. Assim, a função ℎ definida por:
ℎ
Também, é periódica de período . De modo que:
ℎ
ℎ
,
,
,…,
Dada pela combinação linear de
e
sejam
1.2
1.3
, ∀ ∈ ℝ.
É obvio que a proposição é válida para o monômio
Generalizando, se
são funções periódicas de período . Então a função:
,
,
,…,
é
.
1•1•3-Proposição:
Se
são duas funções periódicas de mesmo período . Tal que
ℎ
∗
, de modo que
⟹
periódica de período , concluí-se que
a
. Logo pela hipótese de que
≠ 0 é periódica de período
Suponha que
a
⋯
(x)
1.4
também é periódica de período .
16
Para
, com
) é transformada numa função
≠ 0, ∀ ∈ ℝ . Seja
com período 2 , pois quando → 2 ⟹
Assim,
Fazendo;
2
2 ⟹
2
, pois quando
2
2
2
Trocando as variáveis
, de modo que a função
1
2
2
1
2
2
→ .
1
1.5
⇌ , as expansões de funções periódicas desse tipo terão período
⟶2 ⟹ ⟶ .
1•2-CICLO TRIGONOMÉTRICO.
1•2•1-Definição:
Seja o plano num sistema cartesiano ortogonal 0 e uma circunferência de centro
0 e raio
, então
= 1. Cujo comprimento da circunferência é 2 , sendo
também é imagem dos números:
Em resumo
números reais
imagem
e
2 ,
4 ,
−2 ,
−4 ,
6 ,
−6 ,
no ciclo são tais que
,∀
−
∈ℤe
2
são côngruos de módulo 2 , ou simplesmente
Os eixos
e
8 ,…
− 8 ,…
é a imagem dos elementos { ∈ ℝ ∕
2
a imagem do número
Ou
2
, ∀ ∈ ℤ}. Dois
2
,∀
e
são côngruos.
−
∈ ℤ que tem a mesma
e por isso diz-se que
dividem a circunferência em quatro quadrantes: I, II, III e IV. Dado
um número real , a seguinte linguagem é usada para efeito de localização da imagem
no ciclo:
Se
1.6
está no 1° quadrante ↔
∈
⟺ 0+ 2
≤
≤
2
;
de
17
Se
Se
Se
está no 2° quadrante ↔
∈
⟺
está no 4° quadrante ↔
∈
⟺
está no 3° quadrante ↔
∀ ∈ ℤ.
∈
⟺
2
≤
2
≤
2
≤
≤
2
≤
≤2
2
;
2
;
.
1.7
Figura 2 - Ciclo Trigonométrico
1•3 – FUNÇÃO SENO
1•3•1- Definição:
Dado um número real , seja
denotado por
função
a ordenada
a função
sua imagem no ciclo. Denomina-se seno de
do ponto
que associa a cada real
:ℝ ⟼ ℝ
⟼
em relação ao sistema
o real
. Denomina-se
, isto é:
,∀ ∈ ℝ
Figura 3 - Função Seno.
1•3•2- Proposição:
Se o seno é uma função periódica de período , então:
1.8
18
2
2
...
É periódica de período
⋯
2 ⁄ .
,∀
ℕ.
%Programa 02 - Mostra a periodicidade da função seno
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-4*pi:0.001:-2*pi;y1=sin(x1);
x2=-2*pi:0.001:0;y2=sin(x2);
x3= 0:0.001:2*pi;y3=sin(x3);
x4= 2*pi:0.001:4*pi;y4=sin(x4);
plot(x1,y1,'ok',x2,y2,'or',x3,y3,'oy',x4,y4,'ob')
axis([-14 14 -1.2 1.2])
xlabel( ' X ' ); ylabel( ' Y=SEN(X) ' ); % Rótulos dos Eixos
title('Função Seno' )
grid
hold on
Função Seno
1
0.8
0.6
Y=SEN(X)
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-10
-5
0
X
5
Figura 4 - Periodicidade da Função Seno.
10
1.9
19
1•4 – FUNÇÃO COSSENO
1•4•1 – Definição::
Dado um número real , seja
denotado por
função
a abscissa
sua imagem no ciclo. Denomina-se cosseno de
do ponto
em relação ao sistema
que associa a cada real , o real OP
a função
: ℝ ⟼ ℝ
⟼
=
. Denomina-se
, isto é:
1.10
,∀ ∈ ℝ
Figura 5 - Função Cosseno.
1•4•2- Proposição:
Se o cosseno é uma função periódica de período , então:
cos
cos
2
2
cos
cos
É periódica de período
...
2 ⁄ .
1.11
⋯
, ∀ .
%Programa 03 - Mostra a periodicidade da função cosseno
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-4*pi:0.001:-2*pi;y1=cos(x1);
x2=-2*pi:0.001:0;y2=cos(x2);
x3= 0:0.001:2*pi;y3=cos(x3);
x4= 2*pi:0.001:4*pi;y4=cos(x4);
plot(x1,y1,'ok',x2,y2,'or',x3,y3,'oy',x4,y4,'ob')
axis([-14 14 -1.2 1.2])
xlabel( ' X ' ); ylabel( ' Y=COS(X) ' ); % Rótulos dos Eixos
20
title('Função Cosseno' )
grid
hold on
Função Cosseno
1
0.8
0.6
Y=COS(X)
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-10
-5
0
X
5
10
Figura 6 - Periodicidade da Função Cosseno
1•5 – FUNÇÃO TANGENTE
1•5•1 – Definição:
Dado um número real ,
reta
e seja
e
≠
e seja
a sua imagem no ciclo. Considere a
a sua interseção com o eixo das tangentes de
medida algébrica dos segmentos
e
′. Assim:
1.12
Figura 7 - Função Tangente.
[indicado por
]a
21
%Programa 04 - Mostra a periodicidade da função tangente
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figura
x1=-2*pi:0.001:-pi;y1=tan(x1);
x2=-pi:0.001:0;y2=tan(x2);
x3= 0:0.001:pi;y3=tan(x3);
x4= pi:0.001:2*pi;y4=tan(x4);
plot(x1,y1,'ok',x2,y2,'or',x3,y3,'oy',x4,y4,'ob')
axis([-7 7 -10 10])
xlabel( ' X ' ); ylabel( ' Y=tg(X) ' ); % Rótulos dos Eixos
title('Função Tangente' )
grid
hold on
Função Tangente
10
8
6
4
Y=tg(X)
2
0
-2
-4
-6
-8
-10
-6
-4
-2
0
X
2
4
6
Figura 8 - Periodicidade da Função Tangente
1•6 – FUNÇÃO PAR E ÍMPAR
− ,∀
1•6•1 – Definição:
Uma função : ℝ ⟼ ℝ é par se, e somente se,
ℝ.
1•6•1•1- Proposição:
A soma ou diferença de duas funções pares é par.
Demonstração:
Considere as funções pares
definição e seja a função
−
.
e
tal que
então
±
−
e
−
−
±
, por
−
22
Logo,
é par.
1•6•1•2- Proposição:
O produto ou quociente de duas funções pares é par.
Demonstração:
Considere as funções pares
definição e seja a função
−
e
tal que
, então
⋇
.
−
e
−
⋇
−
, por
−
é par.
Logo,
1•6•1•3- Proposição:
O produto ou quociente de duas funções ímpares é par.
Demonstração:
Considere as funções impares
−
−
e
, por definição e seja a função
⋇ −
Logo,
é par.
⋇
, então
tal que
−
−
−
−
⋇
−
−
1•6•1•4- Proposição:
A soma ou a diferença de uma função par com uma função ímpar não é par nem
ímpar.
Demonstração:
Considere a função
par e
impar, então
por definição e seja a função
−
⇒
não é par nem ímpar.
1•6•1•5- Proposição:
Se
tal que
é par, então
Demonstração:
Considere a função
par,
ã
2∙
−
±
−
.
− , por definição e seja:
−
−
,
±
23
†
−
−
−
− −
.
Logo:
⇒ de † , obtêm-se:
2
1•6•2 – Definição:
Uma função : ℝ ⟼ ℝ é ímpar se, somente se,
=
, ∀ ℝ.
1•6•2•1 – Proposição:
A soma ou diferença de duas funções ímpares é ímpar.
Demonstração:
e Considere as funções
impares, então ), por definição e seja a função
Logo,
=
é impar.
=
=
e =
tal que
=
=
1•6•2•2 – Proposição:
O produto ou o quociente de uma função par e uma função impar é uma função impar.
Demonstração:
Demonstração:
Considere a função
par e
por definição e seja a função
==
Logo,
.
é impar.
impar, então
tal que
=
=
⋇
=
=
,
⋇
24
1•6•2•3 – Proposição:
Se
.
é impar, então
Demonstração:
Considere as funções
−
††
0
−
e
−
funções ímpares, assim
, por definição e seja:
=
0
=
=
0
−
e
0
⟹ de †† obtém-se:
−
.
0
CAPITULO 2
2•1 FREQUÊNCIA
2•1•1-Definição:
A frequência
de uma função periódica
é definida como o inverso de seu
período e dá o número de repetições ou ciclos em cada intervalo fundamental de período
em . Se,
é medido em segundos então a frequência F é o número de ciclos por segundo,
ou seja, Hertz (Hz); outra frequência é a angular denotada por
Fazendo o período fundamental
dada por
, obtêm-se:
2
1
2
2.1
⁄
.
2.2
2•2 – SÉRIES TRIGONOMÉTRICAS
A ideia de compor funções através das funções trigonométricas seno e cosseno foi
estudada por grandes matemáticos como: Euler, Bernoulli, D’Alembert, Lagrange,
Dirichlet, Riemann, etc... Porém, foi Jean Baptiste Joseph Fourier 1768 − 1830) que na
tentativa de resolver a equação de onda
⁄
=
∇
, onde: ( ,
,
,…,
, )éa
25
uma constante fixa e ∇ o Laplaciano. Explicitou os coeficientes de tais
função escalar,
séries e escreveu as séries seno e cosseno de várias funções em seu trabalho intitulado
“Teoria Matemática de Condução do Calor”. Seja
período fundamental
Logo:
~a
2
, de modo que
a
b
a
~a
3
a
~
a
b
a
3
a frequência correspondente ao
⟹
2
,
, sendo
⋯
.
2
∀ ∈ {0 ∪ ℕ
2.3
, ∀ ∈ {0 ∪ ℕ
b
A série 2.3 é dita ser a Série Trigonométrica de Fourier de Funções Ortogonais
com periodicidade 2 .
2•3 – FUNÇÕES ORTOGONAIS
Para representar uma função
são funções ortogonais no intervalo
seguintes condições:
<
∑
em série do tipo:
,
, onde
, essas funções ortogonais devem satisfazer as
0,
∙
0,
≠
2.4
A norma de um sistema de função ortogonal é dada por:
‖
i.e., ‖
‖
<
∙
a
2.5
Um sistema ortogonal diz-se ortonormado quando sua norma é igual à unidade,
‖
1.
26
,
2•3•1- Proposição:
∑
Seja
converge no intervalo a,
≤
, obtêm-se:
∙
<
∙
a
‖
Logo,
Onde os
`
‖
par ⇒
‖
⇒
=
‖
ímpar ⇒
‖
<
⇒
=
‖
2.6
‖
e cos
<
⇒
‖
∙
=1⇒‖
‖
∙
1
2
‖
‖
. Assim para:
2 .
1
2
‖
a
2
.
>
1
2
1
=
, ∀ ∈ {0 ∪ ℕ , onde
a cos
são funções ortogonais reais
0⇒
∙
‖
a
denominam-se os Coeficientes de Fourier.
2•4 – COEFICIENTES DE FOURIER
∑
Considere a série
~a
, com as seguintes hipóteses a série
e converge para . Assim, fazendo o produto interno da série
em ambos os lados por
<
a≤
1
cos 2
∙ cos
.
1 − cos 2
1
2
2
1
2
2
2.7
a
0 =
0 =
2.8
27
<
‖
∙
>
‖
1
∙ sen
b
2.9
2•4•1- Proposição:
Da trigonometria elementar as fórmulas para o seno e cosseno da soma e da
diferença, respectivamente, são:
∙
∙
2.10)
( + )=
∙
−
∙
(2.11)
( − )=
∙
+
∙
(2.13)
( − )=
∙
−
∙
(2.12)
A partir destas equações obter-se-ão quatro identidades úteis para a resolução de
algumas integrais encontradas mais adiante neste trabalho.
De (2.11) + (2.13) ⇒ 2 ∙
∙
=
( + )+
( − )
%Programa 05 - Mostra as variações das funções cos(nx) e cos(mx)
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
n=[1; 2];
m=[2; 3];
x=-pi:0.001:pi;
y=cos(n*x);
subplot(2,2,1)
plot(n*x,y,'k')
grid
xlabel('nx'); ylabel('cos(nx)')
title( 'Variação da Função Cosseno' )
z=cos(m*x);
subplot(2,2,2)
plot(m*x,z,'y')
grid
xlabel('mx'); ylabel('cos(mx)')
title( 'Variação da Função Cosseno' )
w=2*cos(n*x).*cos(m*x);
subplot(2,2,3)
plot(x,w,'b')
grid
xlabel('x'); ylabel('2*cos(nx)*cos(mx)')
title( 'Variação do Produto dos Cossenos' )
P=(cos(m*x)).^2;
subplot(2,2,4)
(2.14)
28
plot(m*x,P,'r')
grid
xlabel('mx'); ylabel('(cos(mx)).^2')
title( 'Quadrado do Cosseno' )
hold on
Variação da Função Cosseno
1
0.5
0.5
cos(mx)
cos(nx)
Variação da Função Cosseno
1
0
-0.5
-1
-10
-0.5
-1
-10
-5
1
0
-1
-2
0
x
2
4
-5
0
5
mx
Quadrado do Cosseno
10
1
(cos(mx)). 2
2*cos(nx)*cos(mx)
0
5
10
nx
Variação do Produto dos Cossenos
2
-2
-4
0
0.5
0
-10
-5
0
mx
5
10
Figura 9 - Variações do Cosseno
De 2.13 − 2.11 ⇒ 2 ∙
∙
−
−
%Programa 06 - Mostra as variações das funções sen(nx) e sen(mx)
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
n=[1; 2];
m=[2; 3];
x=-pi:0.001:pi;
y=sin(n*x);
subplot(2,2,1)
plot(n*x,y,'k')
grid
xlabel('nx'); ylabel('sen(nx)')
title( 'Variação da Função Seno' )
z=sin(m*x);
subplot(2,2,2)
plot(m*x,z,'y')
grid
xlabel('mx'); ylabel('sen(mx)')
title( 'Variação da Função Seno' )
w=2*sin(n*x).*sin(m*x);
subplot(2,2,3)
plot(x,w,'b')
grid
xlabel('x'); ylabel('2*sen(nx)*sen(mx)')
title( 'Variação do Produto dos Senos' )
P=(sin(m*x)).^2;
subplot(2,2,4)
plot(m*x,P,'r')
grid
xlabel('mx'); ylabel('(sen(mx)).^2')
title( 'Quadrado do Seno' )
hold on
2.15
29
Variação da Função Seno
1
0.5
0.5
sen(mx)
sen(nx)
Variação da Função Seno
1
0
-0.5
-0.5
-1
-10
-1
-10
0
5
10
nx
Variação do Produto dos Senos
-5
2
1
0
-1
-2
-4
-5
0
5
mx
Quadrado do Seno
10
-5
10
1
(sen(mx)). 2
2*sen(nx)*sen(mx)
0
-2
0
x
2
0.5
0
-10
4
0
mx
5
Figura 10 - Variações do Seno
De 2.10) − (2.12) ⇒ 2 ∙
De (2.10) + (2.12) ⇒ 2 ∙
∙
∙
=
=
( + )−
( + )+
( − )
( − )
%Programa 07 - Mostra as variações das funções sen(nx) e cos(mx)
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
n=[1; 2];
m=[2; 3];
x=-pi:0.001:pi;
y=sin(n*x);
subplot(2,2,1)
plot(n*x,y,'k')
grid
xlabel('nx'); ylabel('sen(nx)')
title( 'Variação da Função Seno' )
z=cos(m*x);
subplot(2,2,2)
plot(m*x,z,'y')
grid
xlabel('mx'); ylabel('cos(mx)')
title( 'Variação da Função Cosseno' )
w=2*sin(n*x).*cos(m*x);
subplot(2,2,3)
plot(x,w,'b')
grid
xlabel('x'); ylabel('2*sen(nx)*cos(mx)')
title( 'Variação do Produto' )
hold on
(2.16)
(2.17)
30
Variação da Função Cosseno
1
0.5
0.5
cos(mx)
sen(nx)
Variação da Função Seno
1
0
-0.5
-1
-10
0
-0.5
-5
0
5
nx
Variação do Produto
-1
-10
10
-5
0
mx
5
10
2*sen(nx)*cos(mx)
2
1
0
-1
-2
-4
-2
0
x
2
4
Figura 11 - Variações do Seno e Cosseno.
2•5 – REPRESENTAÇÃO DELTA DE KRONECKER
2•5•1-Definição:
É uma representação matemática definida por:
1,
0,
≠
2.18
2•6 – RELAÇÕES DE ORTOGONALIDADE
Seja
Para
se;
,
≠
ℕ. Logo:
segue que
cos
∙
, usando a identidade 2.14 obtêm-
31
cos
Para
∙
1
2
2
1
1
, segue
=
1
2
∥
1
2
2
cos
Para
se;
≠
Para
=
2
∙
,
1
2
1
−
segue
1
−
1
2
1
2
1
1
2 −
2
2
ℕ⇒
1
2
2
−
−
0
∥
0 =
∙
∙
2.19
, usando a identidade 2.15 obtêm-
−
sen
2
∙
sen
1
−
1
−
∙ cos
2
−
que
sen
Para todo ,
∙
sen
, segue que
sen
cos
que
−
∙
−
∥
−
∙ sen
∙
−
1
1
∥
1
2 −0 =
2
0
−
2.20
, usando a identidade 2.16 ou
2.17 aqui se usa a 2.16 e a 2.17 fica para o leitor verificar como exercício,
assim;
32
sen
∙ cos
1
−
2
−
1
−
1
2
1
∥
sen
∙
1
−
1
−
−
−
−
−
2.21
0
2•7 – DETERMINAÇÃO DOS COEFICIENTES DE FOURIER (a , a e
Observando a equação 2.7 em
no intervalo de 0,
Observando a equação 2.8 em
no intervalo de 0,
a
a
Observando a 2.9 em
b
2
2
0
)
, têm-se:
2.22
, têm-se:
∙
no intervalo de 0,
2
∥
∙
2.23
, têm-se:
2.24
2•8 – DE OUTRA MANEIRA
Observando a série 2.3 e fazendo
2,3 no intervalo
,
, tem-se que:
2 e integrando ambos os lados de
33
a
2
a
Observando que:
a
a
=
∀
∈ ℕ. Logo: a
∥
, têm-se:
a
2
a
2
Observando que:
2
a
=
−
0
= 0;
0
2.25
= 0.
ambos os lados de 2.3 no intervalo de
Integrando e multiplicando por
0,
a
∥
a
a
∥
=a ∙
∙
2
a
=a ∙ ∙
0, de 2.21 .
−
, de 2.19 ;
0
= 0;
34
∀
∈ ℕ. Logo: a
2.26
ambos os lados de 2.3 no intervalo
Integrando e multiplicando por
de 0,
, têm-se:
a
2
a
2
Observando que:
a
∀
−
2
a
a
∈ ℕ. Logo:
∥
−
= 0, de 2.21 ;
b ∙
2
∙
a
−
∙ ∙
2.27
0
= 0;
, de 2.20 .
Até aqui, não houve uma preocupação em relação aos passos do conceito da Série
de Fourier apenas ficou definido que é uma série do tipo 2.3 e que as integrais para os
cálculos dos coeficientes a , a e
existem, para isto é suficiente que
exceto para um número finito de saltos entre –
contínua.
e
, ou seja,
seja contínua
é seccionalmente
35
CAPITULO 3
3•1 FUNÇÃO SECCIONALMENTE CONTÍNUA POR PARTES
3•1•1-Definição:
Uma função
é seccionalmente contínua por partes em um intervalo a,
se
ela é contínua em todo o intervalo, exceto em um número finito de pontos:
a≤
<
<
<⋯<
≤
seja contínua em cada subintervalo aberto
De modo que
Obviamente toda função contínua é seccionalmente contínua por partes.
<
< ,∀
ℕ.
%Programa 08 - Função Seccionalmente Contínua
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-2*pi:0.001:-pi;y1=-0.5*cos(x1);
x2=-pi:0.001:0;y2=0.5*cos(x2);
x3= 0:0.001:pi;y3=-0.5*cos(x3);
x4= pi:0.001:2*pi;y4=0.5*cos(x4);
plot(x1,y1,'ob',x2,y2,'ob',x3,y3,'ob',x4,y4,'ob')
axis([-7 7 -1 1])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Função Seccionalmente Contínua' )
grid
hold on
Função Seccionalmente Contínua
1
0.8
0.6
0.4
Y
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-6
-4
-2
0
X
2
4
6
3•2 TEOREMA 1
Figura 12 - Função Seccionalmente Contínua
A soma de uma série uniformemente convergente de funções contínuas é contínua;
isto é; se cada
é contínua em a ≤
≤
que a série convirja uniformemente em a ≤
⇒
≤ .
∑
é contínua, contanto
36
3•3 DEMONSTRAÇÃO DO TEOREMA 1
a, e
0⇒∃
0 tal que |
Dados
suficientemente grande para que: ⊛ |
Fazendo
≥
|<
⋯
, onde:
quando |
|<
. Assim a função
,∀
a,
|< .
com
é a soma de
um número finito de funções contínuas, logo é contínua. Portanto,
⊛⊛ |
De ⊛, tem-se: |
|
|
−
≤|
<
|
1
3
−
−
−
−
1
3
|
∑
Logo:
|<
|<
1
3
, ∀
e|
|
|
−
, para | −
−
−
|<
|
−
|< .
|<
|
. De modo que:
−
−
a, b é contínua e converge para
|≤
|<
.
3•4 COROLÁRIO 1
a≤
Se
≤
∑
∑
e
e são contínuas em a,
são uniformemente convergente para
. Então a série:
É contínua e uniformemente convergente, ∀ a ≤
≤ .
3•5 TEOREMA 2: ESTIMATIVA DE ERRO
Se |
|≤
em a,
⇒
a
≤
−a .
37
3•6 DEMONSTRAÇÃO DO TEOREMA 2
Aplicando a desigualdade triangular inúmeras vezes, conclui-se que:
Como |
|
|
∆
|∆
, por hipótese têm-se no máximo que:
|
|∆
∆
∆
− a)
Logo:
( )∆
lim
→
∆ →
( − a) ⇒
( − a)
a
3•7 TEOREMA 3
Uma série uniformemente convergente de funções contínuas pode ser integrada
é contínua em a,
termo a termo, isto é, se cada
a
+
a
( )
a
+
. Então:
( )
a
É contínua e converge uniformemente ∀a
+ ⋯+
a
=
a
Logo, ∀ > 0∃
Escolhendo um
( )
∈
∈
+
( )
a
tal que
a
a
+⋯
.
3•8 DEMONSTRAÇÃO DO TEOREMA 3
Faça ( ) ser a − é
soma parcial da série ∑
( )
( )
+
( )
a
−
( ). Então:
+ ⋯+
a
suficientemente grande de modo que:
a
, ∀
( )
.
38
|
|<
−
−a
;∀
≥
a ≤ x ≤b
Portanto, usando o TEOREMA 2, encontra-se:
−
a
a
a
Assim,
a
→
−
a
a
a
−
≤
< ;∀
≥
−a
∙
−a
.
, converge e é contínua em a,
.
3•9 TEOREMA 4
Toda série trigonométrica uniformemente convergente é uma Série de Fourier.
Mais precisamente, se a série 2.3 converge uniformemente a
,∀
ℝ ⇒
é
contínua ou seccionalmente contínua, tem período 2 e a série 2.3 é a Série de Fourier
de
.
3•10 DEMONSTRAÇÃO DO TEOREMA 4
Visto que a série 2.3 converge uniformemente para todo , sua soma
pelo
TEOREMA 1 é contínua para todo . A série permanece uniformemente convergente se
os seus termos são multiplicados por cossenos ou senos, pelo COROLÁRIO 1 do
TEOREMA 1. Desse modo a integração termo a termo é justificada pelo TEOREMA 3,
segue previamente que a série 2.3
em questão é uma SÉRIE DE FOURIER de
e
sua periodicidade é uma consequência da periodicidade dos termos da série como
observado no CAPÍTULO 2, TÓPICO 2•2.
3•11 COROLÁRIO 2
Se duas ou mais série trigonométricas convergem uniformemente ∀ e têm a
mesma soma ∀ , ou seja:
39
a
2
a
à
2
b
Logo, as séries são idênticas. Assim:
a
à ; a
à e
à
.
,∀
ℕ.
3•12 DEMONSTRAÇÃO DO COROLÁRIO 2
Se
é a Soma de ambas as Séries. Então, pelo TEOREMA 4, têm-se:
a
a
à
à
1
1
;
e
1
E assim sucessivamente.
Embora a série de Fourier seja bem definida para funções
contínuas, esse
conceito pode ser extentido para funções seccionalmente continuas por partes e funções
que contenham saltos verificando que pouco é necessário para também asseguar a
é periódica com período 2 e
convergência das mesmas para
. Em particular, se
convergirá uniformemente para
. O resultado por si só é notável quando se considera o
têm derivadas primeira e segunda contínuas ∀ , então a série de Fourier de
fato de que a expansão de
em uma série de potências requer derivadas contínuas de
todas as ordens para sua convergência. Pode-se ainda ir mais longe e garantir a
convergência uniforme da série de Fourier para
pontos em que ′
quando
tem descontinuidade de saltos,
tem "cantos", isto é, os
tem derivadas primeira e
segunda contínuas entre esses cantos, como está ilustrado na Fig. 4.4. Na verdade, pode-se
expandir o conceito de canto para incluir saltos de descontinuidades de
, como
ilustrado na Fig. 4.1. Dificilmente pode-se esperar convergência da série de Fourier para
nos pontos de descontinuidade, onde
pode até ser definida de forma ambígua.
Entretanto a série de Fourier faz essa convergência naturalmente e de forma razoável
40
levando a convergência para a média entre os limites à esquerda e à direita, isto é, para o
.
número na descontinuidade
1
lim
2 →
lim
→
Não se pode esperar que a série de Fourier convirjá uniformemente numa
vizinhança de descontinuidade, mas irá convergir uniformemente em todo intervalo
fechado que não contenha descontinuidade.
Embora tenha sido considerado até este ponto apenas funções periódicas
com períodicidade 2 , deve ser observado que as fórmulas para os coeficientes de Fourier
2.7 , 2.8 e 2.9 utiliza somente os valores de
entre − e . Assim, se
for
dada apenas nesse intervalo, e for, por exemplo, contínua, então a série de Fourier
correspondente pode ser formada e chamar-se-á série de Fourier de
entre –
converge para
. Se a série
e , então ela irá convergir para fora do intervalo da função
que é a extensão periódica de
. Deve ser observado que, a menos que
o processo de extensão introduzirá descontuidades de salto em
a série convergirá para um número médio entre os dois valores.
e
−
,
− , nesse caso
Uma funçaõ seccionalmente contínua por partes no intervalo
como
definida na seção 3.1 tem limites finitos nas extremidades do subintervalo. Por
conseguinte, no interior do i-ésimo subintervalo a função
é contínua em cada
subintervalo fechado, se, além disso, a função possuir primeira derivada contínua, o termo
é uma função por partes suave. Se, além disso, a função possuir derivadas segundas
contínuas, diz-se-á que
é uma função muito suave por partes. Se
muito suave por partes no intervalo −
converge a
. Então a Série de Fourier de
em todo ponto interior em que
convergirá para:
1
lim
2 →
é uma função
é continua. Assim, a série de Fourier
lim
→
Em todo ponto de descontinuidade interior ao intervalo para:
em
1
lim
2 →
lim
→
. A convergencia é uniforme em cada intervalo fechado que não contenha
descontinuidades.
41
CAPITULO 4
4•1 APLICAÇÃO
4•1•1 FUNÇÃO PULSO
Determinar a representação em Série de Fourier da função pulso de período
por:
−1,
− < ≤0
4.1
1,
0< ≤ .
%Programa 09 - Função Pulso
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-3*pi:0.001:-2*pi;y1=-1;
x2=-2*pi:0.001:-pi;y2=1;
x3= -pi:0.001:0;y3=-1;
x4= 0:0.001:pi;y4=1;
x5=pi:0.001:2*pi;y5=-1;
plot(x1,y1,'ok',x2,y2,'ok',x3,y3,'ok',x4,y4,'ok',x5,y5,'ok')
axis([-3*pi 2*pi -2 2])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Função Pulso' )
grid
hold on
Função Pulso
2
1.5
1
Y
0.5
0
-0.5
-1
-1.5
-2
-8
-6
-4
-2
0
2
4
6
X
Figura 13 - Função Pulso ou Quadrática.
Calculando os coeficientes de Fourier, têm-se:
a
1
2
1
2
−1
1
1
−
2
0;
, dada
42
1
a
=
1
1
1
−
1
2
4
;
−1
1 1−
−1
−
1−
⇒
4
;
3
0;
Logo:
4
3
1
0;
1
−1
−
1 2−2
−1,
1,
0;
2 −1
2 −1
5
4
;
5
,∀
ℕ
éí
é
7
0;
⇑
⇐ 4.2
%Programa 10 - Série de Fourier da Função Pulso
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x=-3*pi:0.001:2*pi;
y=(4/pi)*sin(x)+(4/3*pi)*sin(3*x)+(4/5*pi)*sin(5*x);
plot(x,y,'og')
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Série de Fourier da Função Pulso' )
grid
hold on
4
;…
7
9
⋯
43
Série de Fourier da Função Pulso
8
6
4
Y
2
0
-2
-4
-6
-8
-10
-8
-6
-4
-2
0
2
4
6
8
X
Figura 14 - Representação da Série de Fourier
Fazendo a sobreposição gráfica da Função Pulso em sua Série de Fourier, observa-
se a aproximação limite da série, multiplicando 4.1 por −1 não altera a Onda
Quadrática apenas modifica sua pulsação, i.e., se o nível for alto ficará baixo e quando for
baixo ficará alto, ou vice-versa. Para { ∈ ℝ ∕
0+
, ∀ ∈ ℤ} em 4.2 , cada soma
parcial vale zero de modo que a série de fato converge para o valor médio dos saltos que é
zero. Sendo essa aproximação pior nas vizinhanças imediatas a esquerda e a direita dos
pontos de saltos.
%Programa 11 - Superposição da Função Pulso com sua série de Fourier
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x=-3*pi:0.001:2*pi;
x1=-3*pi:0.001:-2*pi;y1=1;
x2=-2*pi:0.001:-pi;y2=-1;
x3= -pi:0.001:0;y3=1;
x4= 0:0.001:pi;y4=-1;
x5=pi:0.001:2*pi;y5=1;
y=(4/pi)*sin(x)+(4/3*pi)*sin(3*x)+(4/5*pi)*sin(5*x);
plot(x,y,'g',x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b',x5,y5,'b')
axis([-3*pi 2*pi -7 7])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Superposição da Função Pulso com sua Série de Fourier' )
legend('Série de Fourier','Função Pulso')
hold on
44
Superposição da Função Pulso com sua Série de Fourier
Série de Fourier
Função Pulso
6
4
Y
2
0
-2
-4
-6
-8
-6
-4
-2
0
2
4
6
X
Figura 15 - Superposição da Função Pulso – Série de Fourier
4•1•2 ONDA TRIANGULAR
Determinar a representação em Série de Fourier da Onda Triangular de período ,
dada por:
− ,
−1< <0
4.3
,
0≤ <1
%Programa 12 - Onda Triangular
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-2:0.001:-1;y1=x1+2;
x2=-1:0.001:0;y2=-x2;
x3= 0:0.001:1;y3=x3;
x4= 1:0.001:2;y4=-x4+2;
plot(x1,y1,'ok',x2,y2,'ok',x3,y3,'ok',x4,y4,'ok')
axis([-2.5 2.5 -0.5 1.5])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Onda Triangular' )
grid
hold on
Onda Triangular
1.5
Y
1
0.5
0
-0.5
-2.5
-2
-1.5
-1
-0.5
0
X
0.5
1
Figura 16 – Onda Triangular
1.5
2
2.5
45
Calculando os coeficientes de Fourier, têm-se:
a =
a =
a =−
1
2
1
2
1
4
−
0−1
1
1
1
2
4
−
2
1
1
1+1 = ;
4
2
−
−1 ⇒
;a = 0;a = −
Logo:
1−0
1
−
2
2
0, é
−2, é
−1
4
4
4
;a = 0;a = −
;a = 0;a = −
;…
9
25
49
−
−
3
−
5
∙
0
1
−
1
1
∙
0
−
1
7
1
1
−⋯
46
1
1
1
=
=
=
=
−
=
=
=
=
1 4
−
2
−
∙
0+
=
0
+
=
+
∙
=
+
=
0 +
2 −1
2 −1
=
,∀
+0=
ℕ
%Programa 13 - Série de Fourier da Onda Triangular
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x=-2:0.001:2;
y=(1/2)-(4/(pi^2))*cos(pi*x)-(4/9*(pi^2))*cos(3*pi*x)(4/25*(pi^2))*cos(5*pi*x)-(4/49*(pi^2))*cos(7*pi*x)(4/81*(pi^2))*cos(9*pi*x)-(4/121*(pi^2))*cos(11*pi*x);
plot(x,y,'og')
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Série de Fourier da Onda Triangular' )
grid
hold on
+0=
⇑
⇐ 4.4
47
Série de Fourier da Onda Triangular
10
8
6
4
Y
2
0
-2
-4
-6
-8
-2
-1.5
-1
-0.5
0
X
0.5
1
1.5
2
Figura 17 - Série de Fourier da Onda Triangular
Fazendo a sobreposição gráfica da Onda Triangular em sua Série de Fourier,
observa-se a aproximação limite usando apenas dois termos da série. Espera-se
convergência por toda parte, inclusive converge para o valor médio quadrático dos saltos
1⁄2, exceto nos pontos de inflexão onde a convergência é mais fraca devido aos saltos.
%Programa 14 - Superposição da Onda Triangular com sua Série de Fourier
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x=-2:0.001:2;
x1=-2:0.001:-1;y1=x1+2;
x2=-1:0.001:0;y2=-x2;
x3= 0:0.001:1;y3=x3;
x4= 1:0.001:2;y4=-x4+2;
y=(1/2)-(4/(pi^2))*cos(pi*x);
plot(x,y,'g',x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b')
axis([-2.5 2.5 -0.5 1.5])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Superposição da Onda Triangular com sua Série de Fourier')
legend('Série de Fourier','Onda triangular')
hold on
Superposição da Onda Triangular com sua Série de Fourier
1.5
Série de Fourier
Onda triangular
Y
1
0.5
0
-0.5
-2.5
-2
-1.5
-1
-0.5
0
X
0.5
1
1.5
2
2.5
Figura 18- Superposição da Onda Triangular - Série de Fourier
48
4•1•3 DENTE DE SERRA
Determinar a representação em Série de Fourier da Onda “Dente de Serra” com
período 2 , dada por:
, ∀
,
4.5
%Programa 15 - Função "Dente de Serra"
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-3*pi:0.001:-pi;y1=x1+6;
x2=-pi:0.001:pi;y2=x2;
x3= pi:0.001:3*pi;y3=x3-6;
plot(x1,y1,'ok',x2,y2,'ok',x3,y3,'ok')
axis([-10 10 -6 6])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Dente de Serra' )
grid
hold on
Dente de Serra
6
4
Y
2
0
-2
-4
-6
-10
-8
-6
-4
-2
0
X
2
4
6
8
10
Figura 19 - Onda Dente de Serra
Calculando os coeficientes de Fourier, têm-se:
a
1
2
1
2
1
2
2
1
2
− −
2
0;
49
1
a
∙
∙
0;
=
=
∙
+
=
=
1
−
−
2;
2
0
1
∙
Logo:
1
2
−1;
−
2
2
∙
− ∙
2
2
2
;
3
2
2
3
+
0
=
=0
∙
∙
2
− ,
∙
∙
1
− ;
2
3
−1
2
−
−
2
4
−
−
2
2
;
5
4
1
− ;
3
2
5
5
⇑
⇐ 4.6
,
−
2
2
2
;
7
−
−
,
,
2
6
1
− ;…
4
6
⋯
%Programa 16 - Fourier da "Dente de Serra"
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x=-3*pi:0.001:3*pi;
y=2*sin(x)-(2/2)*sin(2*x)+(2/3)*sin(3*x)-(2/4)*sin(4*x)+(2/5)*sin(5*x)(2/6)*sin(6*x);
plot(x,y,'og')
50
% axis([-10 10 -6 6])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Fourier da Dente de Serra' )
grid
hold on
Fourier da Dente de Serra
4
3
2
Y
1
0
-1
-2
-3
-4
-10
-8
-6
-4
-2
0
X
2
4
6
8
10
Figura 20 - Série de Fourier da Dente de Serra
Fazendo a sobreposição gráfica da Onda Dente de Serra em sua Série de Fourier,
observa-se a aproximação limite usando seis termos da série. Novamente, para { ∈ ℝ ∕
0+
, ∀ ∈ ℤ} em 4.6 , cada soma parcial dessa série vale zero de modo que a
série converge para o valor médio dos saltos que é zero. Sendo essa aproximação piora nas
vizinhanças imediatas a esquerda e a direita dos pontos de saltos.
:
%Programa 17 - Superposição da Função "Dente de Serra" com sua Fourier
clear all; % ==> Limpa área de trabalho
close all; % ==> Fecha todas as janelas de figuras
x1=-3*pi:0.001:-pi;y1=x1+6;
x2=-pi:0.001:pi;y2=x2;
x3= pi:0.001:3*pi;y3=x3-6;
x=-3*pi:0.001:3*pi;
y=2*sin(x)-(2/2)*sin(2*x)+(2/3)*sin(3*x)-(2/4)*sin(4*x)+(2/5)*sin(5*x)(2/6)*sin(6*x);
plot(x,y,'g',x1,y1,'b',x2,y2,'b',x3,y3,'b')
legend('Série de Fourier','Onda Dente de Serra')
axis([-10 10 -6 6])
xlabel( ' X ' ); ylabel( ' Y ' ); % Rótulos dos Eixos
title( 'Superposição da Dente de Serra com sua Série de Fourier' )
hold on
51
Superposição da Dente de Serra com sua Série de Fourier
6
Série de Fourier
Onda Dente de Serra
4
Y
2
0
-2
-4
-6
-10
-8
-6
-4
-2
0
X
2
4
6
8
10
Figura 21 - Superposição da Onda Dente de Serra - Série de Fourier
CAPITULO 5
5•1 MINIMIZAÇÃO DO ERRO QUADRÁTICO
Nas aplicações foram feitas o procedimento formal, calcula-se os coeficientes e
mostra-se graficamente que a série converge para
. Agora, verificando esse processo
com mais cuidado, tem-se que o termo constante a ⁄2 da série é dado pela fórmula:
a
2
1
2
5.1
O segundo membro de 5.1 é simplesmente a média de
intervalo − ≤
≤ , de outra maneira. Observa-se que:
Isto é, a reta
reta. Assim a reta
−
a
2
0
e escrevendo essa no
5.2
a é tal que a área entre essa reta e a curva
a é uma espécie de reta de simetria para o gráfico
Outro ponto a considerar é o erro quadrático total da função
, definida como:
, abaixo da
.
em relação à
52
Esse erro é zero quando
−
5.3
ou quando
exceto num número finito de
pontos e é sempre positivo. Quer-se calcular uma função constante
seja o menor possível. Ou seja, quer se aproximar
do erro quadrático mínimo por uma constante
2
2
e
De modo que
o melhor possível, em termos
. Assim,
2
Onde:
5.4
são constantes.
tem um mínimo quando:
2 +4
0⇒
tal que esse erro
=
2
=
1
2
⁄
a
2
Como observado nas alíneas 4.1.1 , 4.1.2 e 4.1.3 .
0. Logo:
5.5
CAPITULO 6
6•1 SÉRIE DE FOURIER COSSENOS E SENOS
2
A série de Fourier até agora, tem sido considerada apenas paras funções de período
ou, mais restritamente, para funções definidas entre –
. Tais procedimentos
podem ser ampliados para o engrandecimento dessa teoria.
Se
entre
≤
≤
é uma função de período 2 , pode se usar um intervalo básico qualquer
2 , isso é, um intervalo de comprimento 2 . Para tal intervalo, o
mesmo raciocínio acima leva a uma série de Fourier, dada por:
a
Onde
a cos
b sen
5.1
53
1
a
f x cos
1
5.2
f x sen
5.3
é dado ∀ , com período 2 , isso é meramente um caminho análogo para o
Se
cálculo dos coeficientes a e . Se
neste intervalo; então se converge ela representa a extensão
ser utilizado para representar
periódica de
fora desse intervalo.
O intervalo −
simétricas. Faça
tem certas vantagens para a utilização de propriedades
ser definida neste intervalo e seja:
−
, para −
Então é chamada uma função par de
=
Então
=
a
a
no intervalo dado. Se, por outro lado:
≤
, para
≤ 5.5
0,se éimpar
2
, se épar
a
Faça agora ser par no intervalo
5.4
é chamada uma função ímpar de .
Além disso,
que
2 , a série pode
é dada apenas para
5.6 . Então
é impar, ver tópico 1.6. Portanto por 5.6 , obtêm-se:
a
2
0,para
cos
,para
1, 2, 3, …
é par, enquanto
0, 1, 2, 3, …
5.7
Similarmente, se é ímpar, então:
a
0,para
0, 1, 2, 3, …
5.8
54
2
1, 2, 3, …
Assim, a expansão para uma função secionalmente contínua muito suave por partes
é:
∑
a
2
a
E
∑
2
a cos
sen
Agora 5.9 só usa os valores de
toda função
≤
(5.9)
⇒
(5.10)
sen
entre
0 e
. Portanto para
dada sobre este intervalo, forma a série 5.9 . Esta é chamada a série de
Fourier Cossenos de
0≤
cos
⇒
. Segue que a série de Fourier convergirá para
e fora deste intervalo para a função periódica que coincide com
no intervalo
em 0 ≤
≤ . Por um caminho análogo, 5.10) define a série de Fourier Senos para uma função
( ) definida apenas entre 0 e . Esta série representa uma função periódica impar que
coincide com ( ) em 0
.
55
CONCLUSÃO
É possível partir de uma ideia, de uma vontade conseguir atingir uma meta, partindo de
conceitos preliminares, edificar o produto final com definições, demonstrações complexas e
construir um trabalho digno dos melhores assim essa monografia foi realizada.
Começando de definições elementares como periodicidade, ciclo trigonométrico, função
seno, cosseno, tangente, função par e impar e suas integrais correspondentes e usando
proposições, estas todas demonstradas no trabalho e culminando seu ápice. Devido a necessidade
de compreensão de áreas afins procura-se neste descrever e fazer a diferença entre frequência e
frequência angular muito úteis em aplicações eletromagnéticas por exemplo.
Para introduzir as séries trigonométricas fez-se um histórico mostrando todas as séries e
seus coeficientes por Jean Batiste Joseph Fourier (1768-1830), esses assuntos vinculados em seu
livro “Teoria Matemática de Condução do Calor”. Empregando os conceitos de funções
ortogonais, determina também os coeficientes de Fourier e aplicando as identidades
trigonométricas para resolver as integrais necessárias para instituir os mesmos coeficientes,
porém de outra maneira, depara-se os valores de a , a
. A continuidade e a convergência
das Séries de Fourier são corroboradas através de vários teoremas e alguns corolários. Inclusive
da própria série para funções continuas, onde depara com os problemas de funções
seccionalmente contínuas por partes suaves, muito suaves e com saltos. Até, encontrar funções
que apresentam cantos e é desenvolvida uma teoria para instruir os menos capacitados para o
assunto em pauta.
Foram feitas aplicações utilizando esta fundamentação para tornar transparente e claro
este tema tão fascinante e importante em muitas áreas das Ciências Exatas e da Terra. Sendo
prepara a expansão de Série de Fourier para fora do intervalo dado e mostrando a convergência
usando o método do erro quadrático mínimo dentro do intervalo dado.
Um detalhe imprescindível é que este Trabalho de Conclusão de Curso (TCC) procura
estabelecer uma relação teórica com sua praticidade e para tal é manipulado um software
56
denominado MATLAB que é um laboratório de matrizes, utilizando uma linguagem e um
sistema interativo de programação com facilidades de gerar gráficos e torna a interface homem
máquina muito fácil, por esta razão vem sendo adotado nas áreas tecnológicas do Brasil e do
mundo.
57
BIBLIOGRAFIA
[1] FIGUEIREDO, Djairo Guedes. - Análise de Fourier e Equações Diferenciais Parciais.
Rio de Janeiro, IMPA, Projeto Euclides, 1977.
[2] GUIDORIZZI, Hamilton Luiz, Um Curso de Cálculo - vol. 1, Livros Técnicos e
Científicos Ed., 1997.
[3] HANSELMAN D., B. Littlefield. MATLAB 6 -- Curso Completo. Pearson Education
do Brasil, 2003.
[4] IEZZI, Gelson. Fundamentos da Matemática Elementar – Conjuntos e Funções. Vol. 1,
Vol. 3. São Paulo: Atual, 1998.
[5] KAPLAN, Wilfred Advanced Calculus, Fifth Edition. Wilfred Kaplan. Publishing
House of Eletronics Industry.
[6] KIUSALAAS, Jaan. Numerical Methods in Engineering with
.
Cambridge University Press.
[7] LITTLEFIELD, Bruce e HANSELMAN, Duane.
Curso Completo.
Editora Prentice Hall. São Paulo, 2003.
[8] MATLAB, The Language of Technical Computing - Version 5.0.0.4069, License
number 108479 Pcruz, 1996.
[9] MORAES, Pedro Cruz. Dicas e Truques do
– Apostila. Belém-Pa., 2010.