Revisão Matemática - Instituto de Física

INSTITUTO DE FÍSICA UFRGS
FÍSICA IIC (FIS01182)
Método Keller
UNIDADE II
VETORES E INTEGRAIS
I. Introdução :
Na Unidade I você tomou conhecimento de alguns conceitos importantes, tais como
elétrica , condutores
e
isolantes , conservação
e
quantização
carga
da carga elétrica, bem como aprendeu
a calcular forças elétricas entre cargas puntiformes.
Nesta Unidade, no entanto, vamos nos afastar um pouco do conteúdo propriamente dito da
disciplina, de modo a fazer uma revisão matemática que proporcionará um melhor rendimento no
resto do curso. A razão para isto é muito simples.
É certo que, quanto mais nos aprofundamos nos estudos dos fenômenos físicos, para que possamos estudálos e representálos analiticamente, mais conhecimento matemático necessitamos ter.
A experiência nesta disciplina tem demostrado que os alunos têm muita diculdade no curso, e às
vezes até desistem de fazêlo, devido a problemas com a Matemática, principalmente pelo enfoque
diferente com que ela é aplicada à Física. Por esta razão, nesta Unidade procuraremos explorar,
de um ponto de vista puramente prático, alguns tópicos sobre vetores e integrais, atacando apenas
os pontos relevantes ao nosso curso de Eletromagnetismo.
O conteúdo desta Unidade II iniciase com as usuais denições de grandezas escalares e vetoriais, bem como com as operações vetoriais mais necessárias ao curso. A seguir, é apresentada
uma revisão de Cálculo Integral, abordando integrais indenidas e denidas de funções escalares, culminando com a reapresentação do Teorema Fundamental do Cálculo Integral.
Algumas
aplicações envolvendo técnicas de integração, bem como aplicações destas técnicas na obtenção
de momentos de inércia de distribuições contínuas de massa são exemplicadas. Estes exemplos
servem de guia para o cálculo de campos elétricos e magnéticos que surgirão durante o curso, a
partir da próxima Unidade. Observe que resolução de problemas envolvendo integrais será uma
atividade comum daqui para frente, não só nesta disciplina como nas que virão após. Portanto,
você tem agora uma boa oportunidade de adquirir prática na aplicação de seus conhecimentos
neste assunto.
Para nalizar, apresentamos um tópico sobre integração de vetores, que inclui a integração
ordinária de vetores, integrais de linha , de superfície e de volume. Você já teve contato com os
dois primeiros tipos de integração, uma vez que na Física I, o cálculo do
uma força variável ,
trabalho realizado por
nos casos uni e bidimensionais, é feito com estes 2 tipos de integrais.
Se você der especial atenção a esta Unidade e atingir plenamente todos os objetivos propostos
a seguir, seu curso de Física II será bastante facilitado e você poderá concentrar seus esforços na
Física propriamente dita, pois a bagagem matemática necessária para o curso está contida aqui.
Na próxima Unidade retornaremos ao livrotexto.
1
II. Objetivos :
Ao término desta unidade você deverá ser capaz de:
1)
2)
3)
somar vetores pelos métodos geométrico e analítico;
4)
5)
6)
7)
resolver integrais pelo
culo;
escalar e vetorial entre dois vetores;
integral indenida e integral denida , e aplicar
calcular os produtos
conceituar
calcular
o
Teorema Fundamental do Cál-
método de substituição de variáveis ;
momentos de inércia de distribuições lineares contínuas
conceituar integrais duplas e triplas;
resolver integrais ordinárias de vetores e conceituar
volume .
de massas;
integrais de linha, de superfície
e
de
III. Procedimento sugerido :
a) Leia o texto
Tópicos de Análise Vetorial
em anexo e resolva os exercícios nele
contidos.
b) Leitura aconselhada: Cap. 3 do Livrotexto : Fundamentos de Física, D. Halliday,
a
R. Resnick e J. Walker, vol. 1, 4 ed., LTC, 1996.
IV Respostas dos exercícios do texto:
Seção 2
35, 5 km; (b) 23, 7o .
4) (a) 6ı̂ − 3̂ − 3k̂ ; (b) −̂ + k̂ ; (c) ̂ − k̂ .
√
5) s =
a2 + b2 + 2 ab cos θ. 6) Sim. 7) Não. Sim.
9) (a) 1 nos três casos; (b,c) 0 nos três casos; (d) k̂ , ı̂ e ̂;
10) (a) 13; (b) 3(ı̂ + ̂ + k̂) (c) −3(ı̂ + ̂ + k̂).
~B
~
Ax Bx +Ay By +Az Bz
A·
√ 2 2 2.
11) cos θ = ~ ~ = √ 2
2
2
1) Não. Sim.
2) Não.
|A||B|
12)
3) (a)
Ax +Ay +Az
(e)
Bx +By +Bz
21, 8o .
Seção 3
√
ln L+a
,
b.
R2 + a2 − a, c. a1 − √R21+a2 ,
a
Iz = ρa3θo . 3) I = 35 ρa3 . 4) I = 3πρa3 .
l2
Iz = ρL 12
+ r2 . 6) I = 43 ρL3 .
1) a.
2)
5)
Seção 4
1)
2)
~ = 11, 7.
I~ = 8ı̂ + 8, 6̂; |I|
~ = 0.5.
I~ = 0, 5k̂ ; |I|
2
d.
1
.
2
−̂, −k̂
e
−ı̂.
Tópicos de Análise Vetorial
No estudo da eletricidade e do magnetismo grande economia de notação e grande clareza
podem ser obtidas se usarmos a notação da
análise vetorial .
O propósito desta Unidade é dar
uma breve, mas consistente, exposição (ou revisão, para aqueles que já estão familiarizados com
o assunto) da análise vetorial básica e fornecer o conhecimento necessário para um melhor e mais
adequado tratamento para a eletricidade e magnetismo.
1 Grandezas:
No estudo da Física elementar, muitos tipos de grandezas foram encontradas. Em particular,
a separação entre
escalares
e
vetores
foi feita e nos é suciente. Vejamos estas denições:
1.1 Escalares:
Um escalar é uma grandeza que ca completamente caracterizada por sua magnitude . Exemplos de escalares são muitos: massa, tempo, área , etc.
Uma extensão simples do conceito de escalar é o de campo escalar , i.e., uma função da posição
que é completamente especicada por sua magnitude em todos os pontos no espaço, como por
exemplo a
temperatura
de uma sala: ela pode ser diferente em diferentes pontos da sala. Outro
potencial eletrostático .
exemplo, e que nos interessará em muito, é o do
1.1 Vetores:
Um vetor é uma grandeza que é completamente caracterizada por sua magnitude, direção e
sentido. Como exemplos de vetores podemos citar a posição desde uma origem xa, velocidade ,
aceleração , força , etc. Usualmente os vetores são representados gracamente por uma echa cujo
comprimento é proporcional a magnitude do vetor, a direção é a reta que passa ao longo da mesma
e o sentido é dado pela orientação da echa, indicada por sua ponta.
No texto, os vetores são
representados ou por uma letra em negrito ou por uma letra com uma pequena echa em cima.
A generalização para um
campo vetorial
fornece uma função de posição que ca completamente
especicada por sua magnitude, direção e sentido
em todos os pontos do espaço .
O
campo elétrico ,
que será estudado na Unidade seguinte é um exemplo de campo vetorial.
2 Álgebra Vetorial:
Uma vez que a álgebra de escalares já é familiar a você, a usaremos para desenvolver a álgebra
vetorial. Para que isto possa ser efetivado, vamos começar representando os vetores em uma forma
mais conveniente.
2.1 Decomposição de vetores:
Consideremos um sistema de coordenadas cartesiano tridimensional. Este sistema será denotado pelas três variáveis
x, y e z
direção ao eixo
y
(ou
x2 ),
x1 , x2 e x3 . O sistema deve ser dextrógiro ,
x1 ) e a girarmos (pelo menor ângulo) em
alinhado com o eixo z (ou x3 ).
ou, quando convier, por
i.e., se alinharmos a palma da mão direita ao eixo
x
(ou
o polegar esticado deve car
3
V~
Com relação a este sistema, um vetor
por suas componentes cartesianas
Vx , Vy
é especicado
e
Vz
tais que
Vx = |V~ |cos αx
Vy = |V~ |cos αy
Vz = |V~ |cos αz
onde
|V~ |
é o módulo do vetor
V~
e
(1)
αi
é o ângulo entre
campo vetorial , cada
componente deve ser interpretada com uma função de x,
y e z . A Fig.1 ao lado mostra o vetor V~ com suas res
o vetor e o eixo
i.
No caso de um
Fig.1
Decomposição do vetor V~ em
componentes cartesianas Vx , Vy e Vz .
pectivas componentes. Deve ser enfatizado que introduzimos a representação dos vetores segundo
um sistema de coordenadas cartesiano apenas por simplicidade e para facilitar o entendimen-
Todas as denições e operações são, de fato, independentes de qualquer escolha especial de
coordenadas .
to.
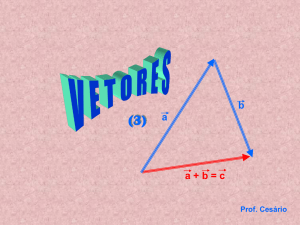
2.2 Soma de vetores:
A soma de dois vetores é denida como o vetor
pondentes componentes dos vetores originais .
~,
B
cujas componentes são as somas das corres-
Assim, se
~
C
é o resultado da soma dos vetores
~
A
e
escrevemos
~ =A
~ + B
~
C
(2)
e
Cx = Ax + Bx ,
Cy = Ay + By
Cz = Az + Bz .
e
(3)
soma vetorial é completamente equivalente
regra do paralelogramo para a adição vetorial, que
Esta denição de
à conhecida
está indicada na Fig. 2 ao lado.
subtração vetorial é denida em termos do negativo de um
vetor, que é um vetor cujas componentes são as negativas das
A
correspondentes do vetor original. Assim, se
~
A
é um vetor,
~
−A
é denido por
Fig.2
~ x = −Ax ,
(−A)
~ y = −Ay
(−A)
e
~ z = −Az .
(−A)
(4)
Soma vetorial usando a
regra do paralelogramo .
A operação de subtração é então denida como a soma do negativo, i.e.,
~ − B
~ =A
~ + (−B)
~ .
A
Como a soma de números reais é
associativa .
(5)
associativa , seguese que a adição vetorial (e subtração) é também
Em notação vetorial
~ + (B
~ + C)
~ = (A
~ + B)
~ +C
~ = (A
~ + C)
~ +B
~ =A
~+B
~ +C
~ .
A
Em palavras,
os parênteses não são necessários ,
(6)
como indicado pela última expressão.
2.2 Multiplicação de vetores:
O mais simples produto é aquele de um
escalar por um vetor .
Esta operação resulta num
vetor cujas componentes são dadas pelo produto da multiplicação do escalar pela correspondente
4
componente do vetor original. Se
~ um vetor,
c é um escalar e A
o produto
~ é o vetor B
~,
cA
denido
por
Bx = cAx ,
Fica claro que, se
vetorial
que
não é
~ for um campo vetorial
A
By = cAy
e
e
Bz = cAz .
(7)
~
c for um campo escalar , então B
será um
novo campo
necessariamente um simples múltiplo do campo original.
Agora, se desejamos multiplicar dois vetores, existem duas possibilidades, conhecidas como
produto escalar
produto vetorial .
Vamos considerar primeiro o produto escalar . Observe que o nome do
~·B
~. é
natureza escalar do produto. A denição do produto escalar , escrito A
e
produto decorre da
~·B
~ = Ax Bx + Ay By + Az Bz .
A
(8)
Esta denição é equivalente a outra, talvez mais comum,
~·B
~ = |A||
~ B|
~ cos φ ,
A
onde
O
de
~
A
φ
é o ângulo entre os dois vetores (veja Fig.3 abaixo).
produto vetorial
e
(9)
~,
B
então
de dois vetores é um vetor, como o nome indica. Se
~ =A
~×B
~
C
~
C
é o vetor produto
ou, em componentes,
Cx = Ay Bz − Az By ,
Cy = Az Bx − Ax Bz
e
Cz = Ax By − Ay Bx .
(10)
é perpendicular ao plano que contém os dois vetores do produto e é
Esta denição mostra que o vetor
~
C
equivalente à seguinte denição:
~ = |A||
~ B|
~ sen ϕ ,
|C|
com o sentido dado pela
(11)
regra da mão direita
(a mesma
usada anteriormente para denir o sistema de coordenandas dextrógiro). A Fig.3 ao lado mostra a geometria
do produto vetorial. É importante notar que
Fig.3
o produto
Produto vetorial entre dois veto-
~ é determinado
res. O sentido do vetor C
vetorial depende da ordem dos fatores : intercambiando
a ordem dos vetores introduzimos um sinal negativo no
pela regra da mão direita .
resultado.
O produto vetorial pode ser facilmente obtido em termos de um
vetores unitários (i.e., possuem módulo 1) que denem as direções
determinante .
x, y
e
z,
Sejam
ı̂, ̂
e
k̂
respectivamente, do
sistema de coordenadas escolhido. Então,
ı̂
̂
k̂ ~×B
~ = Ax Ay Az .
A
Bx By Bz (12)
2.4 Exercícios:
1) Podese combinar dois vetores de módulos diferentes para que se tenha uma resultante nula?
E três vetores?
2) Pode um vetor ter módulo nulo se uma de suas componentes não o é?
5
30 km no sentido oesteleste; a seguir percorre 10 km no
o
sentido sulnorte e nalmente percorre 5 km numa direção que forma um ângulo de 30 com o
o
norte e 60 com o leste. (a) Use um sistema cartesiano de coordenadas e calcule o módulo do
3) Um carro percorre uma distância de
deslocamento resultante. (b) Obtenha o ângulo entre o vetor deslocamento resultante e o sentido
oesteleste.
4) Dois vetores são dados por
~a = 3ı̂ − 2̂ − k̂
e
~b = 3ı̂ − ̂ − 2k̂ .
Calcule: (a)
~a + ~b,
(b)
~a − ~b,
(c)
−~a + ~b.
5) Dois vetores de módulos
a
e
b
formam entre si um ângulo
θ.
Determine o módulo
s
do vetor
resultante da soma destes dois vetores.
6) Pode um produto escalar ser uma grandeza negativa? Explique.
7) Se
~×B
~ = 0
A
~
A
concluise que
e
~
B
são paralelos um ao outro?
A recíproca é verdadeira?
Explique.
~a: (a) ~a · ~a = a2
ı̂, ̂ e k̂ . Calcule:
8) Mostre que para qualquer vetor
9) Considere os vetores unitários
ı̂ · ı̂, ̂ · ̂ e k̂ · k̂
ı̂ × ı̂, ̂ × ̂ e k̂ × k̂
a)
c)
b)
d)
e (b)
~a × ~a = 0.
ı̂ · ̂, ̂ · k̂ e k̂ · ı̂
ı̂ × ̂, ̂ × k̂ e k̂ × ı̂
e)
ı̂ × k̂, ̂ × ı̂
e
(13)
k̂ × ̂
~a e ~b do problema 4), calcule: (a) ~a · ~b, (b) ~a × ~b, (c) ~b × ~a.
~ eB
~ têm componentes, segundo três eixos ortogonais x, y e z , dadas
11) Dois vetores A
~eB
~.
Ay e Az e Bx , By e Bz , respectivamente. Calcule o ângulo formado por A
12) Para os vetores ~
a e ~b do problema 4), calcule o ângulo que eles formam entre si.
10) Para os vetores
por
Ax ,
3 Cálculo Integral:
3.1 Integrais indenidas:
integral
dF (x)
= f (x), é chamada de
dx
de f (x). É claro que se F (x) é integral indenida de f (x), então F (x) + C , onde C é
d
uma constante qualquer, também é integral indenida de f (x), pois
(F (x) + C) = dFdx(x) = f (x).
dx
Logo,
.
Dada uma função
indenida
f (x),
qualquer função
F (x),
tal que
a integral indenida de uma função é determinada a menos de uma constante arbitrária
Simbolicamente, a integral indenida de
Z
f (x)
é representada por
f (x) dx = F (x) + C .
(14)
3.2 Integrais denidas:
Como você deve estar lembrado do seu curso de Cálculo, a
geometricamente
levantadas em
através da área limitada por uma curva
x=a
e
x=b
integral denida
y = f (x),
pode ser conceituada
o eixo dos
x
e as ordenadas
(veja Fig.4 a seguir). No entanto, a denição pode ser dada sem o
a ≤ x ≤ b em n subintervalos por meio dos pontos x1 ,
x2 , ... , xn−1 , escolhidos arbitrariamente. Em cada um dos novos intervalos (a, x1 ), (x1 , x2 ), ...
,(xn−1 , b) escolha arbitrariamente um ponto interno; tais pontos podem ser ξ1 , ξ2 , ...,ξn . Agora
uso da geometria. Subdivida o intervalo
execute a soma
f (ξ1 )(x1 − a) + f (ξ2 )(x2 − x1 ) + . . . + f (ξn )(b − ξx ).
6
Chamando
e
xk − xk−1 = ∆k ,
f (ξk ) ∆k ,
(15)
a = xo , b = xn
a soma pode ser reescrita
n
X
k=1
que, geometricamente, representa a soma das
área dos retângulos mostrados na Fig.4. Consideremos agora que o número de subdivisões,
∆xk → 0.
aumente de tal forma que cada
n,
As-
sim, a soma (15) se aproxima de um limite cujo
valor
não depende do modo de subdivisão
Subdivisão da área sob a curva em elementos ∆k .
Fig.4
e, ge-
y = f (x) mostrada
pontos a e b como
ometricamente, se torna idêntico à área sob a curva
denir a
integral denida
f (x),
da função
n
X
lim
∆xk →0
Do lado direito desta equação,
integração .
f (x)
entre os
f (ξk ) ∆k =
k=1
é chamada de
Z b
na Fig.4. Podemos então
f (x) dx .
(16)
a
integrando
e
a
e
b
são chamados de
limites de
3.3 Algumas propriedades das integrais denidas:
1.
2.
Z b
a
Z b
3.
a
Z c
4.
Z b
{f (x) ± g(x)} dx =
A f (x) dx = A
5.
a
f (x) dx ±
f (x) dx , A
Z b
g(x) dx ,
(17)
a
sendo uma constante qualquer
,
(18)
a
f (x) dx =
Z b
f (x) dx +
f (x) dx = −
Z c
f (x) dx ,
(19)
b
a
a
Zaa
Z b
Z b
Z a
f (x) dx ,
(20)
b
f (x) dx = 0 .
(21)
a
3.4 Teorema fundamental do Cálculo Integral:
Se
F (x)
é a integral indenida de
f (x),
Z b
a
então
f (x)dx = F (b) − F (a) .
(22)
Este importante teorema permite-nos calcular as integrais denidas sem o uso direto de sua denição, sempre e quando a integral indenida seja conhecida.
3.5 Algumas integrais imediatas:
A seguir apresentamos as integrais indenidas de algumas funções simples. Para os propósitos
do nosso curso, você deverá saber de cor pelo menos as sete primeiras.
1.
R
un du =
un+1
n+1
, n 6= −1 2.
7
R du
u
= ln|u|
(23)
3. R sen u du = −cos u
5. R sec2 u du = tg u
7. eu du = eu
R
−1 u
−1 u
9. √adu
ou cos
2 −u2 = sen
a
a
R
1 −1 u
11. u2du
=
tg
2
+a
a
a R
13. u√udu2 −a2 = a1 cos−1 ua
R
R
4. R cos u du = sen u
6. R cosec2 u du = −cotg u
u
8. au du = lna u , a > 0 , a 6= 1 √
R
10. √udu
u2 ± a2
2 ±a2 = ln u ±
R du
1
12. u2 −a2 = 2a
ln u−a
u+a
(24)
3.6 Método de substituição de variáveis:
Se o cálculo de uma integral
R
f (x)dx
não é imediatamente óbvio em termos das formas ime-
diatas anteriores, em muitos casos ela pode ser resolvida substituindose a variável
u(x),
variável conveniente,
ja uma integral imediata.
integração ,
de tal modo que a integral resultante em termos de
Neste método,
que na nova forma integral,
R
u,
R
x por uma
g(u)du, se-
cuidado especial deve ser tomado com os limites de
g(u)du,
devem ser expressos em termos de
Vamos ilustrar o método através de dois exemplos:
R L dx
0 (x+a)2 fazendo a substituição x
Então: x = u − a → dx = du.
Exemplo 1: Calcule
u.
+ a = u.
Para os limites de integração temos:
x=0 → u=a;
x=L → u=a+L ,
(25)
de modo que
Z L
0
onde usamos a integral imediata
Exemplo 2: Calcule
Então
a+L
Z a+L
u−1 dx
du Z a+L −2
=
=
u
du
=
2
2
(x + a)
u
−1 a
a
a
2
R∞
0
dx = a sec θdθ
e
=
1
1
L
−
=
,
a a+L
a(a + L)
(26)
1.
dx
fazendo a substituição x
(x+a)3/2
2
2
2
2
2
2
= a tgθ.
x + a = a (1 + tg θ) = a sec θ, e os limites
de integração
x=0 → θ=0;
π
x=∞ → θ= .
2
(27)
A integral se torna então
Z ∞
0
π
Z π
2
π
dx
1
1 Z 2
1
2 a sec θ dθ
=
=
cosθ dθ = 2 [senθ]02 = 2 .
3/2
3
3
2
(x + a)
a sec θ
a 0
a
a
0
(28)
3.7 Aplicação cálculo do momento de inércia de um o:
O cálculo do momento de inércia de um o homogêneo (de densidade linear de massa constante)
é um tipo de problema que envolve a montagem e resolução de integrais numa forma muito
semelhante aos problemas de cálculo de campos elétricos e magnéticos que abordaremos em nosso
curso, com a vantagem de incluir apenas grandezas que já são do seu conhecimento.
8
a)
Momento de inércia de um ponto material :
o momento de inércia de um ponto material de
massa
m,
z,
como você deve
2
estar lembrado da Física I, é denido por Iz = r m,
onde
r
em relação a um eixo
é a distância do ponto ao eixo (veja Fig.5
ao lado).
Fig.5
Massa m distante r do eixo de rotação z .
Fig.6
Massa mi distante ri do eixo de rotação z .
b) Momento de inércia de uma distribuição dis
creta de pontos materiais , em relação a um eixo
z,
é a soma dos momentos de inércia de cada
ponto com relação ao mesmo eixo
Iz =
n
X
z,
i.e.,
ri2 mi ,
(29)
i=1
conforme a Fig.6 ao lado.
c) Momento de inércia de uma distribuição contínua e linear de massa :
considere
uma
distri-
buição contínua de massa, ou seja, um o com
densidade linear de massa , ρ, constante.
calcular
o
momento
relação a um eixo
z
de
inércia
Podemos
deste
o
com
dividindo o o em pedaços de
dl,
dm = ρ dl,
comprimentos innitesimais,
que contêm uma
massa innitesimal
e que, portanto,
podem
ser
materiais .
tratados
como
pontos
verdadeiros
Fig.7
Fio homogêneo rotando em torno do eixo z .
Desta forma, o momento de inércia de cada um destes pedaços innitesimais é, de acordo com
o item a) acima,
dIz = r2 dm = r2 ρ dl .
(30)
Finalmente somamos todos os momentos de inércia devidos a cada um dos elementos
dl
de que se
compõe o o. Numa notação pouco rigorosa podemos escrever
Iz =
X
dIz =
X
r2 dm .
(31)
No entanto, se considerarmos a distância de um ponto do o ao eixo,
do ponto sobre o o,
l,
r,
como função da posição
(ou viceversa), a soma da expressão acima é a soma dos produtos dos
dl, em que foi dividido o intervalo total de denição de uma função, pelos
2
desta função, r , em cada um daqueles intervalos innitesimais. Portanto esta
intervalos innitesimais,
respectivos valores
soma é, rigorosamente falando, uma integral,
Iz =
Z
dIz =
Z
r2 dm = ρ
Z
r2 dl ,
(32)
cujos limites de integração devem abranger o comprimento total do o.
R 2
É claro que para podermos calcular a integral
r dl temos que explicitar a relação funcional
entre
r
e
dl,
ou substituindo
r
em função de
l
ou ambas em função de uma terceira variável.
9
Exemplo 3:
Calcule o momento de inércia do
segmento da Fig.8, de densidade linear de massa
y
e (b) em
x2 dl .
(33)
constante: (a) em relação ao eixo dos
x.
relação ao eixo dos
(a) Temos
Iy =
Como
x
Z
x2 dm = ρ
Z a+L
Fig.8
a
é o mesmo para todos os
Iy = ρb
2
Z a+L
Segmento de o de comprimento L.
dl (x = b)
dl = ρb2 L .
(34)
a
(b) Agora
Z
Ix =
2
y dm = ρ
Z a+L
y 2 dl .
(35)
a
A integral nesta forma não pode ser resolvida, pois aparecem nela duas variáveis interdependentes.
Temos que expressar
y
em função de
l
ou viceversa. Vemos imediatamente que
dl = dy ,
pois a
segmento de reta é paralelo ao eixo dos y. Assim,
Ix = ρ
Exemplo 4:
2
y dy =
a
a+L
y3 ρ 3
1
= ρ[(a + L)3 − a3 ] .
3
a
(36)
Calcule o momento de inércia de
um o em forma de
a,
Z a+L
1/4
de circunferência de raio
ρ,
em relação
x2 dl .
(37)
de densidade de massa uniforme
a um de seus diâmetros.
De acordo com a Fig.9 ao lado,
Iy =
Z
x2 dm = ρ
Z
Neste caso o mais simples é expressar tanto
x = a senθ
e
x
como
Fig.9
dl
Fio em forma de 1/4 de circunferência.
em função de
dl = a dθ , θ
θ
em radianos
.
(e de
dθ),
i.e.,
(38)
Esta integral pode ser resolvida facilmente através de uma transformação trigonométrica (faça
a!!), tendo como resultado
Iy = ρ a
3
"
θ sen 2θ
−
2
4
#π
2
0
=
π 3
ρa .
4
(39)
3.6 Integrais duplas:
f (x, y) uma função de duas variáveis livres denida numa região R do plano xy , conforme
indica a Fig.10 a seguir. Subdivida R em n sub-regiões ∆Rk , de área ∆Ak , k = 1, 2, ..., n. Sejam
(ξk , ηk ) as coordenadas de um ponto interno de ∆Rk .
Seja
10
Forme a soma
n
X
f (ξk , ηk ) ∆Ak .
(40)
k=1
Considere agora o limite
lim
n→∞
n
X
f (ξk , ηk ) ∆Ak ,
(41)
k=1
Fig.10
Área subdividida em elementos ∆Ak .
no qual o número de divisões aumenta indenidamente e as dimensões de cada
∆Rk
se aproximam
de zero. Este limite é representado pelos símbolos
Z
f dA
de
f (x, y)
Z Z
ou
R
e é chamado de
integral dupla
f (x, y) dx dy ,
(42)
R
sobre a região
R.
3.7 Integrais triplas:
Os conceitos anteriores podem facilmente ser generalizados para regiões tridimensionais. Considere uma função de 3 variáveis livres
a região em
n
f (x, y, z), denida numa região tridimensional R.
∆Vk , k = 1, 2, ..., n. Chamando de (ξk , ηk , ρk )
subregiões de volume
Subdivida
um ponto
interno de cada subregião, forme o limite da soma
lim
n→∞
n
onde o número
n
X
f (ξk , ηk , ρk ) ∆Vk ,
(43)
k=1
de subdivisões tende ao innito, de modo que as dimensões das subregiões
tendem a zero. Se este limite existe, ele é denotado por
Z
f dV
ou
R
e é chamado de
Z Z Z
R
f (ξk , ηk , ρk ) dx dy dz ,
integral tripla de f (x, y, z) sobre R.
de massa (variável) da região
R,
Por exemplo, se
(44)
f (x, y, z) descrever a densidade
a integral acima dará a massa total da região.
3.8 Exercícios:
1) Calcule as seguintes integrais usando o método de substituição de variáveis e a lista das
integrais imediatas:
a.
Z L
0
Z R
Z R
Z π
dx
x dx
x dx
2
√
; b.
; c.
; d.
senθ cosθ dθ .
2
2
3/2
2
2
x+a
0
0 (x + a )
0
x +a
2) Calcule o momento de inércia de um o em
forma de arco de circunferência de raio
central
θo
a,
ângulo
(veja Fig.11 ao lado) e densidade linear
de massa constante
ρ,
em relação ao eixo
z
per-
pendicular ao plano do arco que passe pelo centro
do mesmo.
Fig.11
11
Fio em forma de arco.
(45)
3) Calcule o momento de inércia de um o homogêneo em forma de circunferência completa de
raio
a,
ρ,
com densidade linear de massa uniforme
em relação a um eixo tangente a circunferência
e situado no mesmo plano desta.
4) Calcule o momento de inércia de um o retilíneo homogêneo com densidade linear de massa
uniforme
xo
z
ρ
e comprimento
L,
em relação a um ei-
perpendicular ao plano da página e situado a
uma distância
R
do o, confrome mostra a Fig.12
ao lado.
Fig.12
Fio homogêneo rotando.
5) Usando o resultado do problema 4), calcule o momento de inércia de um o com as mesmas características daquele, dobrado em forma de quadrado de lado
L,
em relação a um eixo
perpendicular ao plano do quadrado que passa pelo centro do mesmo.
4 Integração de Vetores:
Até o momento consideramos apenas integrais de funções escalares, i.e., funções cujos valores
são números.
A Fig.13 ao lado representa os valores de um
F~ (x, y, z) em dois pontos do espaço, (x1 , y1 , z1 ) e (x2 , y2 , z2 ). um exemplo de camcampo vetorial
po vetorial pode ser
F~ (x, y, z) = 2yı̂ + (x2 + y)̂ + z 2 k̂ .
cujo valor no ponto
2ı̂ + ̂ + 4k̂ .
(46)
(0, 1, 2), por exemplo, é o vetor
Vamos agora considerar campos vetoFig.13
riais ou funções vetorias, cujos valores são vetores.
Campo vetorial.
4.1 Integrais ordinárias de vetores:
Os campos ou funções vetoriais são passíveis de integração de modo inteiramente análogo às
funções escalares. Porém, cuidados especiais devem ser tomados devido ao caráter vetorial destas
funções. Consideremos, por simplicidade, uma função vetorial que depende apenas da coordenada
x,
por exemplo
F~ (x) = Fx (x)ı̂ + Fy (x)̂ + Fz (x)k̂ .
(47)
A integral
I~ =
Z b
F~ (x) dx
(48)
a
representa, do mesmo modo que para as funções escalares, a soma dos produtos dos intervalos
dx em que se divide o intervalo total [a, b] de denição da função F~ (x), pelos valores
~ (x) é um vetor, esta
desta função naqueles intervalos innitesimais. Porém, como F
innitesimais
respectivos
soma é uma
soma vetorial
e não uma soma de números, e o seu resultado é um
número. Esta importante observação quer dizer que
12
não podemos
vetor,
e não um
simplesmente integrar o módulo
de
F~ (x)
para obter o módulo da integral, porque o módulo de uma soma de vetores não é igual à
soma dos módulos dos vetores, i.e.,
Z b
I 6=
mas que temos que decompor
a
|F~ (x)| dx ,
(49)
F~ (x) em suas componentes e integrar cada uma delas separadamente
para obter as componentes correspondentes da integral,
I~ =
Z b
Z b
F~ (x) dx =
a
a
Fx (x) dx ı̂ +
Z b
a
Fy (x) dx ̂ +
Z b
a
Fz (x) dx k̂
= Ix ı̂ + Iy ̂ + Iz k̂ ,
com
I=
(50)
q
Ix2 + Iy2 + Iz2 .
Três outros tipos de integrais vetoriais serão importantes em nosso curso.
Com isto quere-
mos dizer que será importante saber claramente o signicado destas integrais, embora não seja
importante saber como resolvêlas.
4.2 Integrais de linha:
Considere uma função vetorial
F~ (x, y, z)
das coordenadas or-
togonais x, y e z , que assume diferentes valores ao longo da curva
C , que vai do ponto A até o ponto B , conforme mostra a Fig.14.
Divida esta linha em n segmentos ∆lk , e a cada um deles associe
um vetor ∆~
lk (k = 1, 2, ..., n), com módulo ∆lk , cuja direção é a
do segmento e seu sentido é de A para B . Faça o produto escalar
de cada vetor ∆~
lk pelo valor de F~ num ponto deste segmento e
some todos os n produtos escalares.
A
integral de linha
é então denida como o limite desta soma
quando o número de subdivisões tende ao
∞
Fig.14
Caminho de integração.
de tal modo que o tamanho de cada segmento tende
a zero. Esta denição pode ser compactamente escrita com
Z B
AC
F~ · d~l = n→∞
lim
n
X
F~i · ∆~li .
É importante notar que a integral de linha depende não apenas dos pontos extremos,
também da curva
C,
(51)
i=1
a
e
b,
como
i.e., do caminho, sobre a qual a integração é feita. Um exemplo conhecido
trabalho realizado por uma força que atua sobre uma partícula quando
ela se desloca entre dois pontos A e B ,
deste tipo de integral é o do
Z B
A
F~ · d~l = WAB ,
(52)
como você deve ter visto em Física I.
Se a curva
C
for fechada, a integral de linha receberá uma notação especial:
I
C
F~ · d~l .
13
(53)
4.2 Integrais de superfície:
Considere um campo vetorial
F~ (x, y, z)
deni-
do nos pontos do espaço e uma superfície de forma
qualquer,
S.
n elemen∆Sk (k = 1, 2, ..., n). As-
Divida esta superfície em
tos de superfície de áreas
socie a cada elemento da superfície um vetor que
representaremos por
~k ,
∆S
de módulo
∆Sk ,
de di-
reção perpendicular à superfície e de sentido adotado através da convenção: se a superfície
S
não
é plana, a convenção usual é de adotarse para o
Fig.15
vetor o sentido que vai da face côncava para a face
produto escalar
convexa da superfície (veja Fig.14). Tome o
∆Sk
num ponto do elemento de área
e some todos os
Superfície de integração.
de cada vetor
~k
∆S
pelo valor de
F~
n produtos escalares.A integral de superfície é
∞ de tal modo
então denida como o limite desta soma quando o número de subdivisões tende ao
que o tamanho de cada elemento de área tende a zero. Esta denição pode ser compactamente
escrita como
Z
S
~ = lim
F~ · dS
n→∞
n
X
~i .
F~i · ∆S
(54)
i=1
Muito importante em nosso curso serão as integrais de superfície tomadas sobre superfícies fechadas
de diversos formatos. Também neste caso, a integral recebe uma notação especial
I
S
~ .
F~ · dS
(55)
Quando a superfície é fechada, a convenção para o sentido dos vetores
sempre apontando
para fora
~k
∆S
é o de considerálos
da superfície.
4.3 Integrais de volume:
Se
κ
um escalar e
F~
é um vetor, então as duas
J=
Claramente
J
é um escalar e
~
M
Z
κ dV ,
e
V
integrais de volume
~ =
M
Z
que nos interessarão são
F~ dV .
é um vetor. Estas integrais são bastante familiares e não requerem
maiores detalhamentos.
4.4 Exercícios:
1) Calcule
2) Calcule
(56)
V
R
I~ = 13 F~ (x) dx, onde F~ (x) = 2xı̂ + x2 ̂. Calcule o módulo de I~.
Rπ
I~ = 02 F~ (θ) dθ, onde F~ (θ) = senθ cosθ k̂ . Calcule o módulo de I~.
14